Цилиндрические функции

Цилиндрические функции – общее название для специальных функций одного переменного, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, записанных в цилиндрических координатах. Наиболее распространенными из них являются функции Бесселя.

Функциями Бесселя первого рода 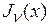и 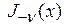называют функции, удовлетворяющие дифференциальному уравнению

,

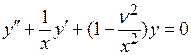называемому уравнением Бесселя. Функция Бесселя при 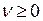представима в виде ряда следующим образом:

.

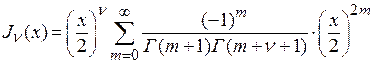В частности,

.

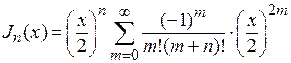Функции Бесселя с индексами, отличающимися на 1, связаны между собой следующим образом:

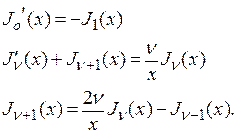
Функции Бесселя с четным показателем являются четными функциями, с нечетным показателем – нечетными.

Ниже приведены графики функций Бесселя для значений .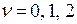

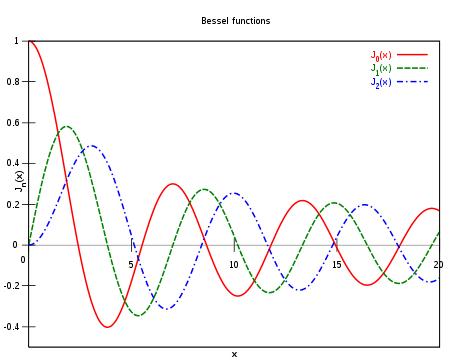
Графики функций Бесселя несколько напоминают графики синусов и косинусов, но с убывающей амплитудой. Каждая функция Бесселя имеет на вещественной полуоси бесконечное множество корней, достаточно равномерно распределенных по оси.

П р и м е р. Найти решение дифференциального уравнения

.

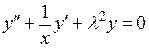Введем новое переменное: 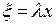. При этом обозначим 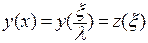. Теперь 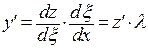, 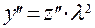. Поэтому уравнение в новых обозначениях принимает вид 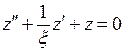. Это уравнение Бесселя при , следовательно, ограниченное в окрестности нуля решение этого уравнения – функция Бесселя нулевого порядка: 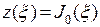. И значит, решением исходного уравнения является функция .

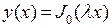Свойство ортогональности с весом функций Бесселя. Имеет место соотношени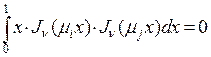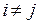е , , где 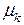– 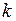-й (начиная с наименьшего) корень функции Бесселя 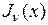. Мы докажем это свойство для 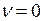. В общем случае доказательство аналогично.

Сначала введем в уравнении

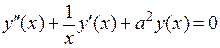
замены 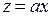, 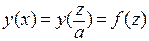. При этом получим 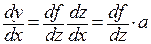, аналогично, 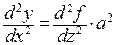. Поэтому уравнение примет вид 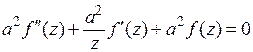или 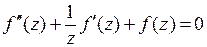, то есть, превратится в уравнение Бесселя нулевого порядка. Значит, 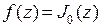. Таким образом, решением уравнения 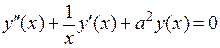является .

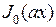Следовательно, 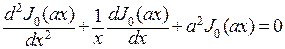и 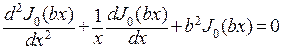. Умножим первое их этих равенств на 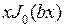и вычтем из результата второе равенство, умноженное на . Получим

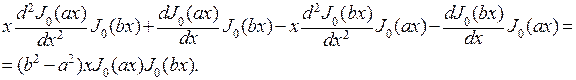
Левая часть последнего равенства примет вид

Таким образом, =.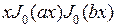

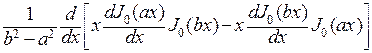Пусть теперь параметры 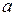и 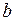– два различных корня функции 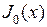. Проинтегрируем обе части предыдущего равенства по отрезку 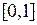. Получим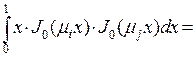 =0

Это равенство называется свойством ортогональности семейства 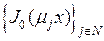на отрезке 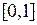. Применяя предельный переход и свойства функций Бесселя порядков, отличающихся на 1, можно доказать равенство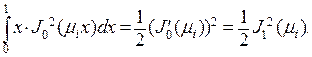

Дата добавления: 2014-01-14