Свойства вычислительных задач и алгоритмов

End.

Пример 1.5.

var x, b, s, h, s1, y: real;

i, n: integer;

begin {1-й блок}

x:= 0; s:= 0; b:= 10.7; h:= 0.01;

repeat s:= s + 1/(x – b);

x:= x + h;

until x >= b;

writeln('x = ',x,' s= ',s:10);

{2-й блок}

n:= round(b/h); s1:= 0;

for i:= 0 to n do

begin х:= i*h; s1:= s1 + 1/(х – b);

end;

writeln;

writeln('n= ',n,' х = ',х,' s1= ',s1:10);

readln;

В обоих блоках вычисляются значения функции 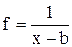на интервале [0, b] c шагом h = 0.01 при b = 10.7, и результаты суммируются. Теоретически оба результата должны быть равны ¥, т.к. , однако этого не происходит.

В первом случае изменение значения х происходит посредством его наращивания, т.е. с помощью оператора x:= x + h. При этом вследствие накопления ошибок округления, последнее значение х* превосходит 10.7 и составляет х*» 10.71. Во втором блоке используется более точная формула y:= i*h, при этом последнее значение у*» 10.7, т.е. “заступа” не происходит. За счет такого различия в методе изменения аргумента значения s и s1 отличаются даже знаком. В дальнейшем рекомендуем применять для изменения аргумента в цикле формулу второго типа.

Из особенности машинного представления вещественных чисел (типа Real), в частности из необходимости их округления, следует, что операция сравнения двух вещественных чисел по совпадению некорректна. Иными словами, применение оператора вида “if x = b then…” скорее всего, приведет к тому, что используемое в нем логическое выражение будет почти всегда ложно. По той же причине в обоих блоках примера 1.5. не происходит переполнения, поскольку ни одно из значений х* и у* не совпадает с b, хотя их точные значения х и у в конце цикла равны b. В тех же случаях, когда логика алгоритма требует проверки совпадения, рекомендуется использовать следующий оператор “if abs(x – b) <= eps then…”, где значение eps достаточно мало, но существенно больше машинного ипсилон. Например, можно положить eps:= 1.0e–6. Отметим, что сравнение по совпадению целых чисел (типа Integer) происходит корректно.

Будем считать, что постановка задачи включает в себя задание множества допустимых входных данных Х и множество возможных решений Y. Цель вычислительной задачи состоит в нахождении решения y ÎY по заданному входному данному xÎX. Предположим также, что для оценки величин погрешностей приближенных входных данных х* и приближенного решения у* введены абсолютные и относительные погрешности D(х*), D(у*), d(х*), d(у*).

Корректность задачи. Вычислительная задача называется корректной, если выполнены три требования:

1) её решение y ÎY существует при любом входном данном xÎX;

2) это решение единственно;

3) решение устойчиво по отношению к малым возмущениям входных данных.

Если хотя бы одно требование не выполнено, задача называется некорректной.

Решение y ÎY вычислительной задачи называется устойчивым по входным данным хÎY, если оно зависит от входных данных непрерывным образом. Иными словами, для любого e > 0 существует d = d(e) > 0, что всякому входному данному х*, удовлетворяющему условию D(х*) < d соответствует приближенное решение у*, для которого D(у*) < e. Таким образом, решение устойчивой вычислительной задачи теоретически можно найти со сколь угодно высокой точностью, если обеспечена достаточно высокая точность входных данных.

Приведем простейшие примеры устойчивых и неустойчивых задач.

Пример 1.6. Дано приведенное квадратное уравнение z² + pz + q = 0. Входными данными задачи (то, что выше обозначалось как x) являются значения коэффициентов р и q, (p, q) = x. Согласно сведениям из школьной алгебры, решения уравнения определяются по формулам

. (1.1)

Это выходные данные (z₁, z₂) = y. Очевидно, оба корня являются непрерывными функциями коэффициентов, следовательно, решение данной задачи устойчиво.

Пример 1.7. Решение задачи о вычислении ранга матрицы в общем случае неустойчиво. В самом деле, ранг матрицы 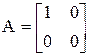равен 1, поскольку det A = 0 и в ней имеется ненулевой элемент. Однако сколь угодно малое возмущение элемента а₂₂ на величину e ¹ 0 приведет к невырожденной матрице , ранг которой уже равен 2.

Обусловленность задачи. Теоретически наличие у задачи устойчивости означает, что ее решение может быть найдено со сколь угодно малой погрешностью, если только гарантировать, что погрешности входных данных достаточно малы. Однако на практике погрешности входных данных не могут быть сколь угодно малыми, их точность ограничена. Даже то, что данные нужно вводить в ЭВМ, означает, что их относительная точность заведомо ограничена величиной порядка e_М. В реальности же уровень ошибок в исходной информации будет существенно выше. Как же повлияют малые, но конечные погрешности входных данных на точность решения? Для ответа на это вопрос введем понятие обусловленности.

Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных. Задачу называют хорошо обусловленной, если малым погрешностям входных данных отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения.

Пример 1.8. Имеем систему линейных уравнений:

.

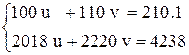Ее решение: u = 12.1; v = – 9.09. Округлим коэффициенты правой части до целых, получим систему

,

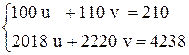решение которой: u = 1; v = 1. Видим, что незначительное искажение условий задачи сильно изменило решение, даже поменяло знаки, т.е. данная задача плохо обусловлена.

Другим примером плохо обусловленной задачи является уже знакомая задача вычитания приближенных чисел одного знака.

Часто оказывается возможным ввести количественную меру степени обусловленности задачи – число обусловленности. Эту величину можно интерпретировать как коэффициент возможного возрастания погрешности решения по отношению к вызывающим их погрешностям входных данных. Если между абсолютными погрешностями входных данных х и решения у установлено неравенство

D(у*) £ n_D ×D(х*),

то величина n_D называется абсолютным числом обусловленности. Если же выполняется неравенство

d(у*) £ n_d × d(х*),

то величина n_d называется относительным числом обусловленности.

Для плохо обусловленной задачи n_D >>1 и n_d >> 1. В некотором смысле неустойчивость задачи – это крайнее проявление плохой обусловленности, когда n = ¥.

Пример 1.9. Оценим величину обусловленности задачи вычисления определенного интеграла .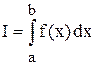

Пусть f*(x) – приближенно заданная подынтегральная функция, для которой справедлива оценка . Тогда

D(I*) = | I – I*| = £ (b – a) ×D(f*).

Полученное неравенство означает, во-первых, что задача вычисления определенного интеграла устойчива, т.к. для любого e > 0 неравенство D(I*) < e будет выполнено, если выполняется условие D(f*) < e / (b – a).

Во-вторых, полученное неравенство означает, что абсолютное число обусловленности задачи вычисления определенного интеграла равно n_D = (b – a).

Корректность алгоритмов. Вычислительный алгоритм называется корректным, если выполнены три требования:

1) он позволяет после выполнения конечного числа элементарных для вычислительной машины операций преобразовать любое входное данное xÎX в результат y ÎY;

2) результат устойчив по отношению к малым возмущениям входных данных;

3) результат обладает вычислительной устойчивостью.

Если хотя бы одно требование не выполнено, то будем называть алгоритм некорректным. Обсудим эти требования.

Требование устойчивости алгоритма по входным данным аналогично требованию устойчивости вычислительной задачи и означает, что при отсутствии вычислительной погрешности результат зависит от входных данных непрерывным образом.

Пример 1.10. Пусть алгоритм предназначен для вычисления вещественных корней приведенного квадратного уравнения z² + pz + q = 0 с коэффициентами, удовлетворяющими условию d = p² – 4q ³ 0. Если в нем используется формула (1.1), то этот алгоритм некорректен. В самом деле, значение d*, отвечающее приближенно заданным коэффициентам p* и q* может оказаться отрицательным, если d» 0. Тогда решение завершится аварийным остановом при попытке извлечь квадратный корень из отрицательного числа. Если же в формуле (1.1) заменить d на max(d; 0), то алгоритм становится корректным.

Назовем алгоритм вычислительно устойчивым, если погрешность результата мала при малой погрешности округления (вычислительной погрешности).

Вычислительная неустойчивость алгоритма часто может быть выявлена благодаря анализу устойчивости по входным данным, т.к. неустойчивость к малым ошибкам округления входных данных автоматически свидетельствует о вычислительной неустойчивости алгоритма.

Пример 1.11. Пусть величина у_n для n = 1, 2,… вычисляется по рекуррентной формуле y_n = a_ny_n–1 + b_n, а значение у₀ задано. Тогда приближенные значения у*_n содержат ошибки, удовлетворяющие равенству y_n– y*_n= a_n(y_n–1 – y*_n–1). Следовательно, D(y*_n) = |a_n|×D(y*_n–1). Отсюда при | a_n | < 1 алгоритм устойчив по входным данным, поскольку D(y*_n) £ D(y*_n–1) для всех n. При | a_n | ³ q >1 алгоритм неустойчив, поскольку D(y*_n) ³ qⁿ ×D(y*₀) и погрешность неограниченно возрастает при n ® ¥.

Пример 1.12. Пусть требуется составить таблицу значений определенных интегралов для n = 1, 2,…. Интегрируя по частям, получим рекуррентную формулу

I_n = n I_n–1 – 1 (1.2)

при начальном условии I₀ = e – 1» 1.71828, которое легко находится непосредственно.

Результаты примера 1.10. предупреждают нас, что расчет по формулам (1.2) неустойчив, т.к. a_n = n >1. Действительно, при абсолютно точных вычислениях погрешность в 6-й значащей цифре начального условия приводит к тому, что I*₁₀ = – 6.536, в то время как все искомые значения интегралов, очевидно, положительны.

Попробуем изменить алгоритм, чтобы сделать его устойчивым. Перепишем (1.2) в виде

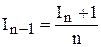(1.3)

и будем вести вычисления в обратном порядке, начиная, например с n = 54, положив I₅₄ = 0. Так как 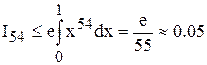, то D(I*₅₄) £ 0.05. При вычислении I₅₃ эта ошибка уменьшится в n раз, т.е. в 54 раза, при вычислении I₅₂ – еще в 53 раза и т.д. В результате интегралы при n = 50, … 1 будут вычислены с 7-ю верными значащими цифрами. То есть, при использовании формул (1.3), ошибки не растут, а затухают и модифицированный алгоритм устойчив.

Если говорить о связи и различии корректности вычислительных задач и вычислительных алгоритмов, то общий вывод таков. Если алгоритм, предназначенный для решения хорошо обусловленной задачи, оказался неустойчивым, то его следует признать неудовлетворительным и попытаться построить более качественный алгоритм. В примерах 1.10 и 1.12 это удалось сделать достаточно просто. Однако для плохо обусловленных задач дело обстоит иначе. Здесь требуется серьезное переосмысление постановки вычислительной задачи, поскольку решение плохо обусловленной задачи является объективно плохим и даже самый хороший алгоритм не улучшит его. Так, в примерах 1.7 и 1.8 все расчеты проводились абсолютно точно, тем не менее, результат отрицателен.

Дата добавления: 2014-01-11