Локализация корней

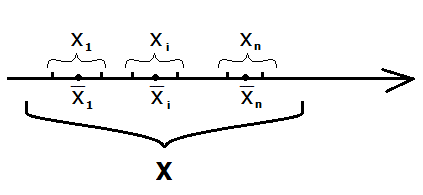
Для того, чтобы осуществить локализацию корней, необходимо найти достаточно малые интервалы 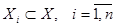, такие что:

1. 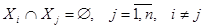– они не пересекаются между собой;

2. 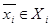– они содержат в себе корень исходного уравнения

Первый способ. Локализацию корней во многих случаях можно осуществить графически: достаточно построить график функции 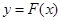, тогда действительные корни уравнения (1) – это точки пересечения 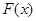с осью .

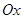Если график 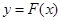построить затруднительно, то уравнение (1) следует попытаться представить в эквивалентном виде:

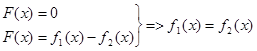(3)

с таким расчетом, чтобы графики функций строились проще. При этом корни уравнения (3) определяются как абсциссы точек пересечения графиков .

Задача 1.1.

Осуществить локализацию корней следующего уравнения:

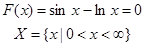
Решение. Введём две функции:

Далее необходимо визуально определить точки пересечения этих двух функций и записать интервалы, в которых они находятся. Точно вырисовывать графики на миллиметровой бумаге или с помощью компьютера вовсе не нужно. В данном случае достаточно понимания того, как ведут себя эти функции. Синус проходит через начало координат, далее при 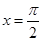равен единице, а далее снова равен нулю при 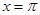. Логарифмическая функция равна нулю при и единице при .

Следующий график, конечно, построен на компьютере, но на самом деле хватит всего вышеупомянутых точек, чтобы увидеть интервал локализации:

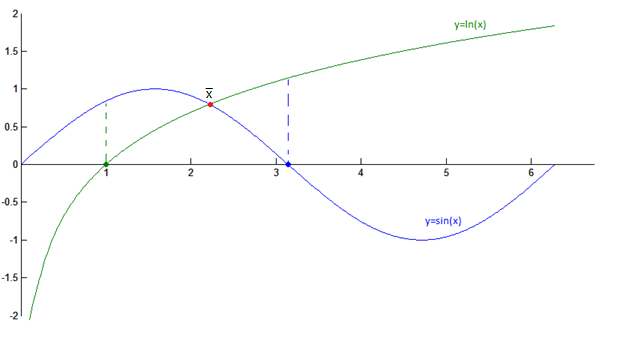
Ответ: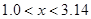

В более сложных (сомнительных) случаях локализацию корней для достоверности нужно подкрепить дополнительными вычислениями. При этом целесообразно использовать следующие достаточно очевидные положения:

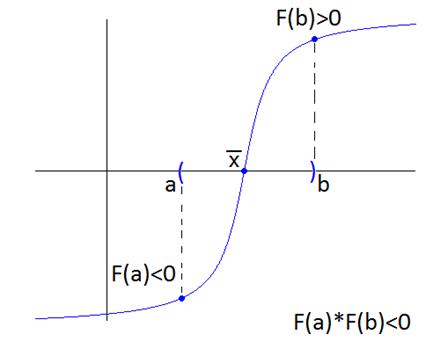
1. Если функция 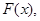которая непрерывна на отрезке 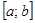, принимает на его концах значения разных знаков, то на интервале 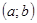уравнение имеет по меньшей мере один корень:

Замечание. Для корня чётной кратности это положение не выполняется, т.к. в малой окрестности такого корня 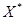функция 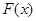имеет постоянный знак.

2. Второе положение – следствие из первого. Если 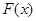строго монотонна отрезке 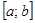, а также если 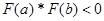(разные знаки на концах отрезка), то – единственный корень уравнения на данном отрезке.

Задача 1.2.

Локализовать корни уравнения .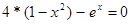

Решение. Вначале упростим себе жизнь и разделим обе части уравнения на 4, затем, как и в предыдущем примере, разделимся на 2 функции:

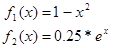
Построим графики. Опять же, несмотря на то, что ниже приведён график, нарисованный компьютерной программой, нам она вовсе не требуется. Достаточно только понять, что график параболы проходит через точки , и , а график экспоненты в точке принимает значение 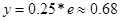, и левее этой точки асимптотически стремится к оси абсцисс. Начертив графики, проходящие через эти опорные точки, можно увидеть два наших корня:

Ответ:

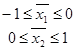
Осуществим проверку знакопеременности исходной функции 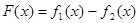на каждом из интервалов:

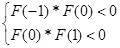
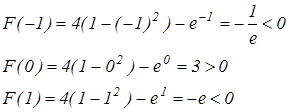
Значит на каждом из отрезков находится по крайней мере один корень.

В особо сложных случаях, когда функция слишком сложна для построения, используют построение таблицы значений функции 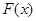на исследуемом интервале.

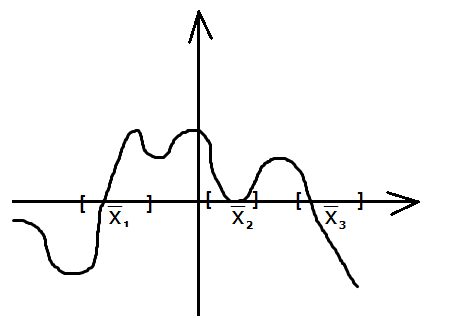
Задача 1.3.

Локализовать корни уравнения на интервале .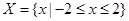

Решение. Локализуем корни данного уравнения первым способом.

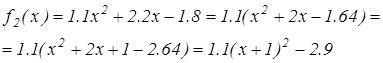
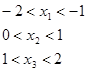
Но данный способ даёт грубые результаты. Второй способ более точный. Возьмём шаг 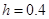и посчитаем значения функции от левой границы интервала до правой с этим шагом:

Видно, что функция меняет знак в трёх местах:

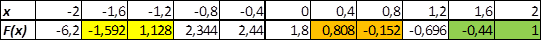
Значит корней всего три и мы их локализовали. Ответ:

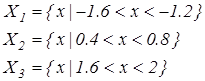
Дата добавления: 2014-01-15