Приклад 3.1

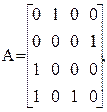
Як видно (див. мал. 3.2), через дві (k = 2) суміжні дуги можна потрапити: з вершини 1 у вершину 4, з 2 в 1, з 2 в 3, з 3 в 4, з 4 в 1 і з 4 в 2.

Таким чином, можна алгоритмічно визначити, чи існує шлях з v_i в v_j довжиною в k дуг. Очевидно, що якщо число вузлів m, максимальний ступінь k, у яку потрібно звести А для визначення самого довгого шляху, дорівнює (m - 1).

Матриця інцидентності – у загальному випадку прямокутна матриця В = {b_ij}, , , 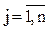де m – число вершин, n – число ребер. Для орграфов:

Для неорієнтованих:

Рис. 3.3

Таким чином, матриця структури зв'язків містить інформацію про взаємну орієнтацію пар дуг графа.

Крім цього, можуть використовуватися структурні матриці, що кодують окремі властивості графів:

- наявність контурів (контур = замкнутий шлях),

- наявність шляхів,

- відносини торкання.

Дотичними називаються шляхи, контури або шляхи з контурами, якщо вони містять хоча б один загальний вузол.

Сильнозв’язаним називається граф, у якому будь-який вузол досяжний з будь-якого іншого вузла.

Досяжність – це існування шляхи з вузла v_i у вузол v_j. Наприклад, на мал. 3.3 шлях з вузла 1 у вузол 4 має вигляд:

вузол 1 ® W₁ ® вузол 2 ® W₂ ® вузол 3 ® W₄ ® вузол 4.

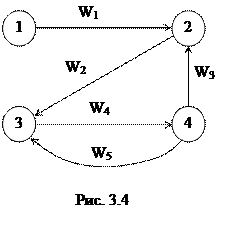
Може виявитися, що не всі вузли досяжні з інших вузлів. У цьому випадку може бути виділений підграф Г₁, тобто сукупність, підмножина вузлів, для якого умова сильної зв’язності виконується. Наприклад, граф Г (див. мал. 3.4) не сильнозв’язний, тому що у вузол 1 з вузлів 2, 3 і 4 немає шляхів. Сильнозв’язний компонент Г₁ для графа Г складається з вузлів 2, 3 і 4 з відповідними дугами W₂ – W₅.

Фізичний зміст сильної зв’язності - наявність зворотних зв'язків (ЗЗ) між всіма вузлами або, інакше кажучи, взаємозалежність (взаємовплив) всіх змінних у графі.

Важливість поняття «сильна зв’язність» випливає з того, що практично всі цілеспрямовані системи будуються на основі принципу зворотного зв'язку, коли інформація про вихідні величини (координати) деякого об'єкта використовується для формування керуючого сигналу U цим об'єктом.

Структура найпростішої системи керування описується графом (див. мал. 3.5), де W₁ можна інтерпретувати як модель об'єкта керування, а W₂ – модель керуючого пристрою. Вузли 1 - керування U, 2 і 4 можна інтерпретувати як вихідну величину об'єкта у; 3 (ε) - помилка регулювання, вузол 5 - завдання х (бажане значення величини у).

Рис. 3.5

4. Моделі систем

4.1. Цілі моделювання систем

Основними задачами моделювання є адекватне подання інформації для досягнення двох основних цілей: по-перше, для аналізу характеристик (властивостей) систем і, по-друге, для синтезу (розробки) систем, що відповідають заданим умовам. Маючи на увазі, що штучні системи є, в остаточному підсумку, системами керування, можна сказати, що метою моделювання при аналізі є оцінка характеристик систем при різних рівнях подання інформації про об'єкт, а при синтезі - розробка моделі керуючої частини системи (системи прийняття рішень).

Крім основних цілей, моделювання може використовуватися також для перевірки працездатності керуючого пристрою в різних режимах роботи (даний процес моделювання називається тестуванням), для поліпшення якості процесів керування (системи керування з моделлю), перевірки рішень паралельно з їхнім генеруванням (імітаційне моделювання) і т.д.

4.2. Рівні моделювання

4.2.1. Класифікація рівнів моделювання

Існує досить велика кількість класифікаційних ознак для моделей елементів і систем, однак, найбільш загальним є обсяг інформації, що несе в собі модель. Рівень визначеності інформації визначає границі, при яких модель і об'єкт або моделі різного виду зберігають гомоморфізм (іноді говорять «гоморфизм»), тобто можуть розглядатися як адекватні в змісті певних критеріїв близькості.

Із зазначеної точки зору виділимо наступні рівні моделювання:

1) Концептуальний рівень, коли визначаються границі системи (елемента), тобто вказуються вектори вхідних і вихідних координат системи (елемента).

2) Топологічний рівень, коли визначені зв'язки вхідних, вихідних і внутрішніх змінних систем. Моделями даного рівня є графи. Якщо, крім того, зазначені (хоча б у загальному виді, без завдання структури операторів) інтенсивності зв'язків, то моделями цього рівня є мережі.

3) Структурний рівень, коли визначена структура операторів, що описують взаємозв'язок вхідних, вихідних і внутрішніх змінних. Наприклад, взаємозв'язок може задаватися функціональними статичними співвідношеннями, операторами опису динаміки (диференціальні, інтегральні рівняння, передатні функції й т.д.), матричними перетвореннями й т.д.

4) Параметричний рівень, коли задані параметри операторів зв'язків, тобто модель даного рівня повністю визначена (у тім ступені, у якій визначені параметри) і над нею можуть проводиться найбільш інформативні експерименти й робитися розрахунки.

При використанні моделей різних рівнів виникають питання:

1) Які задачі дозволяє вирішувати модель того або іншого рівня?

2) Для яких задач модель кожного рівня є інформаційно не надлишкової?

Відповіді на ці питання дозволяють визначити мінімально припустимий рівень інформації для рішення тих або інших задач, що, у свою чергу, дозволяє мінімізувати витрати ресурсів на формування баз даних і розробку методів аналізу моделей.

4.2.2. Задачі аналізу властивостей систем, розв'язувані на концептуальному рівні

На концептуальному рівні можуть вирішуватися задачі декомпозиції (розбивки) на підсистеми й агрегації (об'єднання) підсистем у систему. Ці процедури є невід'ємними елементами аналізу й синтезу складних систем, у тому числі, на основі системного підходу. Основа методів декомпозиції й агрегації - думка експертів, фахівців предметної області.

4.2.3. Задачі, розв'язувані на топологічному рівні

На моделях топологічного рівня можуть вирішуватися наступні основні задачі:

1) визначення загальних характеристик і структурних властивостей системи,

2) визначення еквівалентних передач на графі (мережі),

3) виділення підсистем у системі.

Розглянемо шляхи рішення деяких задач.

I. Визначення структурних властивостей системи

Визначаються наступні характеристики:

Ступінь централізації, що оцінює тип структури, до якого тяжіє даний граф. Відомі кілька основних типів структур (див. мал. 4.1).

Рис. 4.1

Структури складних систем керування тяжіють до структур ієрархічного типу (див. мал. 4.2), ринкових господарських структур - до кістякового типу.

Рис. 4.2

Кількісно нерівномірність завантаження елементів графа характеризують індексами центральності. Для ненаправленого графа:

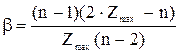, (4.1)

де

, (4.2)

n - число вершин графа,

d_ij – довжина мінімального шляху (при i = j довжина d_ij = 0).

Для графа на мал. 4.1, а, коли всі вершини інцидентні тій самій кількості ребер, b» 0. Для графа на мал. 4.1, в b» 1.

Для орієнтованого графа індекс центральності

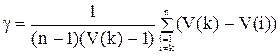, (4.3)

де V(i) = v_i + vⁱ – сумарне число вхідних і вихідних ребер i-й вершини, а .

Діаметр структури оцінюється максимальним числом зв'язків, що розділяють вхідні й вихідні елементи графа:

, (4.4)

де I – множина вершин-джерел, J – множина вершин-стоків, d_ij - мінімальний шлях від i до j.

Зв’язність – найменше число вершин, видалення яких приводить до незв'язного графа.

Реберна зв’язність – найменше число ребер, що приводить до незв'язного графа.

Відомі й інші характеристики: складність, наявність контурів, петель, сильноз в’язних компонент, відносини торкання й т.д.

II. Визначення еквівалентних передач

Потрібно встановити еквівалентний оператор, що описує зв'язок від i-го вузла до j-го вузла з урахуванням всіх зв'язків графа.

Для сигнальних графів Мезоном отримане наступне співвідношення:

, (4.5)

де? - визначник графа:

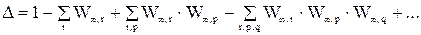(4.6)

W_¥,r (r = 1,2,…) - передатний коефіцієнт r-го розімкнутого контуру (визначається як добуток передач вхідних у контур дуг),

W_¥,r^. W_¥,p (p,r = 1, 2, …, r ¹ p) – добуток «пар» передатних коефіцієнтів недотичних контурів, далі аналогічно для «трійок», «четвірок» і т.д. недотичних контурів;

P_k – передача k-го прямого шляху, обумовлена як добуток передатних коефіцієнтів дуг, що утворять шлях;

Δ_k – мінор k-го прямого шляху (складається аналогічно визначнику, але для підграфа, отриманого з вихідного графа при видаленні вузлів, що належать k-му прямому шляху).

III. Виділення підсистем у системі

Задача може вирішуватися:

- формальними методами,

- концептуально (у цьому випадку концептуальне виділення повинне підтверджуватися на основі формальних процедур).

Формальні методи звичайно базуються на аналізі топології (структури системи), концептуальні - на функціональних характеристиках у тих або інших аспектах. Розглянемо формальні методи виділення підсистем, що базуються на двох основних підходах:

а) підсистемами вважаються незв'язні сильні компоненти графа. Порядок виділення наступний:

- визначається множина всіх сильнозв’язних компонентів;

- на отриманій множині виділяється підмножина пар, трійок і т.д. сильнозв’язних компонентів, які є недотичними.

б) підсистемами вважаються сильнозв’язні компоненти, що виходять при видаленні дуг-мостів. Аналіз графа звичайно проводиться в припущенні, що число дуг, що видаляються, повинно бути мінімально. Спочатку відшукуються одиничні дуги, видалення яких порушує сильну зв’язність графа, але зберігає не менш двох сильних компонентів. Якщо таких дуг нема, шукаються пари дуг, видалення яких викликає описаний ефект і т.д.

Концептуальні методи виділення підсистем базуються на неформальних ознаках виділення підсистем. Наприклад, для графа на мал. 4.3,а можна нарахувати п'ять сильнозв’язних компонент (крім самого графа), але концептуально підсистемами можна вважати, наприклад, підграфи, зображені на мал. 4.3, б и в.

Рис. 4.3

Перевірку сили зв’язності компонент можна здійснювати різними методами, зокрема:

- за допомогою матриці Брістоля [17 ],

- методу Розенброка (метод перевірки діагональної домінантності) [18 ],

- методу Вавилова-Імаєва [19 ].

Розглянемо останній метод докладніше на прикладі графа, зображеного на мал. 4.4. Припустимо, що системи S₁ і S₂ не зв'язані, тобто організовані в систему S помилково. Визначник такої незв'язної системи буде дорівнює

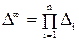, (4.7)

де n – число підсистем (у прикладі n = 2), Δ_i – визначник i-й підсистеми.

У прикладі

Δ₁ = 1 + W₁₁^.R₁₁, Δ₂ = 1 + W₂₂^.R₂₂, (4.8)

Δ_¥ = 1 + W₁₁^.R₁₁ + W₂₂^.R₂₂ + W₁₁^.R₁₁^.W₂₂^.R₂₂. (4.9)

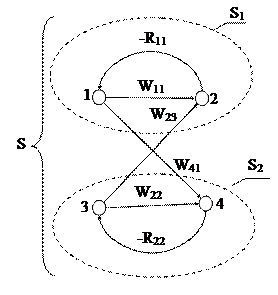Рис. 4.4

Визначник системи з урахуванням існуючих зв'язків:

Δ = 1 + W₁₁^.R₁₁ + W₂₂^.R₂₂ + W₁₁^.R₁₁^.W₂₂^.R₂₂ – W₂₃^.R₁₁^.W₄₁^.R₂₂. (4.10)

Можна бачити, що різниця визначників

δΔ = Δ - Δ_¥ = – W₂₃^.R₁₁^.W₄₁^.R₂₂. (4.11)

Очевидно, що якщо

, (4.12)

«добавкою» δΔ можна зневажити й підсистеми S₁ і S₂ розглядати як незалежні. Модуль в (4.12) береться тому, що, по-перше, «добавка» δΔ може бути як зі знаком «+», так і зі знаком «-», по-друге, значення δΔ, Δ і Δ_¥ - це не обов'язково дійсні числа. Оператори передач W_ij, K_kp (i, j, k, p – цілі числа) можуть бути довільними об'єктами, у тому числі комплексними числами й матрицями. Тому модуль може розумітися, принаймні, у трьох змістах:

- для дійсних чисел - число без знака (зі знаком «+»);

- для комплексних чисел p = α + j^.ω, де - мнима одиниця:

; (4.13)

- для матриць - визначник матриці.

4.2.4. Моделі структурного рівня

Розрізняють моделі елементів у статиці й у динаміку.

Моделями статики є функції виду

y = f(x),

де х и у відповідно вхідні й вихідні координати системи, які не залежать від часу або їхнього значення розглядаються як сталі (t®¥).

f - функція, що може задаватися аналітично, графічно або алгоритмічно.

Динамічні моделі й характеристики описуються лінійними й нелінійними диференціальними рівняннями, різницевими рівняннями. рівняннями в частинних похідних, операторними рівняннями, передатними функціями й ін.

4.2.5. Моделі параметричного рівня

Перш, ніж говорити про завдання параметрів, необхідно сказати, що параметри можуть бути обмірювані в різних шкалах. Існує чотири рівні вимірів:

1) шкала найменувань (приклади: Іванов, Еверест,…);

2) шкала порядку – є ознака, за якою виконується порівняння, але не обов'язково у вигляді числа (приклад: холодно – тепло – гаряче);

3) шкала інтервалів – використовуються числа, що характеризують різниці границь інтервалів (приклад: температура в гр. Цельсія або Фаренгейта);

4) шкала відносин.

Для шкал 3-го й 4-го рівнів справедливі групи аксіом:

1) аксіоми тотожності

А = В (або А ¹ В),

якщо А = В, то В = А,

якщо А = В и В = С, то А = С;

2) аксіоми рангового порядку (для їхнього виконання потрібно, щоб виконувалася умова порівнянності й транзитивності; наприклад, не можна порівнювати біфштекс із книгою)

якщо А > B, то B < A,

якщо А > В и В > С, то А > С (те ж для нестрогого порядку);

3) аксіоми адитивності

якщо А = Р и В > 0, то А + В > Р,

А + В = В + А,

якщо А = Р и В = Q, то А + В = P + Q,

(А + В) + С = А + (В + С).

Крім змінними, вимірюваними дійсними числами, існують комплексні числа, що задаються парою (а,в) дійсних чисел, одне з яких (а) умовно вимірює дійсну, а друге (в) - мниму складову.

Крім того, існують також змінні, вимірювані нечіткими, лінгвістичними «числами», які характеризуються парою (х, m_х), де х - нечітка змінна, m_х - функція приналежності до якої-небудь множини. За допомогою таких змінних вимірюють (оцінюють) людські відчуття. Дані числа складно віднести до якому-небудь із перерахованих вище типів і варто погодитися, що це особливий тип чисел.

4.3. Класифікація моделей систем

Одна з можливих класифікацій моделей, використовуваних у процесі аналізу й синтезу (створення) систем, представлена на мал. 4.5.

Серед моделей різного виду й призначення виділяються два принципово різних типи:

- перший тип призначений для опису характеристик (властивостей) систем, тобто для цілей аналізу;

- другий тип призначений для прийняття яких-небудь рішень із метою досягнення цілей.

Надалі ці типи моделей будемо умовно позначати як Мс – моделі систем і Мт – моделі вимог. Розглянуті вище приклади моделей, в основному, можуть бути віднесені до типу Мс.

Рис. 4.5

Основними елементами моделей типу Мт є:

- цілі й критерії, за якими здійснюється вибір рішення;

- моделі прийняття рішень: закони регулювання й керування, алгоритми формування керувань, схеми й процедури прийняття рішень і т.д.

Всі можливі варіанти постановки задач побудови цілеспрямованих систем є бінарними відносинами (декартовим добутком) цих двох типів моделей

S = Мс ´ Мт.

Далі в п.п. 4.4 і 4.5 будуть розглянуті деякі види моделей типів Мс і Мт.

4.4. Моделі систем типу Мс

Розглянемо кілька видів класифікаційних ознак і відповідні класи моделей, не претендуючи на спробу обґрунтування їхнього вибору. Зазначимо тільки, що поєднання різних класифікаційних ознак можуть утворювати досить велику розмаїтість практично виділюваних класів моделей.

Апроксиматори, називані також у літературі «чорними ящиками» (black box), «формальними моделями», є різновидом математичних моделей, описують функціональні зв'язки між входами й виходами моделюємої системи без обліку (при відсутності) яких-небудь знань про топологію системи. Коефіцієнти таких моделей можуть не мати якого-небудь фізичного змісту, не співвідносяться, наприклад, з технологічними параметрами процесів. У цьому полягає недолік таких моделей. Однак, ці моделі ефективні у випадку неможливості або труднощі побудови строгих математичних описів поводження систем.

Розповсюдженими прикладами таких моделей є нейронні мережі (НС).

Механістичні моделі. Якщо знання про функціонування моделі формалізовані, то для опису таких моделей можуть бути використані механістичні моделі (ММ), до числа яких відносять:

- алгебраїчні моделі (АМ), що представляють собою системи алгебраїчних і трансцендентних рівнянь,

- диференціальні рівняння (ДР) і системи ДР,

- передатні функції (ПФ),

- логічні моделі (ЛМ) і ін.

Такі моделі звичайно одержують шляхом аналізу фізичних і хімічних основ моделюємих процесів. Результатом аналізу є пряма або зворотна модель процесу. Пряма модель відбиває вплив вхідних координат процесу на вихідні й може бути представлена у вигляді функції

Y = F(X),

де Х и Y - множини вхідних (у тому числі керуючих) і вихідних координат відповідно.

У ряді випадків необхідним є одержання зворотної моделі виду

X = Q(Y_н),

де Y_н - множина спостережуваних або вимірюваних значень вихідних координат процесу. У більшості випадків побудова зворотних моделей є некоректною задачею, тобто має більше одного рішення або взагалі його не має.

Статистичні моделі є технологією побудови моделей шляхом опису властивостей процесу через статистичні змінні й відповідні статистичні оцінки цих змінних. По своїй суті ці моделі містять елемент невизначеності.

Моделі, відповідно до цієї технології, будуються з використанням методів статистичного аналізу, теорії ігор, теорії інформації й т.п.

Різновидами даних моделей є імовірнісні й кореляційні моделі. Імовірнісні моделі використовують щільності ймовірності змінних процесу. При цьому найбільше часто використовуються нормальний і експонентний закони розподілу. Використання таких моделей обмежене тим, що при числі змінних більше двох потрібне велике число експериментів, виникають труднощі, пов'язані з кореляцією параметрів.

Динамічні моделі й характеристики описують поводження систем у динаміці, тобто в часі.

Найбільше часто динамічні моделі представляються лінійними й нелінійними диференціальними рівняннями, різницевими рівняннями в частинних похідних, операторними рівняннями, передатними функціями й ін.

Лінійними називаються елементи, для яких справедливий принцип суперпозиції:

L(х₁ + х₂) = L(х₁) + L(х₂),

де L - деякий оператор.

Такою властивістю володіють оператори підсумовування, інтегрування, диференціювання.

При дослідженні динамічних властивостей систем може бути використані прикладні математичні методи операційного вирахування. Наприклад, функціонування деякої системи описується ДР виду

, (4.14)

де х и в - вхідна й вихідна величини. Якщо в дане рівняння замість x(t) і y(t) підставити функції X(s) і Y(s) комплексного змінного s такі, що

і 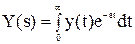, (4.15)

тоді ДР (4.14) при нульових початкових умовах рівносильне лінійному алгебраїчному рівнянню

a₂ s² Y(s) + a₁ s Y(s) + a₀ Y(s) = b₁ X(s) + b₀ X(s).

Такий перехід від ДР до алгебраїчного рівняння називається перетворенням Лапласа, формули (2.2) відповідно формулами перетворення Лапласа, а отримане рівняння - операторним рівнянням.

Нові функції X(s) і Y(s) називаються зображеннями для x(t) і y(t) по Лапласові, тоді як x(t) і y(t) є оригіналами стосовно X(s) і Y(s).

Перехід від однієї моделі до іншої полягає в заміні знаків диференціалів на оператори sⁿ, знаків інтегралів на множники 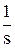, а самих x(t) і y(t) - зображеннями X(s) і Y(s).

Для зворотного переходу від операторного рівняння до функцій від часу використовується метод зворотного перетворення Лапласа. Загальна формула зворотного перетворення Лапласа:

,

де f(t) - оригінал, F(jw) - зображення при s = jw, j - мнима одиниця, w - частота.

Перетворення ДР по Лапласові дає можливість увести поняття передатної функції, що характеризує динамічні властивості системи.

Наприклад, операторне рівняння

3s²Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)

можна перетворити, винісши X(s) і Y(s) за дужки й поділивши один на одного:

Y(s)*(3s² + 4s + 1) = X(s)*(2s + 4),

.

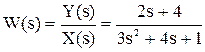Отримане вираження називається передатною функцією.

Передатна функція - це відношення зображення вихідного впливу Y(s) до зображення вхідного X(s) при нульових початкових умовах:

.

Передатна функція для лінійних елементів часто є дрібно-раціональною функцією комплексної змінної:

,

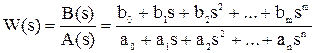де B(s) = b₀ + b₁s + b₂ s² + … + b_m s^m - поліном чисельника,

А(s) = a₀ + a₁s + a₂ s² + … + a_n sⁿ - поліном знаменника.

Якщо замість s підставити вираження s = jw, одержуємо перетворення Фур'є, що характеризує зв'язок між частотними характеристиками вхідних і вихідних сигналів елемента. Частотні характеристики дають можливість аналізувати опис системи з урахуванням динаміки.

Останнім часом більш широко використовується опис динаміки систем методом простору станів.

Для опису динаміки елементів систем використовується в даному методі матричний запис ДР:

, (4.16)

де А - матриця коефіцієнтів, U - матриця входів або керувань, Х - матриця простору станів:

Х = (х₁, х₂, … х_n)^Т.

У цьому випадку х_i називається змінної стану або фазовий змінної («Т» – символ транспонування).

Припустимо, що динамічні властивості об'єкта описуються ДУ виду

, (4.17)

де a_i і b_i – коефіцієнти, у – вихідний сигнал, u – вхідний сигнал об'єкта.

Якщо ввести змінні стани:

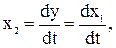
і т.д.,

те ліва частина ДР (4.17) прийме вид (після ділення на (-а_n ):

.

Можна записати рівняння в матричному виді:

.

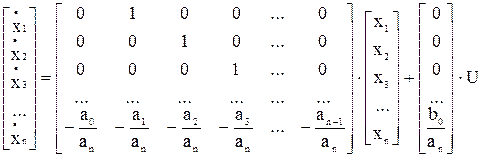Рішенням отриманого матричного рівняння є матриця Х.

Для визначення вихідних параметрів y_i рівняння (4.16) доповнюється рівнянням

Y = C^.X + D^.U,

де С (p´n) – матриця зв'язків, D (p´q) – матриця обходу, p – число вихідних параметрів у_i, q – число вхідних параметрів u_i.

Рішення матричних рівнянь для деяких випадків може бути зроблене аналітично, зокрема, для однорідного ДР виду

. (4.18)

Пряме перетворення Лапласа для даного рівняння дає

s^.X(s) – X₀ = A^.X(s),

де Х₀ – матриця початкових умов, тобто початкові умови по змінній у, по швидкості її зміни, прискоренню й т.д. Звідси отримане

Х(s) = X₀^.[s^.E – A]^-1 = Ф(s)^.X_0,

де Е - одинична матриця, Ф(s) - зображення фундаментальної матриці

Ф(s) = [s^.E – A]^-1.

Оригіналом фундаментальної матриці є матричний експоненціал

.

Тоді рішення ДР (4.18) можна одержати у вигляді ряду із кроком Dt за часом:

Х₀ – початкові умови,

Х(Dt) = Ф(Dt)^.Х₀,

Х(2^. Dt) = Ф(2^.Dt)^.Х(Dt) і т.д.

Дата добавления: 2014-01-11