
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над графами
а) Дополнением графа G(V,E) называется граф 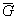 (V,E), такой, что для любых u,v
(V,E), такой, что для любых u,v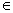 V, ребро {u,v} графа
V, ребро {u,v} графа 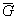 существует тогда и только тогда, когда это ребро в G отсутствует.
существует тогда и только тогда, когда это ребро в G отсутствует.
б) Пусть даны два графа G1(V1,E1) и G2(V2,E2).
1) Объединением графов G1 и G2 (обозначается G1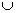 G2) называется граф G = G1
G2) называется граф G = G1 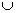 G2=(V1
G2=(V1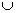 V2, E1
V2, E1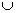 E2).
E2).
2) Пересечением графов G1 и G2 (обозначается G1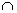 G2) называется граф G = G1
G2) называется граф G = G1 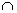 G2=(V1
G2=(V1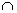 V2, E1
V2, E1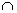 E2).
E2).
3) Соединением графов G1 и G2 (обозначается G1+ G2) называется граф
G1+ G2 =(V1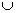 V2, E1
V2, E1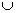 E2
E2 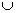 {{u,v}
{{u,v}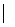 u
u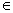 V1, v
V1, v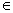 V2, u ≠v}).
V2, u ≠v}).
Кроме этих операций, для графов определяются также и другие операции: кольцевая сумма, прямое произведение, удаление и добавление вершин и рёбер, стягивания дуги и т.д.
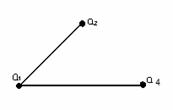
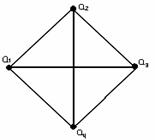
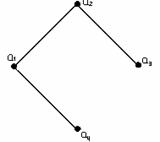
Пример 3.2.2 - На рисунке 3.2.5 изображены графы, представляющие результаты операций над графами G1 и G2 .
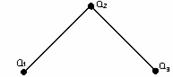
| 
| ||||
| |||||
G1+ G2 G1 G2 G1
G2 G1 G2
G2
Рисунок 3.2.5
Рассмотрим ещё два важных вида графов:
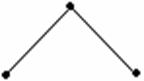
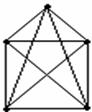 а) полный граф с n вершинами обозначается Кn (н-граф без петель и кратных рёбер называется полным, если любые его две вершины соединены ребром). На рисунке 3.2.6 изображены полные графы.
а) полный граф с n вершинами обозначается Кn (н-граф без петель и кратных рёбер называется полным, если любые его две вершины соединены ребром). На рисунке 3.2.6 изображены полные графы.
| 
| ||||
| |||||
К2 К3 К4 К5
Рисунок 3.2.6
Число рёбер полного графа вычисляется по формуле: m(Kn)=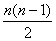 ;
;
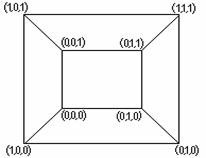
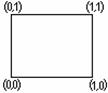
б) n –мерные кубы (n-кубы), обозначаются Qn. Вершинами Qn являются всевозможные n-ки, состоящие из 0 и 1. Так как всего таких наборов 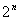 , то вершин у Qn будет
, то вершин у Qn будет 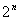 . Рёбра задаются по следующему правилу: вершины смежны тогда и только тогда, когда соответствующие n-ки отличаются ровно одной координатой. На рисунке 3.15 изображены кубы
. Рёбра задаются по следующему правилу: вершины смежны тогда и только тогда, когда соответствующие n-ки отличаются ровно одной координатой. На рисунке 3.15 изображены кубы 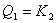 , Q2 и Q3.
, Q2 и Q3.
| |||||
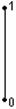
| |||||
| |||||
Рисунок 3.2.7
Пример 3.2.3 - Рассмотрим различные графы, иллюстрирующие выше приведённые определения и понятия (рисунок 3.2.8):
| |||||||
| |||||||
| 
| ||||||
| |||
| |||
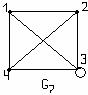
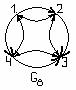
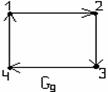
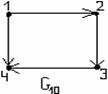
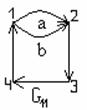
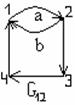
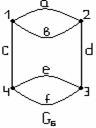
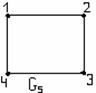
Рисунок 3.2.8
а) G1- G7 - н-графы, G8- G12 - орграфы;
б) G1 и G2 полные графы, причём G1= G2;
в) G7 – не является полным, т.к. имеет одну петлю;
г) G3 нуль-граф,т.к. все его вершины изолированные;
д) G4 и G5 являются дополнением друг к другу: G4= 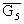 и G5=
и G5=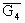 ;
;
е) G6 – мультиграф, т.к. содержит кратные рёбра a и b, e и f;
ж) G8 – орграф, канонически соответствующий н-графу G5;
и) G9 и G10 не являются равными, т.к. имеют отличающиеся дуги: в G9 - (4,1), в G10 - (1,4);
к) G11 – ориентированный мультиграф, дуги а и b кратные;
л) G12 – не является мультиграфом, т.к. дуги а и b различно
ориентированы.
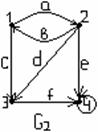
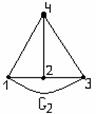
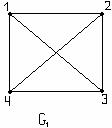
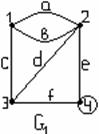 Пример 3.2.4 - Найти степени вершин графов G1 и G2 , изображённых на рисунке 3.2.9.
Пример 3.2.4 - Найти степени вершин графов G1 и G2 , изображённых на рисунке 3.2.9.
Рисунок 3.2.9
Решение: оба графа имеют по четыре вершины, т.е. V={1,2,3,4} – множество вершин и G1 и G2.
а) степени вершин н-графа G1. ρ(1)=3, ρ(2)=4, ρ(3)=3, ρ(4)=4.
Итак, 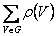 =14 =2m, m=7– число рёбер;
=14 =2m, m=7– число рёбер;
б) степени вершин орграфа G2 . Степени выхода: ρ1(1)=2, ρ1(2)=3, ρ1(3)=1, ρ1(4)=1. Степени входа: ρ2(1)=1, ρ2(2)=1, ρ2 (3)=2, ρ2(4)=3. Таким образом, 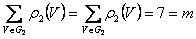 .
.
3.3 Лекция 11. Маршруты. Связность
Содержание лекции: маршруты, цепи, пути, циклы, контуры; связность, компоненты связности; определение компонент связности; исследование маршрутов.
Цели лекции: ввести новые понятия; определять компоненты связности; с помощью матрицы смежности определять длину и количество маршрутов.
Маршруты, достижимость, связность
Введём ещё несколько новых понятий для н-графа и орграфа одновременно.ПустьG(V,E) граф. Последовательность v1,e1, v2,e2, ….., en,vn+1, где v 1,v2,...,vn+1 V, e1,e2, …,en
V, e1,e2, …,en E, называется маршрутом, соединяющим вершины v1 и vn+1. Маршрут можно задать также последовательностью его вершин v1, v2, ...vn+1 или последовательностью его рёбер e1, e2, ...,en . Вершина v1- начало маршрута, vn+1 – конец.
E, называется маршрутом, соединяющим вершины v1 и vn+1. Маршрут можно задать также последовательностью его вершин v1, v2, ...vn+1 или последовательностью его рёбер e1, e2, ...,en . Вершина v1- начало маршрута, vn+1 – конец.
Цепь (путь) – маршрут, в котором все рёбра (дуги) различны.
Цикл (контур) – замкнутая цепь (контур), т.е. v1=vn+1.
Простая цепь (путь), простой цикл (контур) - цепь (путь), цикл (контур) не пересекающие себя, т.е. не содержащие повторяющихся вершин, кроме, может быть, первой и последней.
Граф, не содержащий циклов (контуров), называется ациклическим (безконтурным).
Число рёбер (дуг) маршрута называется его длиной. Если существует цепь (путь) длины n, соединяющая вершины u и v, то будем писать u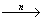 v.
v.
Вершина v достижима из вершины u, если существует цепь (путь) с началом в u и концом в v.
Определение.Н-граф называется связным, если любые его две несовпадающие вершины соединены маршрутом; орграф называется связным, если соответствующий ему н-граф является связным; орграф называется сильно связным, если любые его две вершины u и v взаимно достижимы, т.е. u достижима из v и v достижима из u.
Определение. Подграф G1 графа G называется компонентой связности (сильной компонентой связности) графа G (или связной (сильно связной) компонентой), если: 1) G1 – непустой связный (сильно связный) граф; 2) если G2 – связный (сильно связный) подграф графа G и G1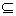 G2 , то G1 = G2 , т.е. G1 – максимальный связный (сильно связный) подграф графа G.
G2 , то G1 = G2 , т.е. G1 – максимальный связный (сильно связный) подграф графа G.
Пример 3.3.1 - Для н-графа G на рисунке 3.3.1 можно определить следующие понятия:
а) (v1,v3,v4) – простая цепь;
б) (v1,v3,v2,v1,v3,v4) – маршрут;
в) (v3,v1,v2, v4) не маршрут (т.к. нет ребра {v2,v4 });
г) (v1,v2,v3,v1) – простой цикл;
д) вершины v1,v2,v3,v4 - попарно достижимы; v5,v6 – цепь длиной 1, v7 – изолированная вершина или цепь длиной 0;
е) граф G не является связным, он имеет три компоненты связности с множеством вершин {v1,v2,v3,v1}, {v5,v6}, {v7}.
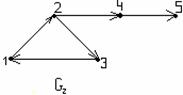
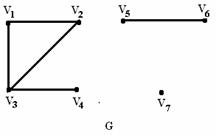
Рисунок 3.3.1 Рисунок 3.3.2
Пример 3.3.2 - Для орграфа G2 на рисунке 3.3.2 имеет место:
а) 1, 2, 4, 5 или 1, 2, 3 – простой путь;
б) 1, 2, 3, 1 – простой контур;
в)вершина 5 достижима из любой вершины, из вершины 5 не достижима ни одна вершина; вершина 4 достижима из 1, 2, 3 и не достижима из 5;
г) этот граф связный, но не сильно связный. Он имеет три сильные компоненты связности, задаваемые множеством вершин {1,2,3}, {4}, {5}.
Теорема. Любой граф может быть представлен в виде объединения непересекающихся связных (сильно связных) компонент. Разложение графа на связные (сильно связные) компоненты однозначно.
Таким образом, множество вершин связных (сильно связных) компонент образуют разбиение множества вершин графа.
Число связных (сильно связных) компонент графа G (обозначается K(G) или C(G)) определяется однозначно. Если K(G)=1, то граф G связный, если K(G)>1, то G - несвязный граф.
Для орграфа G2 из примера 3.3.2 число сильно связных компонент K(G2)=3, а множество вершин {1,2,3,4,5} имеет разбиение {{1,2,3},{4},{5}}.
Определение компонент связности и сильных компонент связности
Рассмотрим ещё одну матричную характеристику графа.
Определение.Квадратная матрица С=(сij) порядка n (n - число вершин) называется матрицей достижимости (для н-графа матрицей связности), если
сij = 
Матрицу достижимости можно получить следующим образом: пусть А – матрица смежности, составим матрицу B=(bij)=Е+А+А2+...+Аn , тогда
сij = 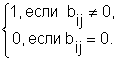
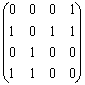
Заметим, что существуют другие способы определения матрицы достижимости. В простых случаях матрицу С можно составить по рисунку графа, например, для графа G2 из примера 3.3.2 матрица достижимости будет иметь вид: С=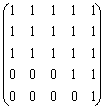 . Если все элементы матрицы достижимости
. Если все элементы матрицы достижимости
н-графа сij=1, то граф связный. В общем случае матрица C н-графа является матрицей отношения эквивалентности, соответствующей разбиению множества вершин графа на компоненты. Например, для графа G из примера 3.3.1 матрица связности будет: С= . Блоки, состоящие из единиц, соответствуют трём компонентам связности с множеством вершин {1,2,3,4}, {5,6}, {7}, т.е. разбиению множества вершин графа на эти компоненты.
. Блоки, состоящие из единиц, соответствуют трём компонентам связности с множеством вершин {1,2,3,4}, {5,6}, {7}, т.е. разбиению множества вершин графа на эти компоненты.
Для орграфа с помощью матрицы достижимости можно найти сильные компоненты связности.
Рассмотрим, кроме матрицы С=(cij), ещё две матрицы Q и S. Q=CT=(qij), где qij = Иногда матрицу Q называют матрицей контрдостижимости. S = (sij) = C
Иногда матрицу Q называют матрицей контрдостижимости. S = (sij) = C  Q где операция
Q где операция  означает поэлементное произведение матриц C и Q, т.е. sij=cij
означает поэлементное произведение матриц C и Q, т.е. sij=cij qij.
qij.
Так как вершины vi и vj находятся в одной сильно связной компоненте, если они взаимно достижимы, то, очевидно, что соответствующий элемент матрицы S равен 1: sij=1. Итак, сильно связная компонента, содержащая вершину vi, состоит из вершин vj, для которых sij=1.
Пример 3.3.3 - Рассмотрим орграф G2 из примера 3.3.2. Его матрица
достижимости С была найдена: С = 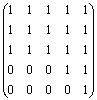 . Q = CT =
. Q = CT = 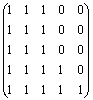 -
-
матрица контрдостижимости. Матрица S = C Q =
Q =
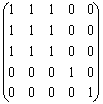 .
.
В первой строке матрицы S три единицы, которые соответствуют вершинам 1, 2, 3, это значит, что сильная компонента, содержащая вершину 1, содержит также вершины 2 и 3, т.е. является множеством {1,2,3}. Мысленно вычёркиваем из матрицы S строки и столбцы, соответствующие вершинам 1, 2, 3, в оставшейся матрице S1=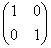 в первой строке одна единица, отвечающая вершине 4, следовательно, вторая сильная компонента есть множество {4}. Вычёркиваем из S1 строку и столбец, соответствующие вершине 4, в оставшейся матрице S2= (1) всего одна единица, которая соответствует вершине 5, т.е. последняя компонента сильной связности будет {5}. Итак, граф имеет три компоненты сильной связности {1,2,3}, {4}, {5}.
в первой строке одна единица, отвечающая вершине 4, следовательно, вторая сильная компонента есть множество {4}. Вычёркиваем из S1 строку и столбец, соответствующие вершине 4, в оставшейся матрице S2= (1) всего одна единица, которая соответствует вершине 5, т.е. последняя компонента сильной связности будет {5}. Итак, граф имеет три компоненты сильной связности {1,2,3}, {4}, {5}.
Исследование маршрутов графа
Важным применением матрицы смежности является возможность по ней определять маршруты фиксированной длины и их количество.
Теорема. Пусть дан граф G=(V,E), где V={v1,v2,…,vn} – множество вершин, A – матрица смежности графа G. Рассмотрим матрицу Ak= A A
A …
…
 A=(aij). Если aij=m, то из вершины vi в вершину vj существует m маршрутов длины k.
A=(aij). Если aij=m, то из вершины vi в вершину vj существует m маршрутов длины k.
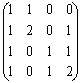
Пример 3.3.4 - Рассмотрим граф смешанного типа.
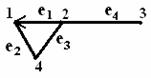
Рисунок 3.3.3
Его матрица смежности будет матрица А=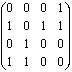 . По матрице А устанавливаем существование маршрутов длины 1, например, т.к. а13 =0, то
. По матрице А устанавливаем существование маршрутов длины 1, например, т.к. а13 =0, то
маршрутов из 1 в 3 длины 1 нет (записывают: маршрута (1 3) нет).
3) нет).
А2 = 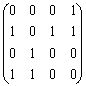

 =
=  . Т.к. а213 = 0, то маршрута (1
. Т.к. а213 = 0, то маршрута (1 3) нет, т.к. а222 =2, то существует два маршрута (2
3) нет, т.к. а222 =2, то существует два маршрута (2 2), т.к. а234 =1, то существует один маршрут (3
2), т.к. а234 =1, то существует один маршрут (3 4) и т.д.
4) и т.д.
А3 = 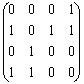

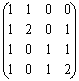 =
=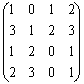 . Т.к. а313 =1, то существует один маршрут (1
. Т.к. а313 =1, то существует один маршрут (1 3), т.к. а321 =3, то существует три маршрута (2
3), т.к. а321 =3, то существует три маршрута (2 1) и т.д.
1) и т.д.
Последовательность вершин маршрута можно получить, исследуя элементы матриц А, А2, А3 и т.д., или, в случае простых графов, по их
рисунку. Наиболее наглядный способ состоит в использовании модифицированной матрицы смежности, в которой вместо единиц записаны названия соответствующих рёбер (дуг). В примере 3.3.4 модифицированная матрица смежности будет иметь вид:  .
.
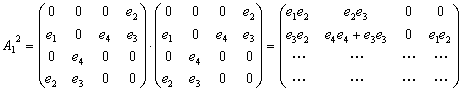 . По последней матрице делаем вывод, что т.к. её элемент
. По последней матрице делаем вывод, что т.к. её элемент 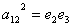 , то есть один маршрут длины 2 из вершины 1 в вершину 2, это
, то есть один маршрут длины 2 из вершины 1 в вершину 2, это 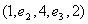 ; т.к.
; т.к.  , то есть два маршрута длины 2 из вершины 2 в 2:
, то есть два маршрута длины 2 из вершины 2 в 2: 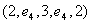 и
и 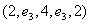 . По
. По  аналогично можно найти маршруты длины 3 и их количество.
аналогично можно найти маршруты длины 3 и их количество.
3.4 Лекция 12. Расстояния в графах. Задача о кратчайшем пути
Содержание лекции: расстояния в графах; взвешенные графы; задача нахождения кратчайших путей.
Цели лекции: рассмотреть некоторые приложения графов на практике: а именно, определение кратчайших маршрутов.
Расстояния в графах, взвешенные графы
Пусть G=(V,E) связный н-граф, vi, vj – две не совпадающие вершины G.
Определение. Расстоянием между вершинами vi и vj (обозначается
d(vi, vj)) называется минимальная длина простой цепи с концами в vi и vj.
Пусть V={v1,v2,…,vn} – множество вершин графа. Рассмотрим матрицу D=(dij), где dij =d(vi, vj). D называется матрицей расстояний. Очевидно, D=DT , т.е. D – симметрическая матрица.
Введём ещё несколько понятий:
1. Эксцентриситетом вершины v (обозначается e(v)) называется max{d(u,v)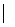 u
u v}, т.о. эксцентриситет равен расстоянию от данной вершины до наиболее удалённой от неё. В матрице расстояний e(vi) равен наибольшему из чисел, стоящих в і-ой строке.
v}, т.о. эксцентриситет равен расстоянию от данной вершины до наиболее удалённой от неё. В матрице расстояний e(vi) равен наибольшему из чисел, стоящих в і-ой строке.
2. Диаметром графа G (обозначается d(G)) называется максимальный из всех эксцентриситетов: d(G)=max{e(v)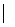 v
v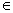 V}.
V}.
4. Радиусом графа G (обозначается r(G)) называется минимальный из всех эксцентриситетов: r(G)=min{e(v)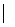 v
v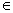 V}.
V}.
5. Вершина v называется периферийной, если e(v)=d(G); вершина v называется центральной, если e(v)=r(G). Множество всех центральных вершин графа называется его центром.
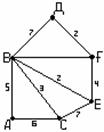
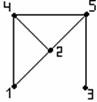 Пример 3.4.1 - Рассмотрим граф на рисунке 3.4.1.
Пример 3.4.1 - Рассмотрим граф на рисунке 3.4.1.
D=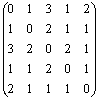 - матрица расстояний графа.
- матрица расстояний графа.
Рисунок 3.4.1
Наибольшее число в строке - это эксцентриситет соответствующей вершины, поэтому e(1) =3, e(2) =2, e(3) =3, e(4) =2, e(5) =2. Диаметр графа d(G)=3, как наибольший из эксцентриситетов, радиус - r(G)= 2, как наименьший. Вершины 1, 3 – периферийные, вершины 2,4,5 – центральные, множество {2,4,5} – центр графа.
Задача нахождения центральных вершин часто возникает на практике, например, если вершинам графа соответствуют районы города, рёбрам – дороги между ними. Требуется оптимально разместить учреждения общего пользования (больницы, рынки, и т.д.). Очевидно, что в этом случае оптимизация заключается в минимизации расстояний от самых отдалённых районов до этих учреждений. Следовательно, местами размещения должны быть центральные вершины графа. Реальные задачи от этих идеальных отличаются тем, что приходится учитывать и другие обстоятельства: расстояние между районами, стоимость проезда, время проезда и т.д. Для учёта различных обстоятельств используют взвешенные графы.
Определение.Пусть дан граф G(V,E). Пометкой (или распределением меток) графа называется пара функций: f: V Sv и g: E
Sv и g: E SE, где Sv, SE – множества меток вершин и рёбер (дуг). Четвёрка (V,E,f,g) называется взвешенным или помеченнымграфом.
SE, где Sv, SE – множества меток вершин и рёбер (дуг). Четвёрка (V,E,f,g) называется взвешенным или помеченнымграфом.
Если v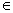 V, то f(v) – вес вершины v; если e
V, то f(v) – вес вершины v; если e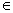 E, то g(e) – вес дуги e. Часто бывают помеченными только вершины или только рёбра (дуги).
E, то g(e) – вес дуги e. Часто бывают помеченными только вершины или только рёбра (дуги).
Пример 3.4.2 -На рисунке 3.4.2 изображён помеченный граф (V,E,f,g), представляющий схему автомобильных дорог с указанием их длины.
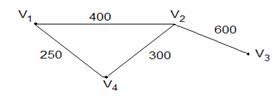
Рисунок 3.4.2
V1 - Астана, V2 - Экибастуз, V3 - Семипалатинск, V4 - Караганда.
V={V1, V2, V3, V4}, Е={{V1, V2 },{V2, V3}, { V1, V4},{ V2, V4}}, f: V Sv: Sv – множество городов, f(V1)= Астана, f(V2)= Экибастуз, f(V3)= Семипалатинск, f(V4)= Караганда. g: E
Sv: Sv – множество городов, f(V1)= Астана, f(V2)= Экибастуз, f(V3)= Семипалатинск, f(V4)= Караганда. g: E SE : SE – множество расстояний, g({V1, V2})=400, g({V2, V3})=600, g({V1, V4})=250, g({V2, V4})=300.
SE : SE – множество расстояний, g({V1, V2})=400, g({V2, V3})=600, g({V1, V4})=250, g({V2, V4})=300.
Информацию о весах дуг во взвешенном графе можно представлять в виде матрицы весов W=(wij), где wij – вес дуги (vi,vj), если эта дуга существует, если не существует, то соответствующий вес обозначают 0 или ∞, в зависимости от приложений (∞ - если вершины не смежные). Для графа из примера 3.4.2 матрица весов имеет вид: W= .
.
Для взвешенных графов аналогично вводятся понятия расстояния, эксцентриситета и т.д.
Нахождение кратчайших маршрутов (путей)
Существуют различные способы (алгоритмы) определения кратчайших маршрутов. Выбор каждого из них зависит от условий задачи (например, весы рёбер отрицательные или нет), от способа решения (вручную или на компьютере) и т.д.
Рассмотрим алгоритм Дейкстры, который можно использовать только для взвешенных графов с неотрицательными весами всех рёбер. Рассмотрим два варианта алгоритма Дейкстры (с использованием и нет матрицы весов).
Алгоритм Дейкстры 1.
Пусть G(V,E) – взвешенный граф, имеющий n вершин и W=(wij), его матрица весов 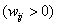 . Пусть требуется найти взвешенное расстояние от фиксированной вершины vі (она называется источником) до некоторой другой вершины (вообще по алгоритму Дейкстры 1 находят сразу расстояния от источника до всех остальных вершин).
. Пусть требуется найти взвешенное расстояние от фиксированной вершины vі (она называется источником) до некоторой другой вершины (вообще по алгоритму Дейкстры 1 находят сразу расстояния от источника до всех остальных вершин).
Обозначим Т1 множество вершин V - { vi}, т.е. Т1 – это множество всех вершин V без источника. Обозначим D(1)=(d1(1), d2(1), …, dn(1)), где di(1)=0,
dj(1)= wij (i≠j), т.е. D(1) – это і-ая строка в матрице весов.
Пусть на шаге S уже определены множества вершин TS и строка D(S)=(d1(S), d2(S), …, dn(S)). Наша задача перейти от TS к TS+1 и от D(S) к D(S+1).
Выберем в TS вершину vj такую, что dj(S)=min{ dk(S)/ vk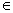 TS}. Положим ТS+1=TS{
TS}. Положим ТS+1=TS{ 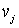 }, D(S+1)=(d1(S+1), …, dn(S+1)),
}, D(S+1)=(d1(S+1), …, dn(S+1)), 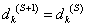 , если
, если 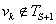 ,
,
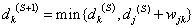 , если
, если 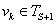 .
.
На шаге S = n-1 получим строку D(n-1)=(d1(n-1), d2(n-1)…, dn(n-1)), в которой dj(n-1) равно взвешенному расстоянию от вершины vі до вершины vj: d j(n-1)=dw(vі, vj).
 Пример 3.4.3 - Рассмотрим граф на рисунке 3.4.3.
Пример 3.4.3 - Рассмотрим граф на рисунке 3.4.3.
W=  - матрица весов.
- матрица весов.
Рисунок 3.4.3
Пусть требуется найти кратчайшие взвешенные расстояния от вершины A (источник) до остальных вершин. V={A,B,C,D,E,F} – множество вершин.
Будем полагать, что min(a,∞)=a, min(∞,∞)=∞, a+∞=∞, ∞+∞=∞.
1 шаг. А- источник,  ,
, 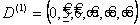 .
.
2 шаг. В  выбираем среди элементов, отмеченных ^ (т.е. кроме элемента отвечающего источнику) наименьший, и подчёркиваем его. Из
выбираем среди элементов, отмеченных ^ (т.е. кроме элемента отвечающего источнику) наименьший, и подчёркиваем его. Из  убираем вершину, соответствующую подчёркнутому элементу (это В). Строим
убираем вершину, соответствующую подчёркнутому элементу (это В). Строим  . Для определения
. Для определения 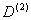 делаем вспомогательную запись: из матрицы W выписываем строку, соответствующую В, и прибавляем ко всем её элементам (кроме первого и второго) подчёркнутое число 5. Сравним полученные числа с
делаем вспомогательную запись: из матрицы W выписываем строку, соответствующую В, и прибавляем ко всем её элементам (кроме первого и второго) подчёркнутое число 5. Сравним полученные числа с 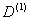 и в
и в 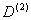 ставим на соответствующие места наименьшие:
ставим на соответствующие места наименьшие:  5 0 3 7 2 10
5 0 3 7 2 10
5 5 5 5
8 12 7 15, 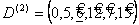 .
.
3 шаг. 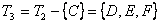 ,
, 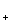 6 3 0 ∞ 7 ∞
6 3 0 ∞ 7 ∞
6 6 6
∞ 13 ∞, 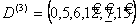 .
.
4 шаг. 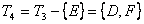 , ∞ 2 7 ∞ 0 4
, ∞ 2 7 ∞ 0 4
7 7 7
∞ 7 11, 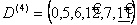 .
.
5 шаг. 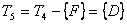 ,
, 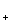 ∞ 10 ∞ 2 4 0
∞ 10 ∞ 2 4 0
11 11
13 11, 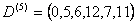 .
.
n=6, n-1=5, значит это последний шаг. По виду 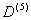 делаем вывод, что взвешенные расстояния от вершины А до остальных вершин равны
делаем вывод, что взвешенные расстояния от вершины А до остальных вершин равны 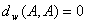 ,
,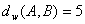 ,
, 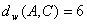 ,
, 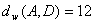 ,
, 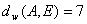 ,
, 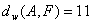 .
.
Алгоритм Дейкстры 2
Этот алгоритм (его иногда называют алгоритмом расстановки меток) позволяет найти не только вес кратчайшего пути, но и сам путь. Метки могут находиться в двух состояниях – быть временными и постоянными. Рассмотрим этот метод на том же примере. Дан граф на рисунке 3.4.4.
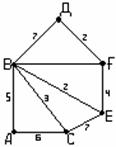
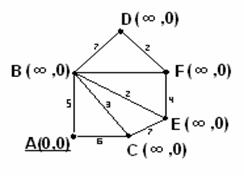
Рисунок 3.4.4 Рисунок 3.4.5
Найти кратчайшее взвешенное расстояние и путь от вершины А до вершины F.
1 шаг. Всем вершинам припишем метки 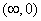 , вершине А – источнику - (0,0) и сделаем её постоянной и подчеркнём (рисунок 3.4.5).
, вершине А – источнику - (0,0) и сделаем её постоянной и подчеркнём (рисунок 3.4.5).
2 шаг. Рассмотрим смежные с А вершины В и С, т.к. вес 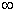 больше их расстояний (весов) от А, то заменяем
больше их расстояний (весов) от А, то заменяем 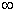 на эти расстояния 5 и 6, а вторую координату заменяем на А, т.е. получаем В(5,А) и С(6,А).
на эти расстояния 5 и 6, а вторую координату заменяем на А, т.е. получаем В(5,А) и С(6,А).
3 шаг. Выбираем минимальный из весов, приписанных В и С, – это 5. Поэтому вершину В(5,А) делаем постоянной, подчёркиваем (рисунок 3.4.6).
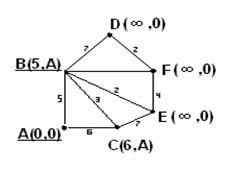
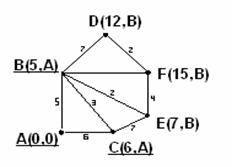
Рисунок 3.4.6 Рисунок 3.4.7
4 шаг. Как 2-ой шаг. Рассмотрим вершины, смежные с В(5,А), это C,D,E,F. Прибавим к их расстояниям от В вес вершины В: для С - 5+3=8, т.к. 8>6, то оставляем С(6,А); для D - 5+7=12, т.к. 12< 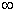 , то изменяем D(12,B);
, то изменяем D(12,B);
для E - 5+2=7, т.к. 7< 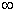 , то изменяем E(7,B); для F - 5+10=15, т.к. 15<
, то изменяем E(7,B); для F - 5+10=15, т.к. 15<  , то изменяем F(15,B).
, то изменяем F(15,B).
5 шаг. Как 3-ий шаг. Находим наименьшее из расстояний, присвоенных временным вершинам: min{6,12,7,15}=6, т.к. вершина С(6,А) имеет это расстояние, то делаем её постоянной, подчёркиваем (рисунок 3.4.7).
6 и 7 шаги. Как 2-ой и 3-ий шаги. Смежной с вершиной С будет только одна временная вершина Е(7,В), прибавим к её весу вес С: 7+6=13>7, итак, оставляем для Е те же координаты, делаем её постоянной, подчёркиваем (рисунок 3.4.8).
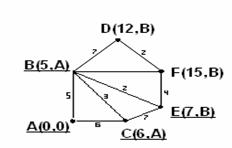
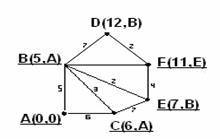
Рисунок 3.4.8 Рисунок 3.4.9
8 шаг. Смежной с Е временной вершиной будет F(15,B): 7+4=11<15, поэтому изменяем F(15,B) на F(11,E), делаем постоянной, подчёркиваем (рисунок 3.4.9).
Так как вершина F, до которой надо было найти кратчайший путь от А, стала постоянной, то процесс завершен. 11 есть кратчайшее расстояние от А до F. Если бы совокупность вершин, смежных с постоянной вершиной, была исчерпана до того, как мы достигли вершину F, то задача не имела бы решения, т.к. не было бы пути от А до F.
Для нахождения кратчайшего пути идём последовательно от F к А: F(11,E), Е(7,В), В(5,А), А (см. вторые координаты). Переставив вершины в обратном порядке, получим искомый путь: (A,B,E,F).
3.5 Лекция 13. Деревья. Лес. Минимальные остовые деревья
Содержание лекции: деревья, их свойства; остовые деревья; лес; минимальные остовые деревья.
Цели лекции: ввести новые понятия; отметить практическое значение нахождения остова минимального веса.
Деревья, лес, минимальные остовые деревья
Деревья являются самым распространённым классом графов, применяемых в программировании, это в некотором смысле простейший класс.
Определение.Деревом называется связный н-граф, не содержащий циклов; лесом называется несвязный н-граф без циклов.
Таким образом, компонентами связности любого леса являются деревья.
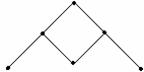
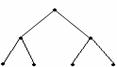
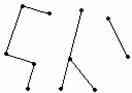 Пример 3.5.1 - На рисунке 3.5.1 а) изображено дерево; на рисунке 3.5.1 б) граф, не являющийся деревом; на рисунке 3.5.1 в) лес, состоящий из трёх деревьев.
Пример 3.5.1 - На рисунке 3.5.1 а) изображено дерево; на рисунке 3.5.1 б) граф, не являющийся деревом; на рисунке 3.5.1 в) лес, состоящий из трёх деревьев.
а) б) в)
Рисунок 3.5.1
Теорема (*). Пусть G – н-граф без петель, содержащий n вершин, тогда следующие условия эквивалентны:
а) G – ациклический граф, содержащий n-1 ребро;
б) любые две не совпадающие вершины графа G соединяет единственная простая цепь;
в) G – ациклический граф, такой, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Определение. Вершина v графа называется концевой (висячей, листом), если её степень 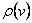 =1. Ребро инцидентное концевой вершине называется концевым.
=1. Ребро инцидентное концевой вершине называется концевым.
Любое дерево можно «подвесить» за какую-либо его вершину v, т.е. v расположить на верхнем этаже, смежные с ней вершины этажом ниже и т.д. (как на рисунке 3.5.2). В этом случае вершина v называется корнем дерева.
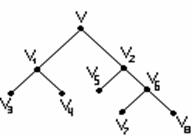
|
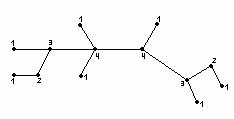 Рисунок 3.5.2 Рисунок 3.5.3
Рисунок 3.5.2 Рисунок 3.5.3
Все концевые вершины расположены на нижних этажах, они называются вершинами типа 1. Если из дерева удалить все вершины типа 1, то в оставшемся дереве концевые вершины называются вершинами типа 2 в исходном дереве. Аналогично определяются вершины типов 3, 4 и т.д. Конечное дерево имеет вершины лишь конечного числа типов, причём число вершин максимального типа равно 1 или 2. На рисунке 3.29 вершины v4, v3, v 5, v 6, v 7, v 8 – концевые, типа 1; v 1, v 6 – типа 2; v 2 – типа 3; v – типа 4.
Для каждого неориентированного дерева с корнем можно определить соответствующее ориентированное дерево с корнем: все рёбра такого дерева ориентируются от корня, причём данная ориентация единственная. При выборе другой вершины, корня, получается другой орграф-дерево.
Пример 3.5.2 - Рассмотрим граф-дерево на рисунке 3.5.3. Цифрами обозначены типы вершин. Таким образом, этот граф имеет две вершины максимального типа 4. Можно построить два различных ориентированных корневых дерева с корнем в вершине максимального типа: а) корень – левая вершина максимального типа 4 (рисунок 3.5.4); б) корень – правая вершина максимального типа 4 (рисунок 3.5.5).
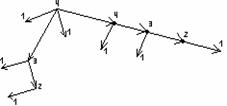
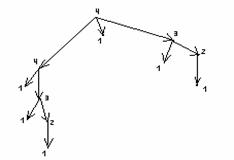
Рисунок 3.5.4 Рисунок 3.5.5
Если убрать ориентацию, то графы на трёх рисунках изображают одно и то же дерево.
Определение. Рассмотрим н-граф G=(V,E). Подграф 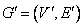 графа G называется остовом или каркасом графа G, если
графа G называется остовом или каркасом графа G, если 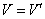 и
и 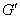 – лес, который на любой связной компоненте графа G образует дерево.
– лес, который на любой связной компоненте графа G образует дерево.
Если G связный граф, то его остов 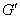 есть подграф графа G, являющийся деревом, которое называется остовым деревом.
есть подграф графа G, являющийся деревом, которое называется остовым деревом.
Очевидно, что в каждом графе существует остов, его можно получить, если разрушать в каждой связной компоненте циклы, удаляя лишние рёбра.
Пример 3.5.3 - Рассмотрим граф G, состоящий из двух связных компонент (рисунок 3.5.6). Рёбра обозначены цифрами. В качестве остова графа можно взять лес с рёбрами 2, 3, 4, 6, 7, удалив рёбра 1, 5, 8. Остов определяется неоднозначно, например, удалив рёбра 3, 5, 6, также получим лес, состоящий из двух остовых деревьев с рёбрами 2, 1, 4 и 7, 8.
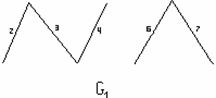
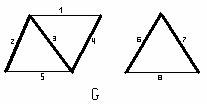
Рисунок 3.5.6
Теорема. Число рёбер произвольного н-графа G, которое необходимо удалить для получения остова, не зависит от последовательности их удаления, и равно m-n+к, где m – число рёбер, n – число вершин, к – число компонент связности графа.
Доказательство. Пусть Сi – і-ая компонента связности графа G (i=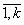 ). Пусть Сi содержит ni вершин. Тогда по теореме (*) её остовое дерево Кi будет содержать (ni -1) рёбер.
). Пусть Сi содержит ni вершин. Тогда по теореме (*) её остовое дерево Кi будет содержать (ni -1) рёбер.
Если mi – число рёбер Сi, ni -1– число рёбер Кi, то для получения Кi из Сi нужно удалить (mi-(ni -1))= mi - ni +1 рёбер. Всего компонент связности к, поэтому, суммируя все удалённые рёбра по всем компонентам связности графа G, получим: 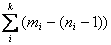 =
= 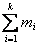 -
- 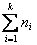 +
+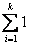 =m-n-к.
=m-n-к.
Определение.Число ν(G)=m-n+к называется цикломатическим числом(илицикломатическим рангом) графа G. Число 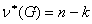 называется коциклическим рангом или корангом. Таким образом,
называется коциклическим рангом или корангом. Таким образом, 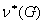 - это число рёбер, входящих в любой остов графа G.
- это число рёбер, входящих в любой остов графа G.
Следствия: а) н-граф G является деревом (лесом) тогда и только тогда, когда ν(G)=0; б) н-граф G имеет единственный цикл тогда и только тогда, когда ν(G)=1.
Число остовов в графе можно найти с помощью матрицы Кирхгофа, которая определяется так: 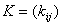 где
где 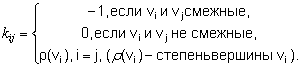
Теорема Кирхгофа.Число остовых деревьев в связном графе, имеющем n вершин (n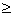 2), равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
2), равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Пример 3.5.4 - Для графа на рисунке 3.5.7 степени вершин будут равны
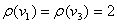 ,
, 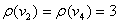 .
. 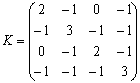 - матрица Кирхгофа.
- матрица Кирхгофа.
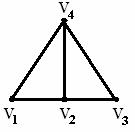
Рисунок 3.5.7
Рассмотрим, например, алгебраическое дополнение элемента 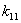 :
:
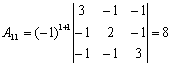 . Таким образом, существует 8 остовых деревьев графа.
. Таким образом, существует 8 остовых деревьев графа.
Определение остового дерева минимального веса
Вес остового дерева взвешенного графа G равен сумме весов, приписанных рёбрам остового дерева. Остов минимального веса (или минимальное остовое дерево) – это такой остов графа G, что его вес меньше или равен весу любого другого остова графа.
Задача определения остова минимального веса (кратчайшего остова) имеет множество практических применений. Она возникает, например, при проектировании линий электропередач, дорог, телеграфных линий, авиалиний и т.д., когда требуется заданные центры (вершины) соединить некоторой системой каналов связи (рёбер), так, чтобы два центра были связаны либо непосредственно, либо через другие центры (цепью) и чтобы общая длина (или стоимость, или другой вес) каналов связи была минимальной.
Рассмотрим алгоритм Краскала (Крускала) построения остова минимального веса. Идея этого метода следующая: дан граф G=(V,E), будем формировать дерево T=(V,En-k), выбирая рёбра с наименьшим весом так, чтобы не возникало циклов:
1. Строим граф  , состоящий из множества вершин V и ребра
, состоящий из множества вершин V и ребра  , которое имеет наименьший вес (т.е.
, которое имеет наименьший вес (т.е. 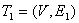 , где
, где 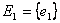 ).
).
2. Если граф 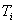 уже построен и
уже построен и 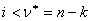 , то строим граф
, то строим граф 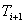 добавляя к множеству рёбер
добавляя к множеству рёбер 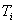 ребро
ребро 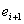 , имеющее наименьший вес среди рёбер, не входящих в
, имеющее наименьший вес среди рёбер, не входящих в 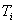 и не составляющее циклов с рёбрами
и не составляющее циклов с рёбрами 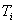 (т.е.
(т.е. 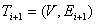 , где
, где 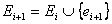 ).
).
3. При 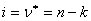 алгоритм закончен и
алгоритм закончен и 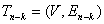 - есть остов минимального веса, его вес равен сумме весов всех его рёбер.
- есть остов минимального веса, его вес равен сумме весов всех его рёбер.
Пример 3.5.5 - Дан взвешенный граф (рисунок 3.5.8). Построить остов
минимального веса и найти его вес:
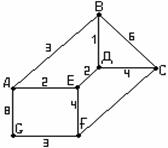
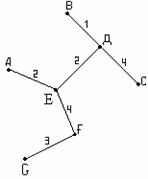
Рисунок 3.5.8 Рисунок 3.5.9
а) 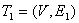 , где V ={A,B,C,D,E,F,G},E1={{B,D}};
, где V ={A,B,C,D,E,F,G},E1={{B,D}};
б) 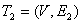 , E2={{B,D},{E,D}};
, E2={{B,D},{E,D}};
в)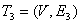 , E3={{B,D},{E,D},{A,E}};
, E3={{B,D},{E,D},{A,E}};
г) 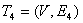 , E4={{B,D},{E,D},{A,E},{E,F}};
, E4={{B,D},{E,D},{A,E},{E,F}};
д) 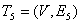 , Е5={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}};
, Е5={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}};
е) 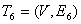 , E6={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}, {C,D}}.
, E6={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}, {C,D}}.
Число вершин графа n=7, число компонент k=1, число рёбер m=10, коранг 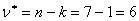 , значит, остов должен содержать 6 рёбер, удалено ν=m-n+к=10-7+1=4 ребра. Алгоритм закончен, построено дерево минимального веса (рисунок 3.5.9). Его вес равен 1+2+2+4+3+4=16.
, значит, остов должен содержать 6 рёбер, удалено ν=m-n+к=10-7+1=4 ребра. Алгоритм закончен, построено дерево минимального веса (рисунок 3.5.9). Его вес равен 1+2+2+4+3+4=16.
Заметим, что если множество Т содержит более одного дерева, то существует ребро, при добавлении которого не возникает цикла – оно соединяет два дерева. Добавленное ребро - кратчайшее возможное (в примере 3.5.5 ребро {E,F} соединило два дерева).
Список литературы
1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной
математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002.- 280 с.
2. Москинова Г.И. Дискретная математика. Математика для менеджера
в примерах и упражнениях: Учебное пособие. – М.: Логос, 2004. – 240 с.
3. Новиков Ф.А. Дискретная математика для программистов. Учебник
для вузов. 2-е изд. – СПб.: Питер, 2004. – 364 с.: ил. – (Серия «Учебник для вузов»).
4. Андерсон, Д. Дискретная математика и комбинаторика.: Пер. с англ.
– М.: Издатель- ский дом «Вильямс», 2004. – 960 с.: ил. – Парал. тит. англ.
5. Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: изд-во
МГТУ им. Н.Э.Баумана, 2001
6. Шапорев С.Д. Дискретная математика. Курс лекций и практических
занятий. – СПб.: БХВ-Петербург, 2006.- 396 с.
7. Яблонский С.В. Введение в дискретную математику. – М. «Высшая
школа», 2001
8. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика:
Учебное пособие.- Ростов н/Д: «Феникс»6 Харьков: «Торсинг», 2003. -144 с.
9. Плотников А.Д. Дискретная математика: учебное пособие/
А.Д.Плотников. – 2-е изд., испр. и доп. – М.: Новое знание, 2006.– 304 с.
10. Оре О. Графы и их применение: пер. с англ./ Под ред. и с предисл.
И.М.Яглома. Изд. 3-е, стереотипное. –М.: КомКнига, 2006. – 168 с.


Содержание
1 Элементы теории множеств
Лекции 1-3
1.1 Множества
1.2 Алгебра множеств
1.3 Отношения
1.4 Отношение эквивалентности
1.5 Отношение порядка
1.6 Функциональные отношения (функции)
1.7 Понятие мощности множств
2 Элементы математической логики
Лекции 4-7
2.1 Логика высказываний
2.2 Алгебра логики
2.3 Эквивалентность формул. Основные эквивалентные соотношения
алгебры логики
2.4 Булева алгебра логических функций. Полные системы
логических функций
2.5 Дизъюнктивные и конъюнктивные нормальные формы
2.6 Минимизация булевых функций в классе ДНФ. Карты Карно
2.7 Двойственность
2.8 Булева алгебра и теория множеств
2.9 Коммутационные схемы
3 Элементы теории графов
Лекции 8-13
3.1 Основные понятия и определения
3.2 Изоморфизм графов
3.3 Операции над графами
3.4 Маршруты, достижимость, связность
3.5 Исследование маршрутов графа
3.6 Нахождение кратчайших маршрутов (путей)
3.7 Деревья, лес, минимальные остовые деревья
3.8 Определение остового дерева минимального веса
Список литературы
|
Дата добавления: 2014-01-15; Просмотров: 1529; Нарушение авторских прав?; Мы поможем в написании вашей работы!