Дифференциальные уравнения в форме Коши

Задача Коши. Задача Коши, как известно из курса математики, состоит в задании системы дифференциальных уравнений в нормальной форме (разрешенных относительно первой производной) и задании для них граничных (начальных) условий в одной точке.

Использование формы Коши определяется тем, что при решении дифференциальных уравнений удобнее иметь дело не с уравнениями высокого порядка (выше первого), а с системами уравнений первого порядка.

Рассмотрим скалярный объект, поведение которого в динамике описывается дифференциальным уравнением n -го порядка

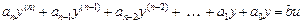. (2.17)

Произведем в этом уравнении замену переменных следующим образом:

(2.18)

и разрешим исходное уравнение относительно старшей производной

или

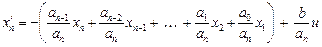. (2.19)

Совокупность уравнений (2.18) и (2.19) представляют нормальную форму Коши дифференциального уравнения (2.17). В общем виде полученная система представляется как

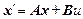, (2.20)

где

есть матрица Фробениуса, а матрица

определяет влияние входного воздействия на состояние объекта.

Значение выходного сигнала y объекта определяется в общем случае как состоянием объекта x, так и значением входного воздействия u, так что

.

В общем случае А − функциональная матрица размером n × n, называемая матрицей состояния системы (объекта), В − функциональная матрица размером n × r, называемая матрицей управления (входа), С − функциональная матрица размером m × n, называемая матрицей выхода по состоянию, D − функциональная матрица размером m × r, называемая матрицей выхода по управлению.

Очень часто D = 0, т.е. выход непосредственно зависит от входа и тогда исходная система уравнений приобретает вид:

(2.20)

Пример 2.6. Представить дифференциальное уравнение

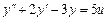
в форме Коши.

Решение. Вводим новые переменные:

,

откуда с учетом исходного уравнения следует

Таким образом, представление исходного уравнения в виде (2.20) приводит к формированию следующих матриц:

■

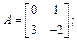
Пример 2.7. Преобразовать полученное дифференциальное уравнение второго порядка для механическойсистемы (рис. 2.7) в форму Коши.

Решение. Заменим наблюдаемую переменную y на переменную состояния x ₁:

. (2.21)

Тогда уравнение (2.8) примет следующий вид:

(2.22)

Если уравнение (2.22) разделить относительно производных и проинтегрировать по времени, получим уравнение первого порядка

.

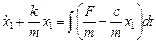Обозначим

. (2.23)

Продифференцируем последнее выражение

. (2.24)

В итоге получилось два уравнения первого порядка (2.23) и (2.24), дающие описание динамики системы. Совокупность полученной системы уравнений

(2.25)

совместно с уравнением (2.21), называемым уравнением наблюдения, составляет полное описание поведения объекта в форме Коши.

■

Пример 2.8. Перейти к стандартной форме Коши для рассмотренной выше электрической системы (рис. 2.1), описываемой системой уравнений:

;

.

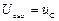Решение. Пусть

; ,

тогда из второго уравнения получаем

.

Используя теперь полученное соотношение, запишем первое уравнение в виде

.

В результате получаем систему из двух уравнений первого порядка:

с уравнением наблюдения

.

■

Пример 2.9. Рассмотрим полученную выше систему дифференциальных уравнений механической системы (1.45):

,

и представим ее в матричной форме. Она должна принять вид (2.20), где – вектор состояния, размерности 2; u – в данном случае скалярное управление (в общем случае это тоже вектор); y – в данном случае, также скалярное наблюдение (в общем случае – также вектор).

Сравнивая исходную систему уравнений и конечную форму, видим, что

,

следовательно, исходная система уравнений запишется в матричной форме в виде:

Для решения этой системы уравнений не хватает начальных условий, которые, конечно же, существуют, но не обязательно известны исследователю. Будем считать, что начальные условия известны, и они заданы в одной точке:

Пример 2.10. Получим уравнения состояния для простейшей RLC -цепи, показанной на рис 1.21. Динамическое поведение этой системы при t ≥ t ₀ полностью определяется, если известны начальные значения i (t ₀), U _c(t ₀) и входное напряжение U (t). Следовательно, и можно выбрать в качестве переменных состояния, то есть , . Тогда совокупность исходных уравнений:

может быть представлена в виде

Полученные дифференциальные уравнения можно записать в векторно-матричной форме:

.

Таким образом для рассматриваемой системы матрицы А, В, С векторно-матричной модели будут иметь следующий вид:

; ; .

■

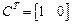Матричное описание строго формализовано, и не требует понимания физической природы системы. Также структура модели в "пространстве состояний" не позволяет разобраться во внутренней природе системы. Если эта форма записи дифференциальных уравнений применена обоснованно, то модель, скорее всего, будет истинной.

Дата добавления: 2014-01-15