Общая постановка задачи. Опорным решением задачи называется допустимое неотрицательное решение

Лекция 3

3. СИМПЛЕКСНЫЙ МЕТОД

Опорным решением задачи называется допустимое неотрицательное решение. Идея симплексного метода заключается в том, что, начиная с некоторого исходного опорного решения, осуществляется последовательно направленное перемещение по опорным решениям задачи к оптимальному решению.

3.2. Алгоритм симплексного метода

1. Математическая модель должна быть канонической. Если она неканоническая, то её надо привести к каноническому виду.

2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу. Все строки таблицы 1-го шага, за исключением строки ∆_j заполняем по данным системы ограничений и целевой функции:

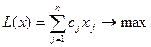
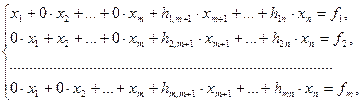
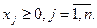
Таблица 3.1

сi	БП	с1	с2	…	cm	cm+1	…	cn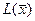
x1	x2	…	xm	xm+1	…	xn	bi
c1	x1	1	0	…	0	h1,m+1	…	h1n	f1
c2	x2	0	1	…	0	h2.m+1	…	h2n	f2
…	…	…	…	…	…	…	…	…	…
cm	xm	0	0	…	1	hm,m+1	…	hmn	fm
	∆j	0	0	…	0	∆m+1	…	∆n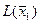

Индексная строка для переменных находится по формуле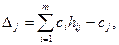

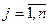
и по формуле 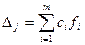для свободного члена.

Возможны следующие случаи при решении задачи на максимум:

- если все оценки 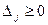, то найденное решение оптимальное;

- если хотя бы одна оценка 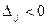, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращаем, так как 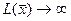, т. е. целевая функция неограниченна в области допустимых решений;

- если хотя бы одна оценка отрицательна, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;

- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Если хотя бы одна оценка , то к -й столбец принимаем за ключевой. За ключевую строку принимаем ту, которой соответствует минимальное отношение свободных членов (f_i) к положительным коэффициентам к -го столбца. Элемент, находящийся на пересечении ключевой строки и ключевого столбца, называется ключевым элементом.

3. Заполняем симплексную таблицу 2-го шага:

- переписываем ключевую строку, разделив её на ключевой элемент;

- заполняем базисные столбцы;

- остальные коэффициенты таблицы находим по правилу «прямоугольника». Оценки можно считать по приведённым выше формулам или по правилу «прямоугольника». Получаем новое опорное решение, которое проверяем на оптимальность, и т. д.

Правило «прямоугольника» заключается в следующем. Пусть ключевым элементом 1-го шага является элемент 1-й строки (m+1)-го столбца h_1,m+1. Тогда элемент i -й строки (m+2)-го столбца 2-го шага – обозначим его 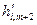согласно правилу «прямоугольника» выражается формулой

,

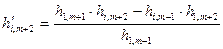где h_i,m+2, h_i,m+1, h_1,m+1 – элементы 1-го шага.

Примечание 1. Если целевая функция 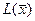требует нахождения минимального значения, то критерием оптимальности задачи является следующее условие: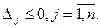

Примечание 2. Если в правой части какого-нибудь неравенства из системы ограничений стоит отрицательное число, то обе части этого неравенства нужно разделить на (-1), а потом приводить это неравенство к каноническому виду.

Примечание 3. Пусть модель каноническая, но нет переменных, которые можно использовать в качестве базисных (т. е. таких, которые в одном уравнении стоят с коэффициентом 1, а в других вообще отсутствуют). Тогда нужно по своему усмотрению выбирать базисные переменные, определять ключевой столбец и строку, пересчитывать элементы таблицы по правилу «прямоугольника», не заполняя оценочной строки. Это нужно проделывать до тех пор, пока не будут найдены все базисные переменные. Затем заполнить оценочную строку и определить, является ли найденное решение оптимальным. Если нет, то пересчитать таблицу.

Дата добавления: 2014-01-15