Марковские цепи

Марковский случайные процесс с дискретными состояниями и дискретным временем называют Марковской цепью. Для такого процесса моменты 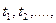, когда система S может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, номер шага 1, 2, ….., k, … Случайный процесс в этом случае характеризуется последовательностью состояний S(0), S(1), S(2),…..,S(k),…, где S(0)- начальное состояние системы (перед первым шагом); S(1)- состояние системы после первого шага; S(k)- состояние системы после k-го шага…

Событие {S(k)=Si}, состояние в том, что сразу после k-го шага система находится в состоянии Si(i=1,2,…), является случайным событием. Последовательность сосотояний S(0), S(1), S(2),…..,S(k),… можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния Si в любом Sj не зависит от того, когда и как система пришла в состояние Si. Начальное состояние S(0) может быть заданием заранее или случайным.

Вероятностями состояний цепи Маркова называются вероятности того, что после k-го шага (и до (k+1)-го) система S будет находиться в состоянии Si(i=1,2,…,n). Очевидно, для любого k

Начальным распределением вероятностей Марковской цепи называется распределение вероятностей состояний в начале процесса:

P1(0),P2(0),…..,Pi(0),…,Pn(0).

В частном случае, если первоначальное состояние системы S в точности известно S(0)= Si, то начальная вероятность Pi(0)=1, а все остальные равны нулю. Вероятность перехода на k-м шаге из состояния Si в состояние Sj при условии, что непосредственно перед этим она находится в состоянии Si. Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать 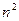вероятностей перехода Pij, которое удобно представить в виде следующей матрицы:

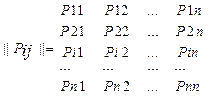
где Pij- вероятность перехода за один шаг из состояния Si в состояние Sj, Pii- вероятность задержки системы в состояние Si.

Матрица называется переходной или матрицей переходных вероятностей. Если переходные вероятности не зависят от номера шага, а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь Маркова называется однородной. Переходные вероятности однородной Марковской цепи Pij образуют квадратную матрицу размера n*n. Отметим некоторые ее особенности:

1. Каждая строка характеризует выбранное состояние системы, а ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и переход в самое себя.

2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное состояние (иначе говоря, строка характеризует вероятность перехода системы из состояния, столбец -в состояние).

3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:

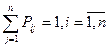
4. По главной диагонали матрицы переходных вероятностей стоят вероятности Pii того, что система не выйдет из состояния Si, а останется в нем.

Если для однородной Марковской цепи заданы начальное распределение вероятностей и матрица перехода вероятностей ||Pij||, то вероятности состояний системы Pi(k) ().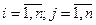

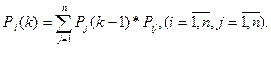
Тема 3. Метод Монте – Карло.

Метод Монте-Карло как разновидность имитационного моделирования. Датой рож­дения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают амери­канских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опублико­ваны в 1955—1956гг.

Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ.

Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом.

Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас».

Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс - явно немарковский, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным).

В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)³ = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опытсчитается«удачным», если хотя бы на одной из монетвыпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен.

Метод Монте-Карло- это численный метод решения математических задач при помощи моделирования случайных величин.

Дата добавления: 2014-01-15