Быстродействие и время регулирования

1. tg; t= k=1,2,3… коэффициент, определяемый исходя из перерегулирования (σ)

2. Перерегулирование зависит от длины среднечастотного участка w₂÷w₃- 20дб/дек. При длине < 2 декад появляется погрешность перерегулирования, зависящая от и 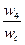. Если w₃-w₂≈2 декадам, то σ =0

Низкочастотный участок w≤w₁ не сказывается на качестве переходного процесса, но определяет точность в установившемся режиме.

-20дб/дек ν=1 система астатическая первого порядка

-40дб/дек ν=2

0 ν=0

Высокочастотный участок w>w₄ практически не оказывает влияния на время переходного процесса L(w)<-25дб/дек

55. Интегральные оценки качества

Эти оценки позволяют связать в единый показатель точность в установившемся режиме и качество переходного процесса. Пусть имеется замкнутая система

V(t)=1(t) y(t)=h(t)

x(t)=y_ycm-y(t)= h_ycm-h(t) h_ycm=Ф(0)

y_ycm установившееся значение переходной характеристики

Интегральной оценкой качества называются различные интегралы от функции x(t). Интегральная оценка будет определять некоторую площадь от кривой.

1. Простейшей оценкой является линейная оценка.

I₁= соответствует площади подл кривой.

Если x(t) монотонная функция, не меняющая знак, то этот интеграл будет состоятельной оценкой качества переходного процесса.

Оценка I₁ просто считается.

Пусть х(S)= 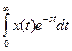положим, что S=0, то I₁= x(0) x(S)=(Ф(0)-Ф(S))

Если представит Ф(S) как отношение двух многочленов

Х(S)=

Недостатками оценки является то, что при колебательном S(t) оценка I₁становится несостоятельной, так как из её малости не следует малость модуля площади под кривой x(t). Состоятельной оценкой была бы следующая оценка:

I₁₁=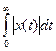 Она состоятельна как для монотонных, так и для колебательных процессов, но связать её с передаточной функцией с помощью простых выражений не удается.

2. Квадратическая оценка

I₂= Эта оценка подчеркивает большие оценки. Оценка является состоятельной для колебательных процессов.

Её вычисление в конечном итоге сводится к интегралу Релея.

I₂== Интеграл Релея приводится в приложениях. Рассмотрим связь I₂ с параметром передаточной функции.

x(jw)=[Ф(0)-Ф(jw)]

Рассмотрим случай астатичесой системы ν=1,2… Ф(0)=1; для них Ф(0)-Ф(jw)-Ф_с(jw)

I₂ для астатических систем можно посчитать следующим образом:

I₂=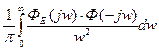

Как I₁, так и I₂ достаточно вычислить в общем виде через параметры передаточной функции. При анализе систем часть параметров является неизменяемыми, заданными, а часть их можно менять.

Для простоты предположим, что передаточная функция имеет 2 параметра α и β, тогда

I=I(α, β) α[ α_min;α_max] β[ β _min;β _max]

Обычно знак параметров выбирают так, чтобы I→minh(t) →h наиболее близко к идеальному переходному процессу. Для нахождения минимумов можно взять условие экстремумов:

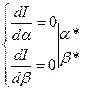Если α* и β* внутренние точки интервала допустимого α_допβ_доп, тогда можно найти I₂(α*, β*), если нет, то нужно воспользоваться граничным значением. Рассмотрим процедуру минимизации оценок параметров синтезом. Она позволяет при известной структуре системы выбрать наилучшее значение параметров с учетом ограничений. Практика применения такого метода определяет оптимальных параметров при минимизации I₂ показала, что переходные процессы при оптимальных параметрах могут получаться слишком колебательными. В этом случае возникает задача ограничить колебательность за изменения оценки I₂. В результате такой модуляции получается оценка I₂₁

I₂₁=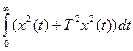

В оценку I₂₁ входит также интервал, характеризующий скорость изменения колебательного процесса. Поэтому с учётом члена Т(t) будет минимизация и скорость колебательного процесса. В этом случае оптимум процесса будет другой. Найдем оптимум процесса, соответствующий I₂ →min

I₂₁=

Условие минимума будет следующим

T однородное ДУ. Его решение х*(t)=x0e-t/T, где T - постоянная времени, которая выбирается исходя из определённых соображений.

Монотонному процессу х(t) будет соответствовать монотонный процесс h*(t)

h*(t)=h_ycm(1-e-t/T) h*- переходная характеристика апериодического звена.

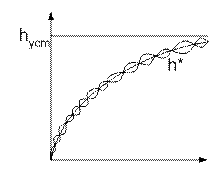
Вычисление интеграла I₂ несколько более сложное. Для получения более гладких переходных процессов в оценку I₂₁ включают члены, содержащие вторую и более высокие производные.

Чувствительность систем.

56. Функции чувствительности.

Предположим, что система описана ДУ:

x(t) – координаты состояний

- вектор изменения параметров

- номинальные значения параметров, которые в процессе работы системы могут принимать различные значения

Δα₁,…,Δα_m – отклонения

При номинальных параметрах:

При измененных параметрах:

- возмущенное решение

- невозмущенное решение при номинальных значениях

, где R₂(Δα_j²) – остаточный член,

Функция чувствительности, определяемая при номинальных значениях параметров: , где U_{i j}, образует матрицу n*m

Таким образом, если отклонения Δα параметров невелики, то остаточным членом можно пренебречь:

,

Находить функции чувствительности в виде производных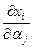обычно затруднительно.

При больших n, для изучения функции чувствительности, их задают решением специальных ДУ, которые называют ДУ чувствительности:

Продифференцируем левую и правую части уравнений:

, ,

Уравнения чувствительности для нелинейных систем:

, ,

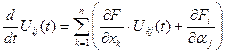Если исходная система описывается линейным ДУ, то система все равно получается нелинейной. Для решения систем используются только численные методы и методы моделирования.

Коррекция систем.

57. Общие сведения о коррекции.

Систему, составленную из необходимых элементов, и имеющую коэффициент усиления в разомкнутой системе k = k_тр и порядок астатизма υ = υ_тр, называют нескорректированной. Эта система, имея требуемую точность обработки установленного сигнала, не обладает требуемым показателем качества переходных процессов, т.е. просто неустойчива. Возникает задача коррекции нескорректированных систем. Цель коррекции – придание системе таких свойств, при которых она обладает требуемым показателем качества переходных процессов. Коррекция осуществляется с помощью дополнительной коррекции устройств. При описании системы вход – выход корректирующие устройства могут включаться в систему либо последовательно в цепь прямой передачи сигнала, либо параллельно, охватывая один или несколько функционально необходимых элементов (цепь МОС).

При описании системы коррекция осуществляется в виде обратных связей по состоянию.

58. Последовательная коррекция

1.Пусть задана нескорректированная система

W_нс(s) – передаточная функция нескорректированной системы

а)

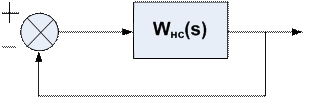
б)

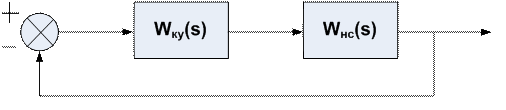
При включении системы – корректир. сист.

W_ск(s) = W_ку(s) *W_нс(s)

Наиболее удобно последовательную коррекцию изучать с помощью ЛЧХ:

L_ск(ω) = L_ку(ω) + L_нс(ω)

φ_ск(ω) = φ_ку(ω) + φ_нс(ω)

Коррекцию аналоговых систем удобно осуществлять с помощью типовых RC-соединений:

1. дифференциальный контур

2. интегральный контур

3. интегро-дифференциальный контур

Рассмотрим возможности коррекции в каждом из контуров:

дифференциальный контур

W_дк(s) = R₂/=

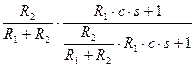
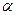= ; W_дк(s) =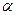

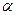<1; T = R₁*c

ЛЧХ: arctg(ωT) – arctg(αωT)

Уменьшение коэффициента усиления недопустимо, т. к. к = к _треб. При включении дифференциального контура необходимо увеличить коэффициента усиления каскада усилителей так, чтобы общий коэффициент усиления остался неизменным. Сигнал U₁ будет содержать шумовые высокочастотные составляющие. Величину α ограничивают, чтобы сигнал не затерялся в шумах (α0.2; ). Увеличение ω_с, φ(ω) происходит за счет положительного φ_дк (ω).

Правильно подобранный контур позволяет увеличить быстродействие, но уменьшает помехоустойчивость.

интегрирующий контур:

W(s) = = ; T₁=R₁*c; T₂=(R₁+R₂)*c; T₁<T₂
ЛЧХ:

φ(ω) = arctg(ωT₂) + arctg(ωT₁)

Контур пропускает низкочастотные составляющие, оставляет высокочастотные составляющие входного сигнала, в том числе помехи, поэтому контур высоко помехозащищен. Запаздывание по фазе φ(ω) увеличивается за счет уменьшения ω_с, уменьшается быстродействие системы, что ведет к увеличению времени регулирования.

интегро-дифференциальный контур:

W(s) =

T₁ = R₁*C₁; T₂ = R₂*C₂; T₃*T₄ = T₁*T₂

T₃ + T₄ = R₁*C₁ + R₂*C₂ + R₁*C₂

T₄ > T₁ > T₂ > T₃

Правильно подобранный интегро-дифференциальный контур позволяет уменьшить коэффициент передачи в области средних частот, почти не меняя ω_с, и обеспечивает положительный сдвиг по фазе в области частоты среза. Можно воспользоваться 2-мя корректирующими условиями.

где РУ – развязывающее устройство,

R_вх - велико

59. Параллельная коррекция

W_охв (s) – функция преобразования элементов, охваченных МОС

W_β (s) – функция преобразования параллельного КУ

W_ск(s) = W1(s)=

W_{к экв}(s) =

Последовательному КУ будет соответствовать некоторое параллельное КУ и наоборот.

В зависимости от свойств W_β (s), МОС делят на жесткие и гибкие:

ЖОС: W_β (0) 0

ГОС: W_β (0) = 0

Примеры:

1. Охват усилителя с большим К_охв:

W_куэ = ,

W_куэ = , W_β (s) = T₁S +1

2. Охват апериодического звена ЖОС:

W_э(s) = =

Т₁ = ; К₁ =

Уменьшение коэффициента усиления

нетрудно скомпенсировать за счет

усилителя.

3. Охват последовательно соединенных апериодического и интегрирующего звеньев ЖОС:

W_э = =

Соединение стало статическим.

4. Охват апериодического и интегрирующего звеньев ГОС:

W_э =

T₁ =

5. Оценка коррекции по ЛЧХ:

Сложные выражения: W_охв (s) и W_ку (s) W_кэ (s)

W_ск(s) =

L_ск(ω) = L_нс(ω) – 20 lg

Ľ₂(ω) = 20 lg

Ľ₂(ω) =

По рассмотренной методике решают задачи разработки систем с заданными свойствами, задачи синтеза. В общем случае задача синтеза сложна и не получила своего окончательного решения для линейных стационарных систем. Поэтому синтез осуществляется не как нахождение некоторой наилучшей системы, а как реализация желаемой системы. После выбора этой системы решается задача коррекции нескорректируемой системы с тем, чтобы приблизить скорректированную систему к желаемой. При этом в самих системах для коррекции может использоваться обратная связь по состоянию.

60. О модальном регулировании

x` = Ах(t) + BU(t) x(t) R_n; U(t) R_m

y(t) = Cx(t) (1) y(t)R_e

Для управления этой системой можно использовать сигнал U(t) = V(t) – F*x(t) (2)

(1) – уравнение разомкнутой системы

(2) – принимает вид для замкнутой системы

V(t) – задающий сигнал, F*x(t) – сигнал ОС

(3)

AA_R = A – BF – системная матрица замкнутой системы

rank R =

если (А, В) – полностью управляема, то F – регулятор

det (sI - A_R) = 0

S_i*(A_R) – наперед заданные корни

Модальное регулирование – управление расположением мод замкнутой системы

F – модальный регулятор

Это управление удобно реализовать, если вектор состояния x(t) имеет измер. координаты состояния. Реализация модального управления наводит на непреодолимые затруднения. Вместо модального управления, матрицу F выбирают как стабилизирующую управлением.

det (sI - A_R) = 0

S_i (A_R): I =, ReS_i(A_R) устойчивость с запасом

δ – степень устойчивости

Дискретные системы

61. Общие сведения о дискретных системах

Система называется дискретной, если хотя бы один из сигналов имеет дискретную форму (импульсная или цифровая). При автоматическом управлении все объекты управления являются аналоговыми, поэтому структуру дискретной системы можно рассматривать в виде:

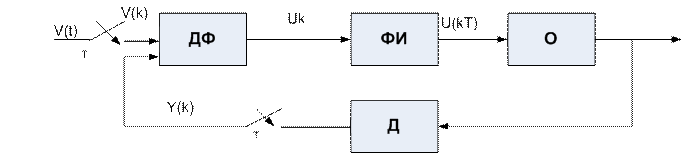
ДФ – дискретный фильтр

ФИ – формирователь импульсов управления

О – объект управления

Д – аналоговый датчик

ключ:

Т – период замыкания ключа на бесконечномалое

время

Решетчатая функция:

V(0) = V(t), t = 0

V(1) = V(t) и т.д.

V(k) =

V(t)V(kT) = V(k) = V_k

Аналогичным преобразованиям подвергается сигнал y(t)y(k)

Если дискретный фильтр является импульсным устройством, то он оперирует разностью: ε(k) = V(k) – y(k)

Если ДФ – цифровое устройство, то будем считать, что ε(k)ε*(k)

Разрядность кода достаточно велика, т.е. шаг квантования мал. Это позволяет одинаково анализировать как импульс, так и цифровой системы.

Для цифрового сигнала ФИ – это ЦАП.

U(kT) =

0

ЦАП можно рассматривать как ФИ при σ = 1

Для анализа подобных систем используются дискретные модели, которые позволяют определить зависимость между отдельными отсчетами.

y(t) kT

y(k,ε) = y ((k+ε)T) смещенная решетчатая функция:

62. Разностные уравнения

f(t) f(kT) = f(k), k = 0, 1, 2

f́ (t) ~ Δ f(k) = f(k+1) – f(k) – классическая разность вперед

f(k) = f(k) – f(k-1) - классическая разность назад

f ″(t) ~ Δ² f(k) = Δ f(k+1) – Δ f(k) = f (k+2) – 2f(k+1) + f(k)

f ^m (t) ~Δ^m f (k) =

Дифференциальным уравнениям будут соответствовать разностные уравнения:

(1) C₀ y(k+n) + C₁ y(k+n+1) +…+ C_n-1 y(k+1) + C_n + y_k = b₀ V(k+m) + b₁ V(k+m+1) +…+ b_m V(k)

(2) C₀ y(k) + C₁ y(k - 1) + …+ C_n y(k - n) = b₀ V(k+m–n) +…+ b_m V(k - n)

Чтобы решить эти уравнения, необходимо задать начальные условия:

y(k+n-1), …, y(k) – вектор начальных условий

y(k - 1), …, y(k - n) – аналогично

Рассмотрим однородные разностные уравнения:

C₀ y(k) + C₁ y(k - 1) + …+ C_n y(k - n) =0

y(k) = С₁Z+ С₂Z+ …+ С_nZ

где Z_i – корни характеристического уравнения C₀Zⁿ + C₁Z^n-1 + …+ C_n = 0, i =

C_i – произвольная постоянная из вектора НУ, i =

Если определен вектор НУ, то разностные уравнения можно решить рекуррентно.

y(k)→0, k→∞,

Равномерная асимптотическая устойчивость:

63. Z – Преобразование.

Преобразование Лапласа позволяет алгебраизовать дифференциальные уравнения. Для дискретных систем аналогичную роль играет Z – преобразование, которое алгебраизовывает разностные уравнения. Z – преобразование получают путем модификации преобразования Лапласа для решетчатых функций.

F*

e^sT = Z

Z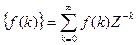 - Z – преобразование решетчатой функции

Z – преобразование обладает следующими свойствами:

1. преобразование линейно

f(t) =

2. изображение простейших функций

δ(k) – играет роль δ – функции для аналогичных сигналов

f(k) = δ(k) =

Z{ δ(k)} = 1*Z⁰ = 1

f(k) = 1(k) = 1, k = 0, 1, 2,…

3. Z{1(k)} = 1*Z⁰ + 1*Z^-1 + … =

f(k) = kT, k = 0, 1, 2,…

Z{kT} = T(0* Z⁰ + 1*Z^-1 + 2*Z^-2 + …) = TZ^-1(1 + 2 Z^-1 +3 Z^-2 + …) = TZ^-1(1 + Z^-1 + Z^-2 + …) = =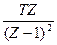

f(k)

Z{f(k+1)} -?

Z{f(k+1)} = f₁* Z⁰ + f₂* Z^-1 +… = Z⁺¹{ f₁* Z^-1 + f₂* Z^-2 + … + f₀ - f₀} = Z*F(Z) - f₀

F(Z) = f₁* Z^-1 + f₂* Z^-2 + … + f₀

f(0) = 0, Z – оператор сдвига на 1 период квантования

Z{f(k-1)}= Z^-1F(Z)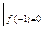

Передаточные функции дискретных систем.

64. Передаточная функция дискретного фильтра.

α₀ y(k+n) + α₁ y(k+n-1) +…+ α_n y(k) = β₀ ε(k+m) + β₁ ε (k+n-1) +…+ β_m ε(k) (1)

Преобразуем левую и правую части разностного уравнения (1) с помощью Z – преобразования:

(α₀*Zⁿ + α₁*Z^n-1 + … + α_n) y(Z) = (β₀*Z^m + β₁*Z^m-1 + …+ β_m) E(Z)

W_дф(Z) = - ПФ дискретного фильтра

C(Z) = , B(Z) =

ПФ дискретного фильтра является полным аналогом передаточной функции непрерывных систем:

C(Z) = 0, Z_i, i = - полюсы ПФ

B(Z) = 0, r_i, i = - нули ПФ

65. Передаточная функция формирователя импульсов и объекта.

U(kT) =

Для определения ПФ формирователя импульсов рассматривают следующую модель:

1. Пусть момент к = 0, U(k) = 0, k = 1, 2,…

U(0*T) = 1(t) – 1(t – σT)

L {U(0*T)} =

U(0*T) – ИПХ формирователя импульсов

W_фи(s) = L{ U(0*T)}

W_фи(s) =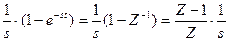

ПФ формирователя импульсов рассматривают всегда вместе с объектом, т. к. они соединены последовательно, то W_фи(s)*W₀(s) =

Для нахождения дискретной модели этого соединения:

W₀(Z) = Z{L^-1{ W_фи(s) *W₀(s)}}

Необходимо найти решетчатую функцию, соответствующую этой ИПХ:

W₀(Z) =

W₀(s)*1/s – приведенная ПФ объекта

Приведенная ПФ совпадает с переходной характеристикой объекта. Таким образом, для определения ПФ требуется:

1. определить h(t) = L^-1{W₀(s)*1/s} – ПХ объекта управления

2. t = kT, k = 0, 1, 2,… h(k) – решетчатая функция

3. найти изображение W₀(Z) = Z{h(kT)}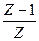

Пример определения ПФ W₀(Z): ОУ – апериодическое звено с коэффициентом усиления к₁ и постоянным временем Т₁

W₀(s) = , σ = 1

1. L^-1{W₀(s)*1/s} = k₁(1-e ^{–α t}), α₁ =

2. решетчатая функция h(k) = k₁(1-e ^{–α k T}), Т – период квантования

3. Найдем Z – изображение:

Z{h(k)} =

= k₁[(1+Z^-1+Z^-2+…)Z^-1 – e^{-α T}Z^-1(1+e^{-α T}Z^-1+e^{-2 α T}Z^-2+…)] = k₁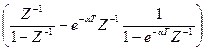

Z{h(k)} = k_1, d = e^{-α T}

W₀(Z) = 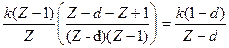- ПФ

Рассматривая ПФ, соответствующую дискретной модели, позволено рассматривать модель в 2-х видах:

Z^-1 – оператор запаздывания

Z – оператор опережения

ε(k) = ε(kT), k = 0, 1,…

y(Z) = E(Z)*W(Z)

Особенность этой системы – квантование сигнала рассогласования.

Найдем ПФ замкнутой системы:

E(Z) = V(Z) – y(Z)

y(Z) = W(Z)(V(Z) – y(Z))

W(Z) = W_дф*W₀(Z)

Ф(Z) = y(Z)/V(Z) =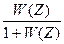

W(Z) – ПФ разомкнутой системы

Ф(Z) – ПФ замкнутой системы

(*) ε(t) = V(t) – y(t)

y(k)E(k)*W(Z)

(**) E(k) = V(k) – y(k-1)

Ф(Z) = y(Z)/V(Z) =

(*) и (**) – уравнения замыкания

Объект может описываться не только уравнениями входных – выходных(ПФ), но и уравнениями состояния.

66. Передаточная функция объекта, описанного уравнениями состояния при кусочно-постоянном уравнении.

x́(t) = Ax(t) + BU(t) – уравнение состояния объекта

y(t) = Cx(t) – уравнение выхода

U(t) = U(kT) = U_k, t[kT,(k+1)T]

Найдем дискретную модель объекта при y(k) = y(t), t = kT

Рассмотрим общее решение уравнения:

x(t) = e^A x(t₀) + B U(τ)dτ

t₀ = kT, t = (k+1)T

x(k+1) = e^ATx(k) + 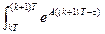B U(τ)dτ

Учтем, что

1. U(τ) =

(k+1)T-τ = σ

x(k+1) = e^AT x(k) +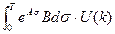

A_d = e^AT, detA

B_d =

x(k+1) = A_d x(k) + B_d U(k)

y(kT) = C x(k)

e^AT = A_d

1. e^AT = L^-1{(sI-A)^-1}

2. t = T

3. e^AT

Zx(Z) = A_d x(Z) + B_d U(Z)

y(Z) = C x(Z)

x(Z) = (ZI - A_d)^-1 B_d U(Z)

y(Z) = C (ZI - A_d)^-1 B_d U(Z)

W(Z) = 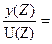C (ZI - A_d)^-1 B_d

67. Устойчивость дискретных систем.

Устойчивость определяется корнями характеристического уравнения.

1. Для модели вход – выход:

Ф(Z) =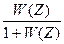

W(Z) = - ПФ разомкнутой

системы

ПФ замкнутой системы:

Ф(Z) = , где Д(Z) = D(Z) + C(Z) – характеристический многочлен замкнутой системы

Д(Z) = 0, Z_i, i = ,

Д(Z) * y(k) = 0

y(k) = , где Z_i – корни характеристического уравнения

C_i – произвольная постоянная

Если y(t) 0 при к∞, то тривиальное решение уравнения Д(Z) * y(k) = 0, y(k) = 0

называется равномерным асимптотически устойчивым. Необходимое и достаточное условие:

i = , x_св[n]→0, n→0

Для анализа устойчивости разрабатываются примерные устойчивости дискретных систем, которые аналогичны критической устойчивости непрерывной системы.

Если корни принадлежат площади этого круга, то система

устойчива; если за пределами круга, то неустойчива; если

на границе, то будут периодические колебания.

i = ,

y[k]→0, k→0, y[k]

y[k] =

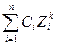
, y(k)→0, k→∞

y(k) →∞, k→∞ - система неустойчива

W(Z) =

Характеристический многочлен замкну-

той системы:

Ф(Z) = = =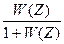

Если есть система автоматического управления (MATLAB, MathCad), то достаточно применить оператор для нахождения корней. Если выбрать W(Z, k₁, T₁),то Д(Z, k, T₁).

k₁[k_1min, k_1max], T₁[T_1min, T k_1max],

Z_i (k₁, T₁) – траектория корней характеристического уравнения i = ,

Часто для описания дискретной модели используются уравнения состояния:

x[n+1] = A_d x(k) + B_d U(k)

y(k) = C_d x(n)

x(k)Rⁿ

U(k)R^m

y(k)R^l

Исследование устойчивости такой системы связано с оценкой корней характеристического уравнения системы.

det (ZI - A_d) = 0

Раскрытие определителя при больших n сопровождается ошибкой округления (ошибки счета). Ошибки счета могут привести к тому, что корни будут существенно отличаться от истинных.

Z_i = Z_i (A_d), i = ,

Поэтому при определении устойчивости стараются избежать:

Д(Z) = det (ZI - A_d) – характеристический многочлен

Для этого используют критерии устойчивости. Среди них выделяют критерий Зубова:

A_d2 = A

А_d4 = A* Aи т.д.

Если A_d2n→0, то все корни лежат внутри единого круга, зн., система устойчива.

Если , то среди корней есть такие, которые не лежат внутри окружности, зн., и система неустойчива.

68. Анализ качества дискретных систем.

Методология анализа качества дискретных систем аналогична методологии анализа качества непрерывных систем.Анализ качества дискретных систем в 2-ч режимах:

- в установившемся режиме

- в переходных процессах

Анализ в установившихся режимах сводится к определению показателей качества переходной характеристики. Рассмотрим этот анализ более подробно:

69. Анализ ошибок воспроизведения входных сигналов.

W₁(Z) – цифровой регулятор

W₂(Z) - отраженная ПФ объекта управления

1. ошибка по входу: E(Z) = Ф_ε (Z) V(Z)

2. E_f(Z) = Ф_f(Z) F(Z)

Ф_ε (Z) = - ПФ по ошибке воспроизведения входного сигнала

Ф_f(Z) = 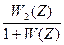- ПФ по возмущению

Е_п(Z0 = Z{e(k)} = E(Z) + E_f(Z) = Ф_ε (Z) V(Z) + Ф_f(Z) F(Z) – полная ошибка

Анализ этих ошибок производится по действию типовых сигналов.

V(k), f(k) – типовые сигналы, к = 0, 1, 2,…

В качестве типовых сигналов используют дискретные полиномиальные сигналы.

g(k) – типовой сигнал (дискретный полиномиальный сигнал порядка r)

g₀(k) = 1(k), к = 0, 1, 2,…

g₁(k) = kT, к = 0, 1, 2,…

g₂(k) = 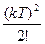, к = 0, 1, 2,…

g_r(k) = , к = 0, 1, 2,…

При r = 0 1(t) 1(k)

При r = 1, t kT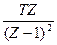

При r = 2,

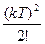
g₀(k) – статические ошибки

Е_ст(t) = Ф_ε (Z) * - изображение статической ошибки

Е_cк(Z) = Ф_ε (Z) * 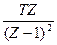- изображение скоростной ошибки

Е_уcк(Z) = Ф_ε (Z) *

Величины этих ошибок оценивают исходя из теоремы о конечных значениях:

g(nT), n = 0, 1, 2,… - решетчатая функция

Z{g(n)} = G(Z)

lim g(kT) = lim (Z-1) G(Z)

_{k→∞ k→∞}

Значения ошибок зависят от порядка астатизма дискретной системы и от порядка дискретного полинома.

υ – порядок астатизма

r – порядок дискретного полинома

Включим сумматор в цепь прямой передачи сигнала.

y(k) =

Z{y(k)} = y(0)Z⁰ + y(1)Z^-1 + y(2)Z^-2 + …= g(0)Z⁰ + (g(0) + g(1))Z^-1 + (g(0) + g(1) + g(2))Z^-2 + …=

= g(0) (1 + Z^-1 + Z^-2 + …) + g(1) Z^-1 (1 + Z^-1 + …) + g(2)Z^-2 (1 + Z^-1 + …) = G(Z)

W_∑(Z) =

W(Z) =

W₀(1) = 1

Ф_ε (Z) =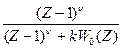

ε_ст = lim (Z)

1. υ = 0 – статическая ошибка в статической системе

ε_ст =

V(n) = a₀ 1(t)

ε_ст = a₀ / (1+k)

2. υ = 1, 2,… ε_ст = 0

r = 1

ε_сk = lim (Z→1)

a) υ = 0 ε_сk = ∞

b) υ = 1 ε_сk = ε_сk =

V[n] = a₁nT, T>0

c) υ = 2, 3,… ε_сk = 0

r = 2 V(n) =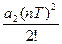

ε_усk = lim (Z→1)

υ = 0, 1 ε_усk = ∞

υ = 2 ε_усk =

Аналогичные ошибки возникают при действии полиномиального возмущения:

W₁(Z) =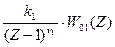

W₂(Z) =

W(Z) =

70. Типовые законы регулирования, реализующиеся цифровыми регуляторами.

1. П – закон

2. И – закон

3. ПИ – закон

4. ПИД – закон

5. ПД – закон

П – закон:

U(k) = k_p - коэффициент усиления регулятора

U(Z) = k_p E(Z)

W_п(Z) = k_p =

И – закон:

U(k) = k_и

U(Z) = k_и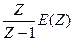

W_и(Z) = , υ = 1

ПИ – закон:

U(k) = k_р e(k) + k_и

U(Z) = (k_р + k_и

W_пи(Z) = 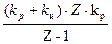, υ = 1

Быстродействие законов аналогично быстродействию непрерывных законов.

ПИД – закон:

U(k) = k_р e(k) + k_и + k_д(e(k) – e(k-1))

U(Z) = (k_р + + k_д(1-Z^-1))E(Z)

W_пид(Z) = k_р + + k_д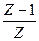

ПД – закон:

самостоятельно!

71. Анализ качества переходных процессов дискретных систем.

1. Рассмотрим дискретную модель системы:

Для анализа качества переходных процессов дискретных систем используют те же подходы, что и для непрерывных систем. Качество переходных процессов оценивается по переходной характеристике. Переходная характеристика – это реакция системы на единичный скачок при нулевых входах и нулевых начальных условиях.

1(k) = 1, k = 0, 1, 2,…

Данная структура имеет 2 входа, поэтому структура имеет 2 переходных характеристики:

1. V (k) = 1(k), f(k) = 0

Переходная характеристика по входу h(k)

2. f(k) = 1(k), V(k) = 0

h_f(k), k = 0, 1, 2,… - переходная характеристика по возмущению

σ- ПИ – регулятор

h_m = max h (k)

_k

h_уст – установившееся значение переходной характеристики

h_уст = lim (Z-1) H(Z) при Z→1

H(Z) = Z{h(k)}

Значение σ не всегда будет точно отражать ПИ – регулятор. Если же нужна более точная оценка ПИ-регулятора, то вместо обычного Z – преобразователя надо использовать смещенную или модификацию Z – преобразования. Для построения переходной характеристики можно использовать следующие функции:

1. h(k), h_f(k)

H(Z) H_f(Z)

H(Z) = Ф(Z)

H_f(Z) =

2. Формулы обращения Z - преобразований

h(k) = Z^-1{H(Z)}

H_f(Z) = Z^-1{ H_f(Z)}

Существует несколько путей вычисления формул обращения Z- преобразований:

а) теорема разложений

Пусть H(Z) =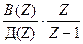

Теорема использует полюсы

Z_i = 1 Д(Z) = 0 Z₂,…,Z_n+1

h(k) =

Д́(Z_i) =

На основе разложения в ряд Лорана:

H(Z) = Ω₀ + Ω₁Z^-1 + Ω₂Z^-2 + …

H(Z) = h(0) + h(1) Z^-1 + h(2) Z^-2 + …

Ω₀ = h(0), Ω₁ = h(1), …,Ω_k = h(k), k = 0, 1, 2,…

B(Z) = β₀Z^m + β₁Z^m-1 + … + β_m

Д(Z) = α₀Zⁿ + α₁Z^n-1 + … + α_n

Особенность дискретной системы: принципиальная возможность построения системы с конечной длительностью ПП.

Если Д(Z) = Zⁿ, Zi = 0, i = , то ПП будет длиться n шагов.

B(Z) = 1

72. Пример определения ПХ.

1. ДФ представляет собой П – закон регулирования К_д; W_д(Z) = К_д

2. Формирователь в виде ЦАПа (фиксатор нулевого порядка)

W_ф(Z) =

3. Объект W₀(s) =

W₀(Z) = Z{h₀(k)}

h₀(k) – h₀(t), t = kT; ПХ непрерывного объекта

Определим ПФ W₀(Z)

h₀(t) = k₁ - = k₁ (1 – e^-αT); α =

h₀(k) = k₁(1(k) – d^-αkT)

Z{ h₀(k)} = k_{1= ,} где d = e^-αT – период квантования

Определим ПФ разомкнутой системы:

W(Z) = W_д(Z) * W_ф(Z) * W₀(Z) = k_д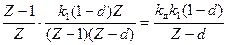

Найдем ПХ по входу:

H(Z) =

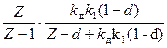
h(k) = Z^-1{H(Z)}

Если для описания динамики системы используют разностное уравнение системы, то их решение получают рекуррентным вычислением его ординат.

Литература:

1. Бесекeрский В. А., Попов Е. П. Теория систем автоматического управления.

. Изд. 4-е Санкт-Петербург. Изд. «Профессия» 2004 г.

2. Методы классической и современной теории автоматического управления в 5-ти томах под ред. Н. Д. Егупова, М. 2000г. Т. 1, т.2

3. Мирошник И. В. Теория систем автоматического управления. Линейные системы СПб. 2005

4. Теория автоматического управления под ред. А. А. Воронова. М.: 1986 г. Часть 1 (2)

5. Афанасьев, Калмановский, Носов Математическая теория конструирования систем управления, М.: 1989г.

6. Теория автоматического управления под редакцией Яковлева, М. 2003г.

7. Певзнeр Л. Д. Теория систем управления, М.: 2002 г.

8. Шишмарев В.Ю. Основы автоматического управления.- М.: «Академия», 2008 г.

9. Малафеев С.И., Малафеева А.А. Основы автоматики и систем автоматического управления: учебник для студ. ВУЗов. – М.: Издат. Центр «Академия», 2010, 384с.

10. Коновалов Б.И., Лебедев Ю.М. Теория автоматического управления: учебное пособие, 3-е изд. – СПб. Изд-во «Лань», 2010.

Дата добавления: 2014-01-15