
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перейти к пределу под знаком функции
|
|
|
|
А
А-ε а+ε х Рис.3 Поэтому определение предела последовательности геометрически можно сформулировать так: число а называется пределом последовательности {xn}, если для любойε-окрестности точки анайдется натуральное число N,что все значения xn, для которых n> N,попадут в ε-окрестности точки а. Ясно,что чем меньше ε,тем больше числоN,но в любом случае внутри ε-окрестности точки а находится бесконечное число членов последовательности,а вне ее может быть лишь конечное их число. Отсюда следует,что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела,называется расходящейся. Итак,если последовательность имеет пределом конечное число,то говорим что она сходится. Пример: N 1,3,4,7. Если последовательность не имеет предела или предел равен ∞,то говорим,что она расходится. Пример: N 2,5,6. Постоянная последовательность xn=С, n € Nимеет предел,равный числуС,т.е.limС=С.Действительно, для всех при всех натуральных nвыполняется .Имеем | хn-С |=| С-С |=0<ε. 3.3.Основные свойства сходящихся последовательностей. 1).Единственность предела TЕОРЕМА 1. Всякая сходящаяся последовательность имеет только один предел. 2).Необходимое условие сходимости последовательности. TЕОРЕМА 2. Всякая сходящаяся последовательность ограничена. Обратное утверждение неверно т.е.не всякая ограниченная последовательность сходится,например,последовательность с общим элементом (-1)n ограниченна, но расходится. 3).Сходимость монотонной последовательности. TЕОРЕМА 3. Монотонная ограниченная последовательность сходится. Следствие из Теорем 2 и 3 (Критерий сходимости монотонной последовательности): Монотонная последовательность сходится тогда и только тогда,когда она ограничена. 4).Арифметические операции над сходящимися последовательностями. Последовательности {xn+yn}, {xn-yn}, {xn*yn}, {xn/yn}, называются сумма,разность, произведение и частное последовательностей {xn}, {yn} соответственно (для частного предполагается,что yn≠0,. TЕОРЕМА 4. Если,,то I. lim(хnуn)=lim хn lim уn= а в II. lim(хn·уn)=lim хn · lim уn= а·в III. lim(хn)p = (lim хn)p, p ЄIN IV. lim== (хn≠0 и lim уn≠0, n ЄIN)в≠0 V. lim=,(p ЄIN e хn≥0, n ЄIN,если pЄ{числа парные}. 5).Предельные переходы в неравенствах. TЕОРЕМА 5. Если,,и начиная с некоторого номера выполняется неравенство xn≤yn,то а ≤ в. TЕОРЕМА 6. Если и и начиная с некоторого номера, выполняется неравенство:xn≤zn≤yn, то =a. Классификация последовательностей в зависимости от существования предела. {un} В частном случае,если a=0, последовательность {un} является бесконечно малой. ПРИМЕР. un=an, a R: a<-1; не монотонная; lim не существует → (-2)n- колеблющаяся, a=-1; не монотонная; lim не существ. → (-1)n- колеблющаяся, -1<a<0; не монотонная; lim an=0 → (-1/2)n- сходится, a=0; постоянная; lim an=0 → (0)n- сходится, 0<a<1; убывающая; lim an=0 → (1/2)n- сходится, a=1; постоянная; lim an=1 → (1)n- сходится, a>1; возрастающая; lim an=∞ → (1/2)n- расходится. 3.4.Бесконечно большие и бесконечно малые последовательности. Определение.Бесконечно большой последовательностью(б.б.п.) называется последовательность {xn},если. Обозначается:. Например: 1). 3,5,7,9,11... –неограниченная,б.б.п.,; 2). 3,1,-1,-3,-5,… - неограниченная,б.б.п.,. Замечание: б.б.п.. Определение. Бесконечно малой последовательностью(б.м.п.) называется последовательность {αn},если. Обозначается:. Например: -б.м.п.,. Замечание: б.м.п.. ТЕОРЕМА 1.(взаимосвязь между б.м.п. и б.б.п.). Если {xn} –б.б.п., xn≠0 Если {αn} –б.м.п., αn≠0 ТЕОРЕМА 2.Произведение бесконечно малой последовательности и ограниченной последовательности-бесконечно малая последовательность. §4.Предел функции. 4.1. Предел функции в точке. Пусть функция у=f(х)определена в некоторой окрестности точки а, кроме,быть может,самой точки а (эта окрестность называется проколотой окрестностью точки а,т.е. окрестность точки за исключением самой точки. . Определение (по Коши или на «языке ε-δ»).Число А называется пределом функции у=f(х)в точке а (или при х→ а) если для любого положительного εнайдется такое положительное число δ, что для всехх≠а, удовлетворяющих неравенству | х-х0|<δ выполняется неравенство | f(х)-A|<ε. Записывают lim f(х)=A. х→ а Коротко| х-а|<δ, х≠а ↔ | f(х)-A|<ε lim f(х)=A. х→ а Геометрический смысл предела функции. lim f(х)=A,если для любой ε-окрестности точки А найдется такая х→ а δ-окрестность точки а, что для всех х≠а из этой δ-окрестности соответствующие значения функции f(х) лежат в окрестности точки А. у у=f(х) А+ε
|
|
|
|
|
|
А-ε
х
а-δ а а+δ
Рис.4
Т.е.точки графика функции у=f(х) лежат внутри полосы шириной 2ε,ограниченной прямыми у=А+ε,у=А-ε. Очевидно,что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
Определение (по Гейне или на «языке последовательностей»). Число А называется пределом функции у=f(х) в точке а (или при х→ а) если для любой сходящейся к а последовательности 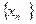 значений аргумента функции,отличных от а,соответствующая последовательность
значений аргумента функции,отличных от а,соответствующая последовательность 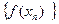 значений функции сходится к числу А ,т.е.
значений функции сходится к числу А ,т.е. 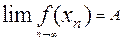 .
.
В этом случае пишут lim f(х)=A или f(х)→A при х→ а.
х→ а
Геометрический смысл предела функции.
lim f(х)=A означает,что для всех точек х, достаточно близких к точке а,
х→ а
соответствующие значения функции как угодно мало отличаются от числа А.
ПРИМЕР Доказать,что 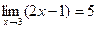
По определению: 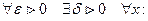 | х-а|<δ, х≠а ↔ | f(х)-A|<ε ↔
| х-а|<δ, х≠а ↔ | f(х)-A|<ε ↔
lim f(х)=A.
х→ а
Рассмотрим | f(х)-A|<ε и найдем ту окрестность точки х=3, в которой выполняется указанное неравенство. Имеем
| f(х)-A|=| (2х-1)-5|=2| х-3|<ε
Отсюда | х-3|<ε/2. Это неравенство эквивалентное 3- <х< 3+
<х< 3+
определяет окрестность точки х=3.
ПРИМЕР Доказать,что,если f(х)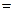 с, то
с, то 
Возьмем произвольное 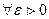 можно взять
можно взять  δ>0,тогда при | х-а|<δ, х≠а имеем | f(х)-с|= |с-с|=0 <ε. Следовательно,
δ>0,тогда при | х-а|<δ, х≠а имеем | f(х)-с|= |с-с|=0 <ε. Следовательно,  .
.
|
|
|
4.2. Односторонние пределы.
При определении предела функции 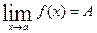 считается,что х стремится к а любым способом:оставаясь меньшим,чем а (слева), большим,чем а (справа) или колеблясь около точки а.
считается,что х стремится к а любым способом:оставаясь меньшим,чем а (слева), большим,чем а (справа) или колеблясь около точки а.
В некоторых случаях способ приближения аргумента х к а существенно влияет на значение предела функции,поэтому вводятся понятия односторонних пределов.
Определения:
Правым пределом или предел справа:
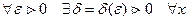 : а <х<а+δ ↔ | f(х)-A2|<ε ↔ lim f(х)=A2.
: а <х<а+δ ↔ | f(х)-A2|<ε ↔ lim f(х)=A2.
х→ а+
Левым пределом или предел слева:
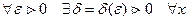 : а-δ <х<а ↔ | f(х)-A|<ε ↔ lim f(х)=A.
: а-δ <х<а ↔ | f(х)-A|<ε ↔ lim f(х)=A.
х→ а-
Коротко пределы обозначаются: Правый предел или предел справа:
lim f(х)=A2; lim f(х)=A2; f(х+0)=A2.
х→ а+0 х→ а+
Левый предел или предел слева:
lim f(х)= А1; lim f(х)=A1; f(х-0)=A1.
х→ а-0 х→ а-
Пределы функции слева и справа называются односторонними пределами.
Очевидно, если существует 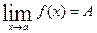 ,то существуют и оба односторонних предела,при чем А=А1=А2.
,то существуют и оба односторонних предела,при чем А=А1=А2.
Справедливо и обратное утверждение: если существуют оба предела 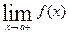 ,
, 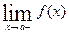 и они равны,то существует предел
и они равны,то существует предел  .
.
Если же A1 ≠A2, то 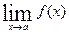 не существует.
не существует.
4.3.Предел функции при х→∞.
Пусть функция у=f(х) определена в промежутке (-∞,+∞).
Определение. Число А называется пределом функции у=f(х) при х→∞, если для любого положительного числа ε существует такое число М=М(ε)>0, что при всех х, удовлетворяющих неравенству IхI>M выполняется неравенство | f(х)-A|<ε.
Кратко можно записать:
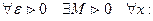 IхI>M ↔ | f(х)-A|<ε
IхI>M ↔ | f(х)-A|<ε  lim f(х)=A.
lim f(х)=A.
х→∞
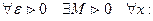 х>M ↔ | f(х)-A|<ε
х>M ↔ | f(х)-A|<ε  lim f(х)=A.
lim f(х)=A.
х→+∞
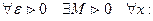 х<-M ↔ | f(х)-A|<ε
х<-M ↔ | f(х)-A|<ε  lim f(х)=A.
lim f(х)=A.
х→ - ∞
4.4.Основные свойства пределов.
Если функция у=f(х), 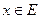 имеет предел А в точке а, то:
имеет предел А в точке а, то:
1). этот предел единственный;
2). 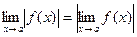 ;
;
3). 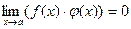 , если
, если 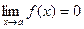 , а функция φ является ограниченной на
, а функция φ является ограниченной на
множестве Е;
4).  А±В, если
А±В, если  при
при 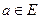 ;
;
5). 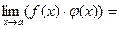
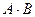 , если
, если  при
при 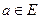 ;
;
6). 
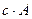 ;
;
7). 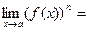
 ;
;
8). 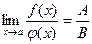 ,если
,если 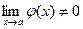 и
и  при
при 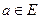 ;
;
9). 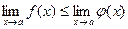 , если
, если 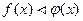 ,
, 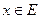 и функции f и φ имеют конечные
и функции f и φ имеют конечные
пределы в точке 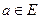 ;
;
10).если  и
и 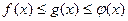 ,
,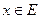 , то и
, то и 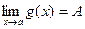 .
.
11).каждая элементарная функция f имеет конечный предел в какой-либо
точке  ,причем
,причем 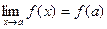 .
.
В частности, 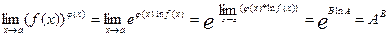 ,если
,если
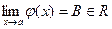 , а
, а 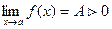 .
.
4.5.Замечательные пределы.
Первый замечательный предел и следствия из него.
|
|
|
ТЕОРЕМА. 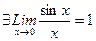 .
.
Следствия. 1).  2).
2).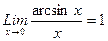 3).
3).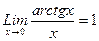 .
.
Второй замечательный предел и следствия из него.
ТЕОРЕМА.. 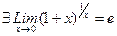
Следствия. 1). 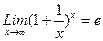 2).
2). 3).
3).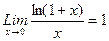
4). 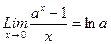 5).
5). 6).
6).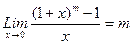 .
.
4.6.Вычисление пределов.
Преобразуемвыражение в такую форму,чтобы было легко найти предел:
ПРИМЕРЫ. 1). 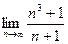 =
= (n2-n+1)=∞.
(n2-n+1)=∞.
2).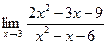 - при подстановке х=3 получаем неопределенность вида
- при подстановке х=3 получаем неопределенность вида 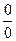 ,
,
Разложим числитель и знаменатель на множители по формуле
ах²+вх+с=а(х-х )(х-х
)(х-х ), где х
), где х ,х
,х - корни квадратного трехчлена ах²+вх+с:
- корни квадратного трехчлена ах²+вх+с:
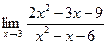 =
=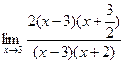 =
=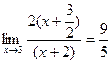
3). 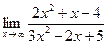 - неопределенность вида
- неопределенность вида 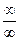 .
.
Вынесем за скобки дроби старшей степени переменной в числителе и знаменателе: 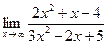 =
= .
.
4). 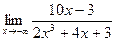 - неопределенность вида
- неопределенность вида 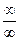 .
.
Раскрываем ее аналогично тому как это сделано в примере 3.
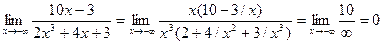 .
.
5).  -неопределенность вида
-неопределенность вида 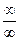 .
.
Раскрываем ее аналогично тому как это сделано в примере 3.
6).Найти предел функции 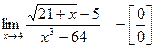 .
.
Умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель ( ), который при
), который при  не равен нулю. В результате неопределенность будет раскрыта или когда имеем иррациональные выражения уместно умножать и числитель и знаменатель на это выражение,но со знаком противоположным:
не равен нулю. В результате неопределенность будет раскрыта или когда имеем иррациональные выражения уместно умножать и числитель и знаменатель на это выражение,но со знаком противоположным:
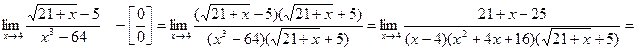
 .
.
7).Найти предел функции 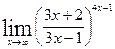 -неопределенность вида
-неопределенность вида 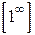 . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом  .
.
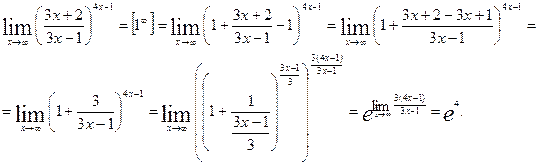
8). Найти предел функции 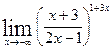 .
.
В данном примере при выяснении вида неопределенности видим, что таковой не имеется. Имеем  , тогда
, тогда
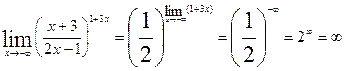 .
.
9).Найти предел, используя эквивалентные бесконечно малые функции
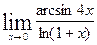 - неопределенность вида
- неопределенность вида 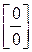 .
.
Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как
 и
и  , то
, то
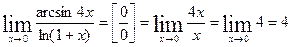 .
.
§5.Бесконечно большая функция и бесконечно малая функция.
Определение1. Функция f(х) называется бесконечно малой в точке а (б.м.ф.), если
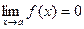 .
.
Определение2. Функция f(х) называется бесконечно большой в точке а (б.б.ф.), если для любой последовательности 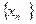 значений аргумента,
значений аргумента, 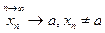 ,соответствующая последовательность значений функции
,соответствующая последовательность значений функции 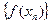 является бесконечно большой последовательностью. Обозначается
является бесконечно большой последовательностью. Обозначается 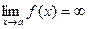 .
.
Если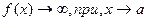 и принимает лишь положительные значения,то
и принимает лишь положительные значения,то  ,
,
если лишь отрицательные значения,то 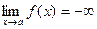 .
.
ПРИМЕРЫ: 1). 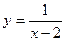 есть б.б.ф. при х→2
есть б.б.ф. при х→2
2).y=2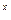 есть б.б.ф. при х→∞
есть б.б.ф. при х→∞
3).y=x² есть б.м.ф. при х→0
4). y=x-2 есть б.м.ф. при х→2
5) y=sinx есть б.м.ф. при х→πκ,  .
.
Замечание1. На бесконечно малые и б. большие функции можно перенести все свойства,которые были у бесконечно малых и б.больших последовательностей.
1). 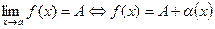 ,
, 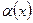 - б.м.ф.
- б.м.ф.
2).Сумма,разность и произведение конечного числа б.м.ф. - б.м.ф.
3). Связь между б.м.ф. и б.б.ф. Обратная к б.м.ф. - б.б.ф.; обратная к б.б.ф. - б.м.ф. ( Если 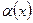 - б.м.ф., то
- б.м.ф., то 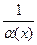 - б.б.ф. и наоборот).
- б.б.ф. и наоборот).
5.1. Сравнение бесконечно малых функций.
Сумма,разность,произведение двух б.м.ф. есть функция бесконечно малая.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть  - б.м.ф. при х→а, т.е.
- б.м.ф. при х→а, т.е. 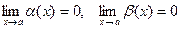 .
.
1. Если 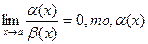 - бесконечно малая более высокого порядка,чем
- бесконечно малая более высокого порядка,чем 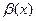 .
.
2. Если  - бесконечно малые одного порядка.
- бесконечно малые одного порядка.
3. Если 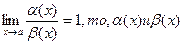 - эквивалентные бесконечно малые(при х→а).
- эквивалентные бесконечно малые(при х→а).
Обозначается:  ~
~
4. Если  - несравнимые бесконечно малые.
- несравнимые бесконечно малые.
Замечание .Аналогичные правила сравнения б.м.ф.и при 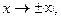
 .
.
ПРИМЕРЫ: 1). 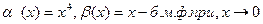 , т.к.
, т.к.
 =
= ,то
,то  -бесконечно малая более высокого порядка, чем
-бесконечно малая более высокого порядка, чем 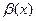 , Это обозначает,что
, Это обозначает,что стремится к 0 быстрее,чем
стремится к 0 быстрее,чем 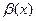 .
.
2). 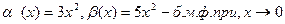 ,т.к.
,т.к.
 =
=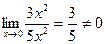 ,то
,то  и
и 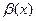 -бесконечно малые одного порядка.
-бесконечно малые одного порядка.
Это обозначает,что и
и 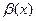 стремятся к нулю с примерно одинаковой скоростью.
стремятся к нулю с примерно одинаковой скоростью.
3). 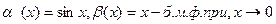 , т.к.
, т.к.
 =
=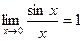 ,то
,то 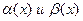 -эквивалентные б.м.ф.
-эквивалентные б.м.ф.
4). Можно ли сравнить ф-ции 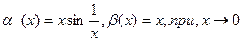 ?
?
 =
=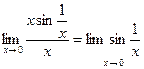 - не существует,несравнимые бесконечно малые.
- не существует,несравнимые бесконечно малые.
5.2.Эквивалентные бесконечно малые функции.
ТЕОРЕМА. (ПРИНЦИП ЗАМЕНЫ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ НА ЭКВИВАЛЕНТНЫЕ)
Предел отношения двух б.м.ф. не изменится,если каждую или одну из них
заменить эквивалентной ей бесконечно малой.
Если  ~
~  ,
, 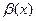 ~
~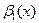 при x→а и,
при x→а и,  и эти
и эти
пределы равны.
Следствие. При вычислении пределов при x→0 можно заменять б.м.ф.
на более простые, эквивалентные им, только в произведении и в частном.
ВАЖНЕЙШИЕ ЭКВИВАЛЕНТНОСТИ,
КОТОРЫЕ ИСПОЛЬЗУЮТСЯ ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛОВ.
1). sin x ~ x при x→0; 6). 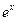 - 1 ~ x при x→0
- 1 ~ x при x→0
2). tg x ~ x при x→0; 7). 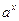 - 1 ~ x *ln a при x→0;
- 1 ~ x *ln a при x→0;
3). arcsin x ~ x при x→0; 8). ln (1+x) ~ x при x→0;
4). arctg x ~ x при x→0; 9). loga (1+x) ~ x* loga e при x→0
5). 1-cos x ~ x ²/2 при x→0; 10). - 1 ~ k * x, к>0 при x→0;
- 1 ~ k * x, к>0 при x→0;
например, √ (1+ x) – 1 ~ x /2
Геометрическая интерпретация эквивалентности б.м.ф.
Графики эквивалентных функций в окрестности точки 0 практически не различимы,т.е. sin x ≈ x при x→0 и т.д.
ПРИМЕР: Найти предел 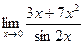
Поскольку 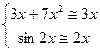 при x→0
при x→0 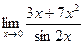 =
=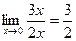 .
.
§6. Непрерывность функций.
Определение. Функция f (х) называется непрерывной в точке а, если:
1).эта функция определена точке а и в некоторой окрестности этой точки;
2).существует конечный предел 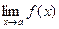 ;
;
3).этот предел равен значению функции в этой точке, т.е. 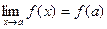 . (1)
. (1)
Полагая х= а +∆ а, где ∆ а →0, можно переписать условие (1) так:
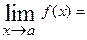
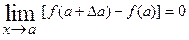 ,
,
т.е. функция f (х) непрерывна в точке а тогда и только тогда,когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Определение. Если функция непрерывна в каждой точке некоторой области (интервала,сегмента и т.п.),то она называется непрерывной в этой области.
Определение. Если функция непрерывна в интервале (а,b) и в точке х=а непрерывна
справа(т.е. 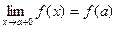 ) и в точке х=b непрерывна слева(т.е.
) и в точке х=b непрерывна слева(т.е.  ) ,то
) ,то
она называется непрерывной на отрезке [а,b].
Следствие. Так как 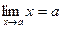 , то условие (1) можно записать в виде:
, то условие (1) можно записать в виде:
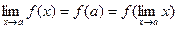 .
.
Это значит, что при нахождении предела непрерывной функции можно
Например, 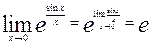 .
.
6.1.Точки разрыва функции и их классификация.
Определение. Точки,в которых нарушается непрерывность функции,называются
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 749; Нарушение авторских прав?; Мы поможем в написании вашей работы!