
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Знакочередующиеся ряды.Признак Лейбница
|
|
|
|
Знакочередующиеся и знакопеременные ряды.

 Рассмотрим важный класс рядов, называемый знакочередующимися.
Рассмотрим важный класс рядов, называемый знакочередующимися.
Определение. Знакочередующимся рядом называется ряд вида

 u1 – u2 + u3 - u4 +…+(-1)
u1 – u2 + u3 - u4 +…+(-1) un +...,
un +...,
где u1,u2,u3...,- положительные для всех n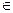 N.
N.

ТЕОРЕМА (ПРИЗНАК ЛЕЙБНИЦА). Знакочередующийся ряд
u1 – u2 + u3 - u4 +… (un>0), (4.1)
сходится,если последовательность абсолютных величин членов ряда монотонно убывает,т.е. u1>u2>u3>… (4.2)
и если  un=0 (4.3)
un=0 (4.3)
при этом сумма S ряда(4.1) удовлетворяет неравенствам 0<S <u1.
Для остатка ряда  в этом случае справедлива оценка
в этом случае справедлива оценка  .
.
ПРИМЕР. Исследовать сходимость ряда:

Имеем:1>1/4>1/9>...– члены ряда монотонно убывают и 
 =0.
=0.
По Теореме Лейбница ряд сходится.
Замечание: В Т.Лейбница важны как условие  un=0, так и u1>u2>u3>...
un=0, так и u1>u2>u3>...
Например,для ряда 
 un=0,но условие
un=0,но условие
1/ 0,41>1/2,41 >1/1,73 >1/2,73... или
2,44>0,41>0,58>0,37... неверно и ряд расходится.
ПРИМЕР. Вычислить приблизительно сумму ряда  .
.
Имеем знакочередующийся ряд,сходится.Возьмем пять элементов этого ряда:
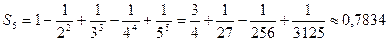 ,
,
Вычислим ошибку: 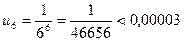 ; итак,
; итак,  .
.
4.2.Абсолютная и условная сходимость знакопеременных рядов.
Определение. Знакочередующийся ряд является частным случаем знакопеременного ряда.Числовой ряд,содержащий бесконечное множество положительных и бесконечное множество отрицательных элементов,называется знакопеременным.
 TEOРEMA(общий достаточный признак сходимости).
TEOРEMA(общий достаточный признак сходимости).
Пусть дан знакопеременный ряд
 u1 + u2 + … + un +… (4.4)
u1 + u2 + … + un +… (4.4)
если сходится ряд
 (4.5)
(4.5)
составленный из модулей элементов данного ряда,то сходится и сам знакопеременный ряд.
ПРИМЕР: Исследовать на сходимость  (4.6)
(4.6)
где α какое -либо число.
Рассмотрим (4.7)
(4.7)
и 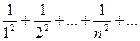 (4.8)
(4.8)
ряд (4.8) сходится, потому что α=2>1;
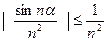 , по 1 признаку сравнения
, по 1 признаку сравнения
|
|
|
ряд (4.7) также сходится.По Теореме рассмотренной ряд (4.6) сходится тоже.
Признак сходимости рассмотренный является достаточным,но не
необходимым, существуют знакопеременные ряды, которые сходятся,но чьи ряды абсолютных величин расходятся..
Поэтому введем понятия абсолютной и условной сходимости.
Определение. Знакопеременный ряд
u1 + u2 + … + un + (4.9)
называется абсолютно сходящимся,если ряд,составленный из модулей его элементов, сходится: Iu1I +Iu2I + … +IunI… (4.10)

Если ряд (4.9) сходится, но ряд (4.10) расходится, ряд (4.9) называется условно сходящимся.

ПРИМЕР. Знакочередующийся ряд
 - условно сходится, (4.11)
- условно сходится, (4.11)
поскольку ряд величин абсолютных - это ряд гармонический
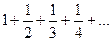 который расходится и (4.12)
который расходится и (4.12)
ряд (4.11) сходится по Пр.Лейбница(как знакочередующийся ряд):
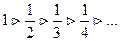 И
И  .
.
ПРИМЕР. Ряд 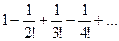 абсолютно сходится,
абсолютно сходится,
поскольку ряд величин абсолютных
 сходится по Пр.Даламбера:
сходится по Пр.Даламбера:
 .
.
ПРИМЕР. 2 - 3/2 + 4/3 - 5/4 +... (-1)n+1(n+1) / n+...
ряд знакочередующийся, по Пр.Лейбница:
2>1,5>1,3>... и l - условия неверны, ряд расходится.
- условия неверны, ряд расходится.
Свойства абсолютно сходящегося ряда.
1).Если ряд ∑ un сходится абсолютно,то любой ряд,полученный из данного перестановкой элементов,также сходится абсолютно и имеет ту же сумму. Условно сходящиеся ряды таким свойством не обладают.
2).Абсолютно сходящиеся ряды с суммами S1,S2 можно почленно складывать(вычитать).В результате получается абсолютно сходящийся ряд,сумма которого равна S1+S2 (или S1-S2).
3).Если ряд u1+u2+u3+… и v1+v2+v3+… сходятся абсолютно и если
S1,S2 –суммы их,ряд u1v1+(u1v2+v1u2)+(u1v3+u2v2+u3v1)+…+(u1vn+u2vn-1+unv1)+… сходится абсолютно. Этот ряд называется произведением рядов (по Коши).Сумма его равна S1S2.
Свойства условно сходящегося ряда.
ТЕОРЕМА РИМАНА. Если ряд ∑ un условно сходится, то для любого наперед
заданного числа L можно так переставить элементы этого ряда,что получится ряд,
имеющий сумму L (и даже можно получить расходящийся ряд).
Поэтому действия над рядами необходимо производить,убедившись в их
|
|
|
абсолютной сходимости.Для этого используются все признаки сходимости
знакоположительных рядов,заменяя общий элемент ряда его модулем.
ПРИМЕР. Исследовать на абсолютную сходимость ряд:
½- 1/(2*22)+1/(3*23)-...(-1)n+1/(n*2n)+...
Э то знакочередующийся ряд,используем Пр.Лейбница:
1/2>1/8>1/24>... и lim [1/(n*2n)]=0 условия выполнены,ряд сходится
n→∞
Исследуем ряд с положительными элементами an=1/(n*2n)
По признаку Даламбера:  - ряд сходится.
- ряд сходится.
Итак,∑an сходится,∑IanI тоже сходится, ряд данный сходится абсолютно.
ПРИМЕР. 
Этот ряд знакочередующийся, по Пр.Лейбница:
1>0,7>0,6>... и 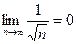 -условия верны, ряд сходится.
-условия верны, ряд сходится.
Исследуем ряд с положительными элементами:
имеем гармонический ряд с α= 1/2< 1,который расходится.
Итак,∑an cходится,∑IanI расходится, ряд условно сходящийся.
Глава 10.СТЕПЕННЫЕ РЯДЫ.
§1.Основные понятия.
Определение. Ряд,элементами которого являются функции от x называется функциональным:
f1(x) + f2(x) + f3(x) +…+ fn(x) +… (1.1)
Придавая x различные значения,получаем различные числовые ряды,
которые могут быть как сходящимися,так и расходящимися.
Определение. Областью сходимостифункционального ряда называется совокупность числовых значений аргумента x,при которых функциональный ряд сходится.
В области сходимости функционального ряда его сумма является некоторой функцией от x: S= S(x). Определяется она в области сходимости равенством
S(x)=  Sn(x), гдe
Sn(x), гдe
S (x)= f1(x) + f2(x) + f3(x) +…+ fn(x) -частичная сумма ряда.
(x)= f1(x) + f2(x) + f3(x) +…+ fn(x) -частичная сумма ряда. 
 Rn(x) = S(x) - Sn(x) -остаток. ряда.
Rn(x) = S(x) - Sn(x) -остаток. ряда.
Среди функциональных рядов особую роль играет ряд,элементами которого являются степенные функции.
Определение. Степенным рядом называется ряд вида
а +а
+а (х-х
(х-х )+а
)+а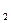 (х-х
(х-х )² +…+а
)² +…+а (х-х
(х-х )
) +…=
+…= (1.2)
(1.2)
Числа а ,а
,а ,… - коэффициенты ряда.
,… - коэффициенты ряда.
Частный случай,когда имеем ряд вида 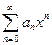 . (1.3)
. (1.3)
Степенной ряд общего вида (1.2) сводится к ряду (1.3) заменой
х-х =у, поэтому рассматриваем ряд вида
=у, поэтому рассматриваем ряд вида 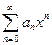 как более удобный для изучения.
как более удобный для изучения.
§2. Интервал и радиус сходимости степенного ряда.
ТЕОРЕМА АБЕЛЯ. Если степенной ряд (1.3) сходится при  , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 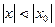 .
.
Следствие. Если ряд (1.3) расходится при 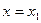 , то он расходится и при всех х, удовлетворяющих неравенству
, то он расходится и при всех х, удовлетворяющих неравенству  .
.
|
|
|
Итак,если 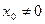 есть точка сходимости степенного ряда,то интервал
есть точка сходимости степенного ряда,то интервал 
состоит из точек сходимости данного ряда;вне этого интервала ряд (10.3) расходится.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1468; Нарушение авторских прав?; Мы поможем в написании вашей работы!