Граница области D

X

X

Y

X

Рис.2

b_k=0,

a₀= ;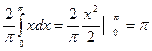

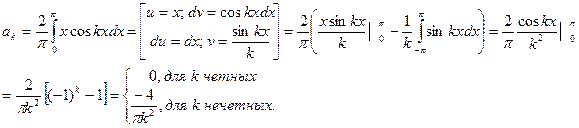
Получаем ряд: f(x)=+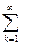(a_kcoskx + b_ksenkx)

.

2.3.Ряд Фурье для функции с периодом 2ℓ.

Пусть f(x) определена на отрезке [- ℓ, ℓ ],имеет период 2ℓ, отличающийся от 2π

(где ℓ- произвольное положительное число) и удовлетворяет на этом отрезке условиям

Дирихле. Разложим ее в ряд Фурье. Сделаем замену переменной по формуле:

.

Функция определена на отрезке [- π,π ]и имеет период 2π.

Разложение ее в ряд Фурье имеет вид:

, (2.1)

где a₀= ; ; 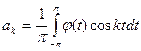(k=0,1,2...).

Возвратимся теперь к старой переменной x:

; ;

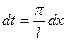
Тогда имеем: a₀= ; ; 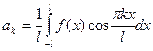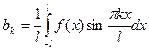. (2.2)

Формула (2.1) получит вид ( ряд Фурье для периодической функции с периодом 2ℓ):

,

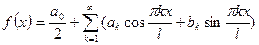где коэффициенты a₀,a_k,b_k вычисляются по формулам (2.2).

Теоремы,которые имели место для рядов Фурье 2π -периодических функций

,остаются в силе и для рядов Фурье функций с периодом 2ℓ.

ПРИМЕР. Разложить в ряд Фурье функцию периодическую с периодом 2ℓ, определенную

на отрезке [-ℓ,ℓ]:

f(x) = I x I.

Вычислимкоэффициенты Фурье,учитывая,что функция четная.

Рис.3

Для четной функции: b_k=0, ,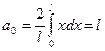

Таким образом .

2.4.Ряд Фурье для непериодических функций.

Пусть у=f(х) – непериодическая функция,заданная на всей числовой оси.

Такая функция не может быть разложена в ряд Фурье,однако непериодическая функция

f(х) может быть представлена в виде ряда Фурье на любом конечном промежутке [а,b],

на котором она удовлетворяет условию Дирихле. Для этого можно поместить начало

координат в середину отрезка [а,b] и построить функцию 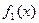периода Т=2l= 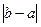такую,

что при 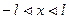(Рис. 4).

У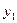

y=f(x)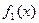

-l l

О а 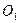b X

Рис.4.

Разлагаем функцию 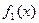в ряд Фурье.Сумма этого ряда во всех точках отрезка

[а,b] (кроме точек разрыва)совпадает с функцией f(х),вне этого промежутка сумма ряда и

f(х) являются совершенно различными функциями.

Пусть теперь непериодическую функцию f(х) требуется разложить в ряд Фурье

на отрезке [0,ℓ] (это частный случай: начало координат перенесено в точку х=а отрезка [а,b] ).

Функцию можно доопределить произвольным образом на отрезке [-ℓ,0] и продолжить

ее с периодом Т=2l.

В частности,если доопределить функцию на отрезке [-ℓ,0]четным образом

(т.е. f(х)= f(-х)),то функцияf(х) разлагается в ряд Фурье,который содержит только

косинусы (Рис.5).

Если же продолжить функцию f(x) на отрезок [-ℓ,0]нечетным образом,

то функцияf(х) разлагается в ряд Фурье,который содержит только синусы (Рис.6).

Ряд косинусов и ряд синусов для функции f(x),заданной на отрезке [0,ℓ], имеют одну и ту же сумму.

y y

^{-ℓ0 ℓ} x ^{-ℓ0 ℓ} x

Рис.5 Рис.6

ПРИМЕР. Пусть надо разложить f(x) на отрезке [0,π]

в ряд синусов f(x)=x, 0<x≤π.

Функция удовлетворяет на (0,π) условиям Дирихле. Продолжая эту функцию

нечетным образом,получим:

y

^{-3π -π π 3π}

^{-4π -2π 0 2π 4π} x

Рис.7

.

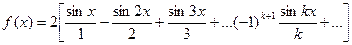ПРИМЕР разложить 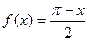на отрезке [-π,0] в ряд косинусов.

Функция удовлетворяет на (0,π) условиям Дирихле. Продолжая эту функцию

четным образом,получим:

у

Рис.8

Итак: b_k=0; ;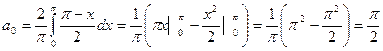

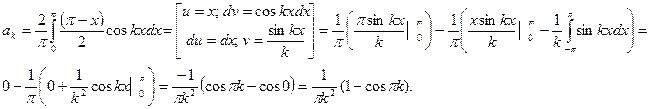
Глава 13.КРАТНЫЕ ИНТЕГРАЛЫ.

§1.Двойной интеграл.

Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

у

Di

D

О x

Рис.1

Пусть в замкнутой области D плоскости OXY задана непрерывная функция z= f(x,y). Разобьем область D на n «элементарных областей» Di (i=1,2…n) площади которых обозначим через ∆s₁, ∆s₂, ∆s₃,… ∆s_{n ,}

а диаметры (наибольшее расстояние между точками области) – через di. В каждой области Di выберем произвольную точку Р_i,получим n точек P₁ , P₂ , P₃ , …, P_n.

f(P₁), f(P₂), f(P₃),… f(P_n) - значение функции в этих точках, составим сумму произведенийf(P_i)·∆s_i:

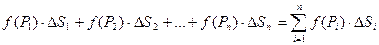
называемой интегральной суммой функции f(x,y) в области D.

Рассмотрим предел интегральной суммы,когда n_k→∞ таким образом,что

тах di →0.

Определение. Если существует предел множества сумм произведений f(P_i)*∆s_i,

при наибольшем диаметре областей элементарных ∆s _i стремящихся к нулю (тах di →0)

и при n →∞ и не зависит отспособа разбиения области D на части,ни от выбора точек

в них,то говорим,что f(x,y) является интегрируемой в области D и предел ее

называется двойным интегралом функции f(х,у) в области D и обозначается

или .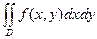

Таким образом,двойной интеграл определяется равенством

. (1.1)

ТЕОРЕМА (достаточное условие интегрируемости функции). Если функция z=f(x,y)

непрерывна в замкнутой области D,то она интегрируема в этой области.

Замечания: 1).Далее будем рассматривать только функции, непрерывные в области интегрирования,хотя двойной интеграл может существовать не только для непрерывных функций.

2).Из определения двойного интеграла следует,что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области.Таким образом,мы можем разбивать область на площадки прямыми,параллельными координатным осям.При этом ∆s_i =∆х_i* ∆y_i, равенство (1.1) можно записать в виде: .

Геометрический смысл двойного интеграла. Если функция f(x,y)≥0,то двойной интеграл f(x,y) в области D равен обьему Q тела, ограниченного сверху поверхностью z=f(x,y), снизу – замкнутой областью D плоскости Оху и,сбоков – цилиндрической поверхностью,образующая которой параллельна оси OZ,а направляющей служит

Дата добавления: 2014-01-15