Частотные характеристики импульсных систем

Частотные характеристики импульсных систем определяются аналогично обыкновенным линейным системам.

Выражения для частотных характеристик импульсных систем получаются из их передаточных функций путем замены оператора z на e^jwT. Так как частота w входит в показатель степени числа e, то частотные характеристики являются периодическими функциями частоты, период изменения которых равен ±p/T. Следовательно, нельзя различить составляющие, частоты которых кратны частоте квантования импульсного элемента w₀ = 2p/Т.

Таким образом, частотная передаточная функция разомкнутой импульсной системы имеет вид:

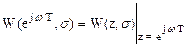. (1.77)

Функция W(e^jwT,s) представляет собой комплексный спектр дискретной передаточной функции разомкнутой импульсной системы W(z,s) и полностью характеризует частотные свойства разомкнутой системы, т.е. позволяет вычислить установившуюся реакцию системы на решетчатое гармоническое воздействие g[nT] = g_m sin[wnT] произвольной частоты w.

Как и для обыкновенных линейных систем, рассматривают амплитудную, фазовую, вещественную и мнимую частотную характеристики:

A(w,s) = mod W(e^jwT,s);

y(w,s) = arg W(e^jwT,s);

U(w,s) = Re W(e^jwT,s);

V(w,s) = Im W(e^jwT,s).

Свойства частотных характеристик импульсных систем [13].

1. Кроме зависимости от частоты w характеристики зависят от относительного времени s. Графически это выражается серией кривых для различных значений s. Обычно достаточно одной характеристики при s = 0.

2. В соответствии с периодичностью частотной передаточной функции амплитудно-фазовая частотная характеристика W(e^jwT) полностью определяется своими значениями в интервале -p¤ Т £ w £ p¤ Т.

3. Так как вещественная частотная характеристика является четной функцией, а мнимая - нечетной, то достаточно рассматривать интервал частот 0 £ w £ p¤ Т.

4. В крайних точках интервала 0 £ w £ p¤ Т амплитудно-фазовая частотная характеристика принимает вещественные значения.

5. При уменьшении периода дискретности T, т.е. при увеличении частоты квантования w₀ = 2p/Т, частотные характеристики импульсных систем приближаются к частотным характеристикам непрерывных систем. При этом частотный интервал 0 £ w £ p¤ Т растягивается на всю ось w при T ® 0.

Амплитудно-фазовая частотная характеристика разомкнутой импульсной системы W(e^jwT) строится по точкам в интервале частот 0 £ w £ p¤ Т.

Частотные характеристики импульсных систем, как следует из (1.77), описываются трансцендентными выражениями. Их определение связано со сложными расчетами, поэтому на практике применяются частотные характеристики относительно абсолютной псевдочастоты l. Переход к псевдочастоте основан на переходе от z-преобразования к w -преобразованию с помощью подстановки

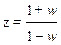(1.78)

c последующей заменой комплексной переменной w на абсолютную псевдочастоту

w = jlT/2. (1.79)

При этом реальная частота w и псевдочастота l связаны соотношением

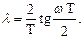(1.80)

Удобство псевдочастоты заключается в том, что, как следует из (1.80), на частотах где выполняется условие wT < 2, она приближенно равна угловой частоте, т.е. l» w. Нетрудно убедиться, что при изменении частоты от -p¤ Т до +p¤ Т псевдочастота принимает значение -¥ до +¥.

Для перехода от дискретной передаточной функции разомкнутой импульсной системы W(z) к частотной характеристике W(jl) следует сделать замену

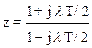, (1.81)

то есть

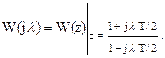(1.82)

Полученное уравнение может быть использовано для построения логарифмических частотных характеристик.

Приближенный способ построения ЛЧХ импульсных систем [2]. Для удобства логарифмические частотные характеристики строятся отдельно для областей низких и высоких частот. Границей, разделяющей частотную область на низкочастотную и высокочастотную, служит частота среза w_с в предположении, что

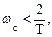(1.83)

где Т - период дискретности.

Последнее условие необходимо выполнять вследствие требований, предъявляемых к обеспечению запаса устойчивости и точности работы системы, и согласуется с теоремой Котельникова-Шеннона.

Рассмотрим методику построения ЛЧХ на примере АИС, включающей в себя экстраполятор нулевого порядка и непрерывную часть с передаточной функцией:

. (1.84)

При построении вводят следующие предположения.

1. Величина, обратная периоду дискретности T, больше половины частоты среза w_с, т.е. w_с < 2/T.

2. Переход оси нуля децибел асимптотической ЛАХ непрерывной части происходит при отрицательном наклоне -20 дб/дек.

3. Постоянным времени t_j (j = 1, 2,..., m) соответствуют сопрягающие частоты меньшие, чем частота среза.

4. Имеется l (l < n) постоянных времени T_i (i = 1, 2,..., l), которым соответствуют сопрягающие частоты меньшие, чем частота среза.

При принятых допущениях для области низких частот передаточную функцию непрерывной части можно представить в виде

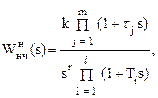(1.85)

а для области высоких частот

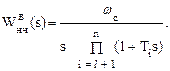(1.86)

По выражениям (1.85) и (1.86) на основании (1.64) и (1.82) получим частотные характеристики разомкнутой импульсной системы для области низких частот

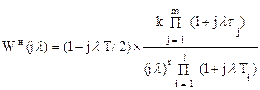(1.87)

и для области высоких частот

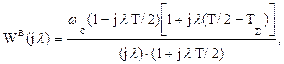(1.88)

где =.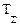

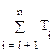Сравнение выражения (1.87) с (1.85) показывает, что в низкочастотной области частотная передаточная функция импульсной системы может быть получена из передаточной функции непрерывной части подстановкой s = jl и умножением на дополнительный множитель (1 - jlT/2). Псевдочастота l в этой области практически совпадает с угловой частотой w. Влиянием дополнительного множителя при построении частотных характеристик в низкочастотной области можно пренебречь, так как w_с < 2/T.

Таким образом, в области низких частот частотные характеристики импульсной системы совпадают с частотными характеристиками ее непрерывной части.

Начало логарифмических частотных характеристик в высокочастотной области (1.88) сливается с концом частотных характеристик, построенных в низкочастотной области. На основании (1.87) и (1.88) можно записать выражение результирующей частотной передаточной функции разомкнутой АИС

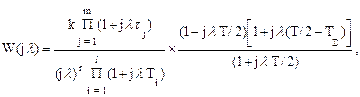(1.89)

где =.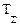

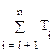Это выражение представляет собой произведение элементарных типовых сомножителей, поэтому его легко использовать для построения логарифмических частотных характеристик импульсных систем. Результирующий фазовый сдвиг определяется как

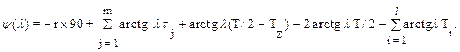
Пример. Построить логарифмические частотные характеристики АИС с экстраполятором нулевого порядка и периодом дискретности импульсного элемента T = 4 с, передаточная функция непрерывной части которой

.

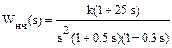Р е ш е н и е. Выбираем частоту среза w_c < 2/T < 0.5 c^-1. В соответствии с заданными постоянными времени определяем сопрягающие частоты:

w_cопр1=1/25=0.04 c^-1 - низкочастотный диапазон;

w_cопр2=1/0.5=2 c^-1 - высокочастотный диапазон;

w_cопр3=1/0.3=3.33 c^-1 - высокочастотный диапазон.

Следовательно, получаем:

,

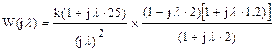где T_å = Т₁+Т₂=0.8;

,

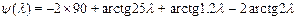l_сопр1=1/25=0.04;

l_сопр2=1/2=0.5;

l_сопр3=1/1.2=0.8.

Асимптотические ЛАХ и ЛФХ, соответствующие полученным выражениям, представлены на рис. 1.12.

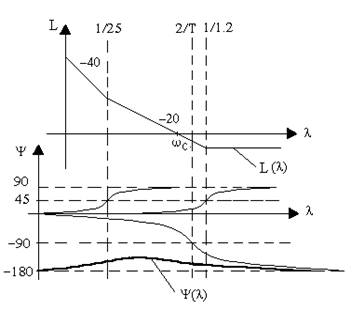
Рис. 1.12. ЛЧХ импульсной системы

Дата добавления: 2014-01-15