Границы применимости закона Дарси

Нелинейные законы фильтрации.

Установлены две основные группы причин отклонения от закона Дарси, т.е. отклонения от пропорциональной зависимости скорости фильтрации от градиента давления:

а) отклонения, связанные с проявлениями инерционных сил при высоких скоростях фильтрации (верхняя граница применимости закона Дарси);

б) отклонения при малых скоростях фильтрации, вызванные проявлением неньютоновских (реологических) свойств жидкости за счет взаимодействия ее с твердым скелетом пористой среды (нижняя граница применимости закона).

Верхнюю границу применимости закона Дарси связывают обычно с некоторым (критическим) значением чисел Рейнольдса - Re:

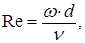
где: w- скорость фильтрации; d - некоторый характерный размер пористой среды; n - коэффициент кинематической вязкости .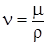

Из-за сложной зависимости чисел Рейнольдса от параметров пористой среды, существует несколько формул зависимости отмеченного типа, отличающихся различным выражением (трактованием) параметра d.

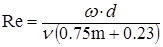– формула Павловского,

где: d_эф – эффективный диаметр зерен породы; m – пористость;

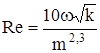– формула В.Н. Щелкачева;

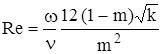– формула А.И. Абдулгавабова.

Подсчитываемые по этим формулам критические значения чисел Рейнольдса различны. Так, для зависимости Павловского Re кр. находится в пределах 7,5<Re кр.<9.

В целом, если обобщить оценки по всем формулам, то диапазон Re кр. находится в пределах 0,032<Re кр.<14. Если вычисленное значение Re меньше левого граничного значения, то фильтрация подчиняется линейному закону Дарси. Если оно больше правого граничного значения – не подчиняется; если попадает в диапазон критических значений, то имеет место неопределенность.

Для расчета критических чисел Рейнольдса, подсчитанных по приведенным формулам, В.Н. Щелкачевым предложено использовать безразмерный параметр, названный параметром Дарси.

,

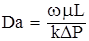где: 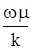- сила вязкого трения; 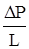- градиент давления.

Параметр Дарси представляет собой отношение силы вязкого трения и силы давления и является индикатором линейности уравнения Дарси.

Если фильтрация осуществляется в соответствии с законом Дарси (потеря давления в пласте обусловлена вязким трением и пропорциональна скорости), то безразмерный параметр Dа=1 и это равенство должно сохраняться, пока Re £ Re кр.

Введение параметра Dа упрощает исследование границы применимости закона фильтрации, если по оси абсцисс отложить lg Re (рассчитанный по одной из формул), а по оси ординат lg Da, то отклонение точек от нулевой линии укажет на наличие границы применимости закона Дарси (поскольку lg Da=0 для Re£Re кр.).

Пример зависимостей, полученных в результате обработки опытов Абдулгавабовым по формуле Щелкачева, приведен на рис. 6.4. Зависимости 1-7 получают путем увеличения скоростей фильтрации w в условиях эксперимента.

Итак, если Re >Re кр. линейный закон Дарси нарушается, он становится двучленным. Первое обобщение закона на этот случай дано Дюпюи:

,

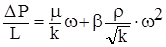где: 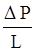- общая потеря давления; 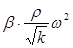- инерционная сила, связанная с кривизной поровых каналов; 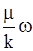- потеря давления на вязкое трение.

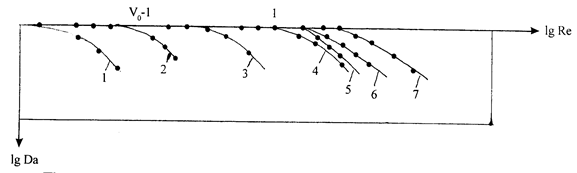
Рис. 6.4

При малых скоростях фильтрации значениями w² можно пренебречь и закон становится линейным.

Последующими работами Е.М. Минского и др. ученых показано, что эта эмпирическая формула хорошо выполняется для разных диапазонов w и имеет наибольшее физическое обоснование: потеря давления в пласте при фильтрационном течении жидкости связана с преодолением сил вязкого трения и инерционных сил гидравлического сопротивления.

Следует сказать, что при исследовании фильтрационных процессов в условиях нарушения закона Дарси используют и одночленную, но нелинейную степенную зависимость:

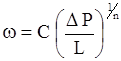, 1 < n £ 2;

б) Отклонения от закона Дарси при малых скоростях фильтрации имеет другое физическое обоснование. При малых скоростях фильтрации сила вязкого взаимодействия ~ 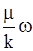пренебрежимо мала, но при этом возникает межфазовое взаимодействие между твердым скелетом и флюидом, которое не зависит от скорости, а определяется свойствами контактирующих фаз (неньютоновские силы взаимодействия).

Так нефть, содержащая поверхностно-активные компоненты способна создавать, в присутствии пористого тела с развитой поверхностью, устойчивые коллоидные растворы (студнеобразные пленки), частично или полностью перекрывающие поры. Чтобы разрушить коллоидную структуру, необходим некоторый минимальный перепад давления g. Аналогичное явление при фильтрации воды в глинистых породах, где возникают глинистые коллоидные растворы. Экспериментально установлено, что порог фильтрации gменяется в широких пределах и тем выше, чем больше глинистого материала в пористой среде и чем выше остаточная водонасыщенность газо-водяной смеси.

Наиболее простой нелинейный закон фильтрации неньютоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом, имеет вид:

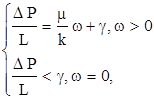
где: g - поровое значение градиента, ниже которого фильтрации нет.

Дата добавления: 2014-01-15