
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введення
|
|
|
|
План.
1)
Властивості векторного добутку:
1) 
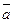 êê
êê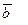
 ( умова колінеарності векторів );
( умова колінеарності векторів );
2) 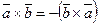 ;
;
3) 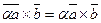 ;
;
4)  ;
;
Якщо вектори задано їхніми координатами  і
і 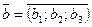 , то
, то 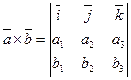
Геометричний зміст векторного добутку векторів: модуль векторного добутку дорівнює площині паралелограма, побудованого на сторонах як на векторах.
3.5 Мішаний добуток векторів.
Означення. Мішаним добутком векторів  упорядкованої трійки векторів
упорядкованої трійки векторів  ,
,  і
і  називається число, яке дорівнює векторному добутку
називається число, яке дорівнює векторному добутку 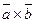 , помноженому скалярно на вектор
, помноженому скалярно на вектор  .
.

Якщо вектори 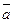 ,
,  ,
,  задано своїми координатами
задано своїми координатами  ,
, 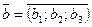 ,
, 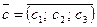 , то їх мішаний добуток визначають за формулою
, то їх мішаний добуток визначають за формулою

Властивості мішаного добутку:
1.  .
.
2.  .
.
Геометричний зміст мішаного добутку векторів: модуль мішаного добутку векторів 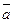 ,
,  і
і  дорівнює об’єму паралелепіпеда, побудованого на цих векторах
дорівнює об’єму паралелепіпеда, побудованого на цих векторах

а об’єм відповідної піраміди  .
.
3.6 Базис.
Означення. Лінійною комбінацією векторів 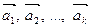 з дійсними коефіцієнтами
з дійсними коефіцієнтами  називається довільний вектор
називається довільний вектор 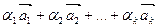 .
.
Якщо вектор поданий у вигляді лінійної комбінації деяких векторів, то кажуть, що він розкладений за цими векторами.
Означення. Вектори 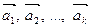 називаються лінійно залежними, якщо існують такі числа
називаються лінійно залежними, якщо існують такі числа  , що
, що  і
і  .
.
Якщо рівність  справджується лише при
справджується лише при  , то вектори
, то вектори 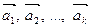 називаються лінійно незалежними.
називаються лінійно незалежними.
Два колінеарні вектори – лінійно залежні, а два не колінеарні вектори – лінійно незалежні.
Три компланарні вектори – лінійно залежні, а три не компланарні вектори – лінійно незалежні. Чотири вектори в тривимірному просторі завжди лінійно залежні.
Означення. Базисом  векторів на площині називається упорядкована пара лінійно незалежних (неколінеарних) векторів
векторів на площині називається упорядкована пара лінійно незалежних (неколінеарних) векторів 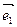 і
і  .
.
Всякий вектор  можна подати у вигляді суми
можна подати у вигляді суми 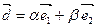 . Числа
. Числа 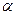 і
і  називають координатами вектора
називають координатами вектора  у базисі
у базисі  і пишуть
і пишуть 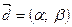 , сума
, сума 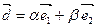 - розклад вектора за цим базисом.
- розклад вектора за цим базисом.
|
|
|
Означення. Базисом 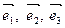 у просторі називається упорядкована трійка лінійно незалежних (некомпларних) векторів.
у просторі називається упорядкована трійка лінійно незалежних (некомпларних) векторів.
Всякий вектор  простору можна розкласти за базисом
простору можна розкласти за базисом 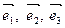 :
:  ,
, 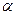 ,
, ,
, 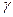 називають координатами вектора
називають координатами вектора  у цьому базисі пишуть
у цьому базисі пишуть  .
.
Необхідна і достатня умова компланарності або лінійної залежності векторів 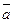 ,
,  і
і  виражається рівністю
виражається рівністю  .
.
Якщо 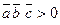 , то упорядкована трійка векторів
, то упорядкована трійка векторів 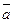 ,
,  і
і  права (мал.1), а якщо
права (мал.1), а якщо 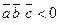 , то ліва (мал. 2).
, то ліва (мал. 2).
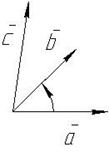
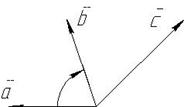
мал. 1. мал.2.
Приклад. Дано:  ,
,  ,
,  . Перевірити чи утворюють дані вектори базис. Якщо так, то знайти координати вектора
. Перевірити чи утворюють дані вектори базис. Якщо так, то знайти координати вектора 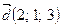 в цьому базисі.
в цьому базисі.
1) знайдемо мішаний добуток даних векторів:
 , значить дані вектори некомпланарні, тобто утворюють базис.
, значить дані вектори некомпланарні, тобто утворюють базис.
2) Виразимо вектор  через вектори
через вектори 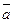 ,
,  ,
,  :
: 

Складаємо систему рівнянь 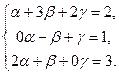 Þ
Þ  ;
; 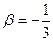 ;
; 
Отже 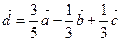 ,
, 
3.7 Ділення відрізка у даному відношенні.
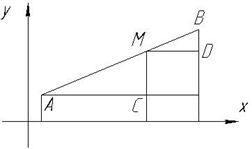 Задані точки
Задані точки  і
і  . Знайти координати точки
. Знайти координати точки  , що лежить на прямій АВ і ділить відрізок АВ у відношенні
, що лежить на прямій АВ і ділить відрізок АВ у відношенні 
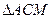 ~
~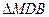 :
: 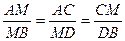 Þ
Þ 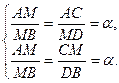 Þ
Þ 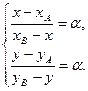
З першої рівності системи маємо:
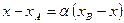
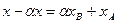


Аналогічно з другого рівняння системи знаходимо: 
Отже 
Якщо  , то
, то  ,
, 
Контрольні запитання.
1. Що називається вектором?
2. Які вектори називаються колінеарними?
3. Які дії виконуються над векторами в геометричній формі? Пояснити на прикладах.
4. Які дії виконуються над векторами в координатній формі? Пояснити на прикладах.
5. Що називається скалярним добутком векторів?
6. Сформулювати властивості скалярного добутку векторів.
7. Що називається векторним добутком векторів?
8. Сформулювати властивості векторного добутку векторів.
9. Що називається мішаним добутком векторів?
10. Що називається базисом?
11. Які вектори називаються компланарними?
12. Як обчислити координати точки, яка ділить даний відрізок у даному відношенні?
Лекція 4. Пряма на площині
|
|
|
1. Введення.
2. Пряма на площині. Відповідні рівняння (*).
3. Взаємне розміщення прямих на площині (*).
4. Нормальне рівняння прямої (*).
Поняття лінії є одним з найскладніших понять математики.
Рівнянням лінії в декартових координатах на площині називається рівняння виду 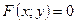 , яке задовольняють координати
, яке задовольняють координати 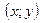 будь – якої точки цієї лінії і не задовольняють координати будь – якої точки, що не належить цій лінії.
будь – якої точки цієї лінії і не задовольняють координати будь – якої точки, що не належить цій лінії.
4.2 Загальне рівняння прямої
У прямокутній системі координат пряма лінія задається рівнянням першого степеня відносно х і у.
Ах + Ву + С = 0,
і навпаки, дане рівняння при довільних А, В, С (А і В одночасно не дорівнюють нулю) визначає деяку пряму в прямокутній системі координат Оху.
Вказане рівняння називається загальним рівнянням прямої лінії.
Дослідимо це рівняння.
Якщо А=0, 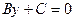
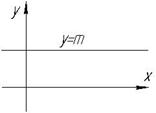

 - рівняння прямої, паралельної осі Ох.
- рівняння прямої, паралельної осі Ох.
 - рівняння осі абсцис (Ох)
- рівняння осі абсцис (Ох)
Якщо В=0, то 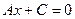 , то
, то
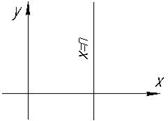
 - рівняння прямої, паралельної осі Оу
- рівняння прямої, паралельної осі Оу
Якщо: 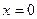 - рівняння осі ординат (Оу)
- рівняння осі ординат (Оу)
4.3 Рівняння прямої у відрізках на осях



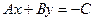
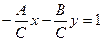





 Позначимо:
Позначимо:  , тоді
, тоді 
4.4 Рівняння прямої з кутовим коефіцієнтом


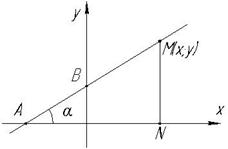
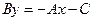
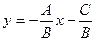
Позначимо 

ОВ=в – початкова координата,  - кутовий коефіцієнт прямої.
- кутовий коефіцієнт прямої.
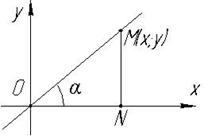 Якщо пряма проходить через початок координат, то
Якщо пряма проходить через початок координат, то 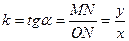
4.5 Рівняння прямої, що проходить через дві точки

Зафіксуємо на прямій дві точки  і
і  (координати відомі).
(координати відомі).
DАВС: 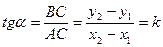
Отже 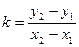 (1) - кутовий коефіцієнт прямої.
(1) - кутовий коефіцієнт прямої.
Зафіксуємо тепер точку  , а точка
, а точка 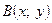 має поточні координати.
має поточні координати.
DАВС: 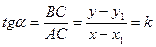
Отже 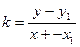 Þ
Þ  (2) - рівняння прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт.
(2) - рівняння прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт.
В рівняння (2) підставимо значення к з рівності (1)

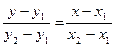 - рівняння прямої, що проходить через дві точки.
- рівняння прямої, що проходить через дві точки.
4.6 Взаємне розміщення прямих на площині.
Нехай прямі  і
і 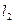 задані відповіднимирівняннями з кутовим коефіцієнтом:
задані відповіднимирівняннями з кутовим коефіцієнтом:
 ~
~ 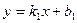

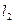 ~
~ 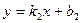
1) якщо  , то прямі перетинаються в одній точці;
, то прямі перетинаються в одній точці;
2) якщо  , то прямі мають однаковий кут нахилу до осі Ох, а значить паралельні.
, то прямі мають однаковий кут нахилу до осі Ох, а значить паралельні.
Доведення:  - кут між прямими
- кут між прямими  і
і 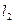 ,
,  ,
, 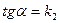 .
.

DАВС:  - зовнішній кут, тоді
- зовнішній кут, тоді 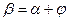 ,
, 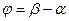

Отже  - тангенс кута між двома прямими.
- тангенс кута між двома прямими.
Якщо прямі  і
і 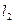 паралельні, то
паралельні, то  ,
,  Þ
Þ 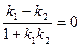 Þ
Þ  .
.
Якщо прямі  і
і 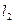 перпендикулярні, то
перпендикулярні, то  Þ
Þ  - не існує, тоді
- не існує, тоді 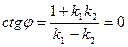 Þ
Þ 
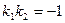

4.7 Нормальне рівняння прямої.
Нехай  - це пряма,
- це пряма,  - перпендикуляр(відстань), проведений від початку координат до прямої,
- перпендикуляр(відстань), проведений від початку координат до прямої, 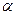 - кут нахилу цього перпендикуляра до осі Ох,
- кут нахилу цього перпендикуляра до осі Ох,  - довільна точка прямої.
- довільна точка прямої.
|
|
|
 Позначимо
Позначимо  ,
,  ,
,  ,
,  ,
,  .
.
З DАОМ: 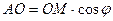
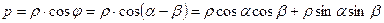
DВОМ: 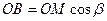
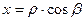
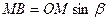
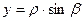
Тоді 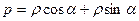
 - нормальне рівняння прямої.
- нормальне рівняння прямої.
(нормаль – перпендикуляр).
Знайдемо зв’язок між загальним рівнянням прямої та нормальним рівнянням прямої:

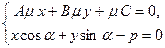 Þ
Þ 
Піднесемо до квадрату перші два рівняння і додамо почленно
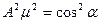
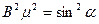
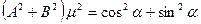

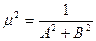
 - нормуючий множник
- нормуючий множник
Підставимо 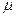 в рівність
в рівність 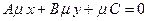 , отримаємо
, отримаємо 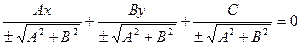 - нормальне рівняння прямої.
- нормальне рівняння прямої.
З рівності 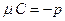 можна зробити слідуючи висновки:
можна зробити слідуючи висновки:
1) 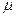 і
і  мають різні знаки (бо
мають різні знаки (бо 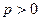 ,
,  - відстань);
- відстань);
2) в нормальному рівнянні прямої знак 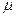 (знак перед квадратним коренем) беремо протилежний до С.
(знак перед квадратним коренем) беремо протилежний до С.
Щоб знайти відстань від точки 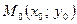 до прямої
до прямої  необхідно:
необхідно:
- записати нормальне рівняння прямої;
- в це рівняння підставити координати точки, відстань від якої ми знаходимо;
- взяти одержану відповідь по модулю.
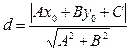
Контрольні запитання.
1. Виведіть відповідні рівняння прямої на площині.
2. Які умови паралельності і перпендикулярності прямих?
3. Виведіть нормальне рівняння прямої.
4. Як знайти відстань від даної точки до даної прямої?
Лекція 5. Площина і пряма у просторі.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 624; Нарушение авторских прав?; Мы поможем в написании вашей работы!