
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад. 26. Основні теореми диференціального числення (**)
|
|
|
|
План.
Вступ.
План.
25. Вступ.
26. Основні теореми диференціального числення (**).
27. Зростання та спадання функцій (**).
28. Екстремуми функцій (**).
29. Найбільше і найменше значення функції на відрізку (**).
30. Опуклість і вгнутість кривої. Точка перегину (**).
31. Алгоритм дослідження функції та побудови графіка (**).
Похідна функції має широке застосування при розв’язуванні різних задач математики, фізики, техніки та економіки. Так, наприклад, за допомогою похідної можна обчислити границю функції, знайти екстремум функції, інтервали монотонності, точки перегину функції та інше.
13.2 Основні теореми диференціального числення.
Теорема 1 (Теоерема Ферма). Якщо диференційовна на проміжку (а; b)
функція 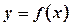 досягає найбільшого або найменшого значення у внутрішній точці
досягає найбільшого або найменшого значення у внутрішній точці 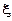 цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто:
цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто:

Доведення.
Припустимо, для визначеності, що набуває в точці
набуває в точці  найбільшого значення, тобто для всіх х з інтервалу (а; b) виконується умова:
найбільшого значення, тобто для всіх х з інтервалу (а; b) виконується умова:  .
.
За означенням похідної
 ,
,
причому ця границя не залежить від того, як наближається х до 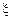 — справа чи зліва.
— справа чи зліва.
Розглянемо відношення 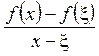 . Для всіх х, достатньо близьких до точки
. Для всіх х, достатньо близьких до точки 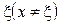 , маємо:
, маємо:

Перейдемо в останніх нерівностях до границі при  . Дістанемо:
. Дістанемо:
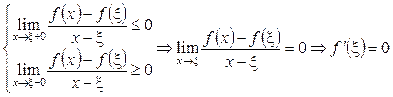 .
.
Аналогічно розглядається випадок, коли функція  набуває в точці
набуває в точці 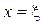 найменшого значення.
найменшого значення.
Геометричний зміст теореми Ферма:геометричний зміст похідної 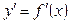 являє собою кутовий коефіцієнт дотичної до кривої
являє собою кутовий коефіцієнт дотичної до кривої  , звідси рівність нулю похідної
, звідси рівність нулю похідної  геометрично означає, що у відповідній точці цієї кривої дотична паралельна осі Ох.
геометрично означає, що у відповідній точці цієї кривої дотична паралельна осі Ох.
Теорема 2 (Теорема Ролля). Якщо функція f (х):
1) неперервна на відрізку [ a; b ];
|
|
|
2) диференційовна на інтервалі (а; b);
3) на кінцях сегмента набуває рівних між собою значень, тобто f (a) = f (b),
то на інтервалі (а; b) існує хоча б одна точка  , для якої
, для якої 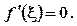

Геометричний зміст теореми Ролля: якщо крайні ординати неперервної кривої у = f (х), яка має в кожній точці дотичну, рівні, то на цій кривій знайдеться принаймні одна точка з абсцисою  , в якій дотична паралельна осі Ох.
, в якій дотична паралельна осі Ох.
Теорема 3 (Теорема Лагранжа). Якщо функція f (х):
1) неперервна на відрізку [ a; b ];
2) диференційовна на інтервалі (а; b),
то на інтервалі знайдеться хоча б одна точка  , така що:
, така що:

Геометричний зміст теореми Лагранжа: запишемо формулу у іншому вигляді:
 .
.

З малюнка бачимо, що величина  є тангенсом кута
є тангенсом кута  нахилу хорди, що проходить через точки А і В графіка функції
нахилу хорди, що проходить через точки А і В графіка функції
у = f (х) з абсцисами а і b.
Водночас,  — тангенс кута нахилу дотичної до кривої у точці С з абсцисою
— тангенс кута нахилу дотичної до кривої у точці С з абсцисою 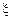 . Таким чином: якщо для всіх точок кривої у = f (х) існує дотична, то на цій кривій знайдеться точка з абсцисою
. Таким чином: якщо для всіх точок кривої у = f (х) існує дотична, то на цій кривій знайдеться точка з абсцисою 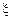 , в якій дотична паралельна хорді АВ, що сполучає точки А і В.
, в якій дотична паралельна хорді АВ, що сполучає точки А і В.
Теорема 3 (Теорема Коші). Якщо f (x) і 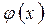 дві функції:
дві функції:
1) неперервні на відрізку [ a; b ];
2) диференційовні на інтервалі (а; b);
3)  для
для  ,
,
то на інтервалі (а; b) знайдеться хоча б одна точка 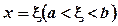 , така що
, така що
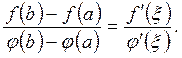
13.3. Зростання та спадання функцій.
Нагадаємо, що функція f (x) називається зростаючою на проміжку, якщо більшому значенню аргументу відповідає більше значення функції, тобто якщо  то
то 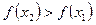 . Також функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції, тобто якщо
. Також функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції, тобто якщо 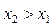 , то
, то 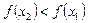 .
.
Теорема 1 (необхідна умова зростання (спадання) функції). Якщо диференційовна функція зростає (спадає) на деякому проміжку, то похідна цієї функції невід’ємна (недодатна) на цьому проміжку.
Теорема 2 (достатня умова зростання (спадання) функції). Якщо похідна диференційовної функції додатна (від’ємна) всередині деякого проміжку, то функція зростає (спадає) на цьому проміжку.
|
|
|
13.4. Екстремуми функцій.
Означення. При значенні х1 аргументу х функція f (х) має максимум f (х1), якщо в деякому околі точки х1 виконується нерівність 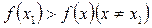 .
.
Аналогічно: при значенні х2 аргументу х функція f (х) має мінімум f (х2), якщо в деякому околі точки х2 виконується нерівність 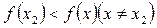 .
.

Максимум або мінімум функції називається екстремумом функції, а ті значення аргументу, при яких досягаються екстремуми функції, називаються точками екстремуму функції (відповідно точками максимуму або мінімуму функції). Екстремум функції, у загальному випадку, має локальний характер — це найбільше або найменше значення функції порівняно з ближніми її значеннями.
Теорема (необхідна умова екстремуму функції). У точці екстремуму диференційовної функції похідна її дорівнює нулю:
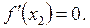
Геометрична умова означає, що в точці екстремуму диференційовної функції 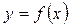 дотична до її графіка паралельна осі Ох:
дотична до її графіка паралельна осі Ох:
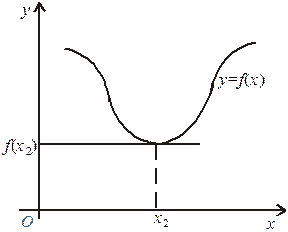
 Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не
Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не
існує.
Справді, якщо в точці х0 екстремуму функції 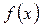 існує похідна
існує похідна 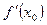 , то, згідно з даною теоремою, ця похідна дорівнює нулю. Те, що в точці екстремуму неперервної функції похідна може не існувати, показує приклад функції, графік якої має форму «ламаної».
, то, згідно з даною теоремою, ця похідна дорівнює нулю. Те, що в точці екстремуму неперервної функції похідна може не існувати, показує приклад функції, графік якої має форму «ламаної».
Ті значення аргументу х, які для заданої функції перетворюють на нуль її похідну  або для якої похідна
або для якої похідна  не існує (наприклад, перетворюється на нескінченність), називаються критичними значеннями аргументу (критичними точками).
не існує (наприклад, перетворюється на нескінченність), називаються критичними значеннями аргументу (критичними точками).
Із того, що  , не випливає, що функція
, не випливає, що функція  має екстремум при
має екстремум при 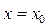 .
.
Наприклад, нехай 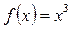 . Тоді
. Тоді  і
і  , однак значення
, однак значення  не є екстремумом даної функції.
не є екстремумом даної функції.
Отже, не для будь-якого критичного значення аргументу функції  має місце екстремум цієї функції. Через це поряд з необхідною умовою існують достатні умови існування екстремуму функції.
має місце екстремум цієї функції. Через це поряд з необхідною умовою існують достатні умови існування екстремуму функції.
Теорема 1 (достатня умова екстремуму функції). Нехай функція 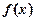 неперервна на деякому інтервалі, в якому міститься критична точка х0, і диференційовна в усіх точках цього інтервалу (крім, можливо, самої точки х0). Якщо при переході зліва направо через цю точку похідна:
неперервна на деякому інтервалі, в якому міститься критична точка х0, і диференційовна в усіх точках цього інтервалу (крім, можливо, самої точки х0). Якщо при переході зліва направо через цю точку похідна:
1) змінює знак з «+» на «–», то функція має у цій точці максимум;
|
|
|
2) змінює знак «–» на «+», то функція має у цій точці мінімум;
3) не змінює свого знака, то функція в точці х = х0 екстремуму не має.
Геометричну ілюстрацію теореми розглянемо на малюнку. Нехай у точці х = х1 маємо  і для всіх х, достатньо близьких до точки х1, виконуються нерівності
і для всіх х, достатньо близьких до точки х1, виконуються нерівності
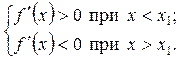
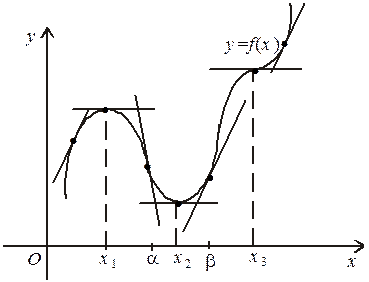
Тоді при 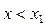 дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при
дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при  дотична утворює з віссю Ох тупий кут — функція спадає; при х = х1 функція переходить від зростання до спадання, тобто має максимум.
дотична утворює з віссю Ох тупий кут — функція спадає; при х = х1 функція переходить від зростання до спадання, тобто має максимум.
Якщо в точці х2 маємо  і для всіх значень х, достатньо близьких до точки х2, виконуються нерівності
і для всіх значень х, достатньо близьких до точки х2, виконуються нерівності
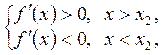
то при 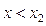 дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при
дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при  дотична до кривої утворює гострий кут — функція зростає. При х = х2 функція переходить від спадання до зростання, тобто має мінімум.
дотична до кривої утворює гострий кут — функція зростає. При х = х2 функція переходить від спадання до зростання, тобто має мінімум.
Якщо при х = х3 маємо 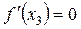 і для всіх значень х, достатньо близьких до х3, виконуються нерівності
і для всіх значень х, достатньо близьких до х3, виконуються нерівності 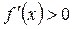 при
при 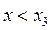 ;
;  при
при 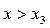 , то функція зростає як при
, то функція зростає як при 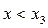 , так і при
, так і при  . Звідси при х = х3 функція не має екстремуму.
. Звідси при х = х3 функція не має екстремуму.
Зауваження. На основі даної теореми можна сформулювати таке правило для дослідження неперервної функції 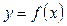 на максимум і мінімум.
на максимум і мінімум.
1. Знаходимо першу похідну функції.
2. Обчислюємо критичні значення аргументу х (критичні точки), для цього:
- прирівнюємо першу похідну до нуля і знаходимо дійсні корені здобутого рівняння 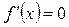 ;
;
- знаходимо значення х, для яких похідна 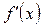 має розрив.
має розрив.
3. Досліджуємо знак похідної ліворуч і праворуч від кожної кри-
тичної точки
4. Обчислюємо значення функції  у кожній критичній точці.
у кожній критичній точці.
Теорема 2 (достатня умова екстремуму функції). Якщо для диференційовної функції 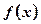 у деякій точці х0 її перша похідна
у деякій точці х0 її перша похідна 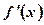 дорівнює нулю, а друга похідна
дорівнює нулю, а друга похідна 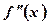 існує й відмінна від нуля, тобто
існує й відмінна від нуля, тобто  ,
, 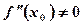 , то:
, то:
1) якщо друга похідна  , то в точці х0 функція
, то в точці х0 функція 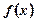 має мінімум;
має мінімум;
2) якщо  — максимум;
— максимум;
3) якщо 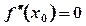 — питання залишається відкритим, і для його розв’язання треба застосувати перше правило.
— питання залишається відкритим, і для його розв’язання треба застосувати перше правило.
Зауваження. Для критичних точок, в яких похідна функції не
існує або дорівнює нескінченності, друге правило не застосовується.
|
|
|
Приклад. Дослідити на максимум і мінімум функцію  .
.
1. Знаходимо першу похідну 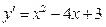 .
.
2. Знаходимо дійсні корені рівняння 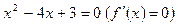 . Звідки
. Звідки 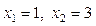 .
.
3. Досліджуємо критичні значення. Для цього область визначення функції 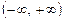 здобутими критичними точками розбиваємо на три інтервали
здобутими критичними точками розбиваємо на три інтервали 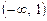 , (1, 3), (
, (1, 3), (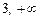 ). Виберемо в кожному інтервалі по одній точці і обчислимо значення похідної в цих точках:
). Виберемо в кожному інтервалі по одній точці і обчислимо значення похідної в цих точках:
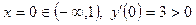 ;
;
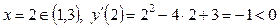 ;
;
 .
.
Знак похідної на кожному з трьох інтервалів збігається зі знаком похідної в обраній точці відповідного інтервалу.
| х | (– ¥, 1) | (1, 3) | (3, + ¥) | ||
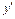
| + | – | + | ||
 у у
| 
| 
|
З таблиці видно: при переході (зліва направо) через значення
х = 1 похідна змінює знак з «+» на «–». Звідси, при х = 1 функція має максимум:
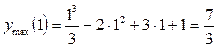 .
.
При переході через значення х = 3 похідна змінює знак з «–» на «+». Звідси, при х = 3 функція має мінімум:
 .
.
На інтервалі:  — функція зростає; (1, 3) — спадає; 3)
— функція зростає; (1, 3) — спадає; 3) 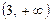 — зростає.
— зростає.
Другий спосіб. За допомогою другої похідної зробимо дослідження функції 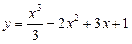 на екстремум.
на екстремум.
Перша похідна цієї функції  перетворюється в нуль у точках х = 1 і х = 3 (див. попередній приклад).
перетворюється в нуль у точках х = 1 і х = 3 (див. попередній приклад).
Друга похідна  :
:
а) при х = 1  , звідси в точці х = 1 функція має максимум
, звідси в точці х = 1 функція має максимум 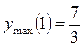 ;
;
б) при х = 3  , тобто в точці х = 3 функція має мінімум
, тобто в точці х = 3 функція має мінімум 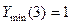 .
.
13.5. Найбільше і найменше значення функції на відрізку.
Якщо функція 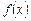 неперервна на проміжку [ a; b ], то вона набуває на цьому проміжку свого найбільшого й найменшого значення.
неперервна на проміжку [ a; b ], то вона набуває на цьому проміжку свого найбільшого й найменшого значення.
Найбільше значення функції на проміжку [ a; b ] називається абсолютним максимумом, а найменше — абсолютним мінімумом.
Припустимо, що на даному проміжку функція  має скінченне число критичних точок. Якщо найбільше значення досягається в середині проміжку [ a; b ], то очевидно, що це значення буде одним із максимумів функції (якщо існує кілька максимумів), точніше — найбільшим максимумом. Однак можливо, що найбільше значення досягатиметься на одному з кінців проміжку.
має скінченне число критичних точок. Якщо найбільше значення досягається в середині проміжку [ a; b ], то очевидно, що це значення буде одним із максимумів функції (якщо існує кілька максимумів), точніше — найбільшим максимумом. Однак можливо, що найбільше значення досягатиметься на одному з кінців проміжку.
Таким чином, функція на відрізку [ a, b ] досягає свого найбільшого значення на одному з кінців цього проміжку або в такій точці його, яка є точкою максимуму.
Аналогічне твердження можна сформулювати й про найменше значення функції: воно досягається на одному з кінців даного проміжку або в такій внутрішній точці, яка є точкою мінімуму.
Правило. Якщо треба знайти найбільше значення неперервної функції на проміжку [ a, b ], то необхідно:
1) знайти всі максимуми функції на проміжку;
2) визначити значення функції на кінцях проміжку, тобто обчислити f (a) і f (b);
3) з усіх отриманих значень функції вибрати найбільше: воно й буде найбільшим значенням функції на проміжку.
Аналогічно треба діяти і при визначенні найменшого значення функції на проміжку.
Приклад. Визначити на проміжку  найбільше й найменше значення функції
найбільше й найменше значення функції  .
.
1. Знаходимо максимуми й мінімуми функції на проміжку  :
:
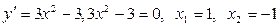 ;
;
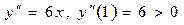 .
.
Таким чином, у точці х = 1 маємо мінімум:  .
.
Далі, 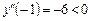 , тобто в точці х = = –1 маємо максимум:
, тобто в точці х = = –1 маємо максимум: 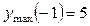 .
.
2. Визначаємо значення функції на кінцях проміжку:
 .
.
3. Таким чином, найбільше значення заданої функції на проміжку  є:
є:  , а найменше —
, а найменше —  .
.
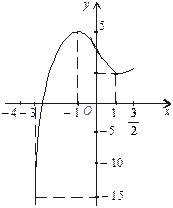
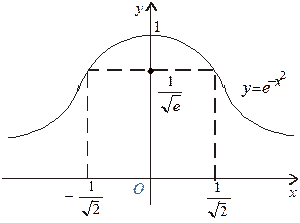
Графік функції зображено на малюнку:
13.6. Опуклість і вгнутість кривої. Точка перегину
Означення. Крива на проміжку називається опуклою (угнутою), якщо всі точки кривої лежать нижче (вище) будь-якої її дотичної на цьому проміжку.

З графіка функції 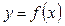 , який показано на малюнку бачимо: крива
, який показано на малюнку бачимо: крива 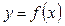 є опуклою на проміжку (а, с) і вгнутою на проміжку (с, b).
є опуклою на проміжку (а, с) і вгнутою на проміжку (с, b).
Означення. Точка, яка відокремлює опуклу частину кривої від вгнутої, називається точкою перегину.
На малюнку графіка функції, що наведено раніше, точка М — точка перегину.
Розглянемо дві теореми.
Теорема 1. 1) Якщо в усіх точках проміжку (с, b) для функції 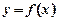 друга її похідна додатна
друга її похідна додатна 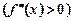 , то графік функції вгнутий.
, то графік функції вгнутий.
2) Якщо в усіх точках проміжку (а, с) друга похідна від’ємна  , то графік функції випуклий.
, то графік функції випуклий.
Теорема 2. Якщо для функції  друга похідна її
друга похідна її  у деякій точці х 0 перетворюється на нуль або не існує й при переході через цю точку змінює свій знак на обернений, то точка
у деякій точці х 0 перетворюється на нуль або не існує й при переході через цю точку змінює свій знак на обернений, то точка 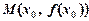 є точкою перегину графіка функції.
є точкою перегину графіка функції.
Зауваження. Якщо у точці х 0 друга похідна 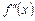 дорівнює нулю або не існує, але при переході через цю точку
дорівнює нулю або не існує, але при переході через цю точку 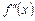 не змінює свого знака, то точка
не змінює свого знака, то точка  не є точкою перегину.
не є точкою перегину.
Приклад. Знайти інтервали опуклості та вгнутості графіка функції 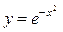 .
.
Маємо  .
.
Друга похідна  перетворюється в нуль, коли
перетворюється в нуль, коли
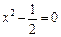 , звідки
, звідки  .
.
При переході через точки х 1 і х 2 друга похідна змінює знак.
Таким чином, точки  і
і 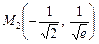 є точками перегину графіка функції.
є точками перегину графіка функції.
Результати дослідження заносимо в таблицю:
| х | 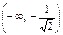
| 
| 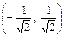
| 
| 
|

| + | – | + | ||
| у | È | Перегин | Ç | Перегин | È |
Із цієї таблиці бачимо, що графік функції на інтервалах  і
і  вгнутий, а на інтервалі
вгнутий, а на інтервалі  — опуклий.
— опуклий.
13.7 Алгоритм дослідження функції та побудови графіка.
При дослідженні функцій треба:
1. Знайти область визначення функції.
2. Встановити парність (непарність) і періодичність функції.
3. Знайти точки розриву функції та їх характер.
4. Визначити точки перетину графіка функції з осями координат.
5. Знайти точки екстремуму та обчислити значення функції у цих точках.
6. Визначити інтервали зростання й спадання функції.
7. Знайти точки перегину, інтервали випуклості й вгнутості.
8. Знайти асимптоти.
9. Знайти граничні значення функції, коли х прямує до граничних точок області визначення.
Графік функції будують за характерними точками й лініями, отриманими у результаті дослідження. Якщо їх недостатньо, знаходять допоміжні точки для деяких конкретних значень аргументу.
Приклад. Дослідити функцію  і побудувати її графік.
і побудувати її графік.
1. Знаходимо область визначення функції. Функція існує при всіх значеннях х за винятком значення х = 1. Звідси її область визначення: 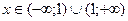 .
.
2. Точка х = 1 є точкою розриву функції. Дослідимо її характер:
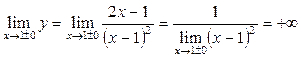 .
.
Як ліворуч, так і праворуч точки х = 1 маємо нескінченний розрив.
Точка х = 1 — точка розриву другого роду.
3. Вертикальні асимптоти. Пряма х = 1 є вертикальною асимптотою.
4. Знаходимо точки перетину графіка функції з осями координат:
- з віссю Ох: у = 0,  ;
;
- з віссю Оу: х = 0, 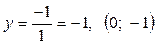 .
.
5. Знаходимо точки екстремуму та інтервали зростання і спадання функції, результати заносимо у таблицю:

 — критична точка.
— критична точка.
При  не існує, але у цій точці сама функція теж не існує.
не існує, але у цій точці сама функція теж не існує.
Дослідимо критичну точку х = 0 на екстремум:
при 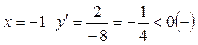 ;
;
при  .
.
| х | 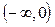
| (0, 1) | 
| ||
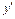
| – | + | Не існує | – | |
   у у
| y min (–1) | Не існує |
Проходячи через критичну точку зліва направо, похідна змінює знак з «–» на «+», через це в точці х = 0 функція має мінімум:
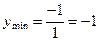 .
.
У точці х = 1 функція не визначена. При 
 , отже, функція на цьому інтервалі спадає.
, отже, функція на цьому інтервалі спадає.
6. Точки перегину та інтервали опуклості й вгнутості графіка функції знаходимо за допомогою другої похідної:

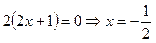 ; при х = 1
; при х = 1 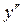 не існує, але в цій точці не існує і сама функція.
не існує, але в цій точці не існує і сама функція.
Дослідимо точку  :
:
при  ;
;
при 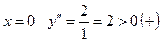 .
.
Друга похідна, проходячи через  , змінює знак, отже, точка перетину кривої з цією абсцисою є точкою перегину.
, змінює знак, отже, точка перетину кривої з цією абсцисою є точкою перегину.
Знайдемо її ординату:
 .
.
Таким чином, точка 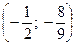 — точка перегину.
— точка перегину.
У точці х = 1 функція не визначена. При  , значить, графік функції вгнутий.
, значить, графік функції вгнутий.
Результати дослідження заносимо у таблицю:
| х | 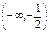
| 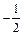
| 
| 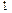
| 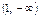
|
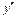
| + | + | Не існує | + | |
| у | Ç | Перегин (– 8/9) | È | Не існує | È |
7. Рівняння похилої асимптоти знаходимо у вигляді  :
:
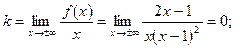

Таким чином, похилою асимптотою є у = 0 (вісь Ох).
На підставі результатів дослідження будуємо графік функції.

Контрольні запитання.
20. Сформулюйте теореми Ферма, Ролля і Лагранжа. Якій геометричний зміст вони мають?
21. Сформулюйте необхідну і достатню умову монотонності функції на інтервалі. Поясніть на прикладах.
22. Що називається екстремумом функції? Сформулюйте необхідну і достатню умову існування екстремума функції в певній точці.
23. Яка функція на проміжку називається опуклою та угнутою?
24. При виконанні яких вимог функція буде мати точку перегину на певному інтервалі?
Лекція 14. Невизначений інтеграл та його властивості.
32. Первісна та невизначений інтеграл (*).
33. Основні властивості невизначеного інтеграла (*).
34. Таблиця невизначених інтегралів (*).
35. Методи знаходження невизначених інтегралів (**).
14.1. Первісна та невизначений інтеграл
Означення. Функція F(x) називається первісною для функції f(x) на проміжку (а;b), якщо на цьому проміжку  або
або  .
.
Із означення виходить, що первісна F (x) — диференційовна, а значить неперервна функція на проміжку (а;b), і її вигляд суттєво залежить від проміжку, на якому вона розглядається.
Приклад. Первісні для функції 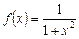 мають вигляд:
мають вигляд:
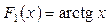 , бо
, бо 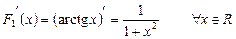 ;
;
 бо
бо  ;
;
 , бо
, бо  ,
,
причому F 1(x), F 2(x) — неперервні  , а F 3(x) у точці х = 0 має розрив.
, а F 3(x) у точці х = 0 має розрив.
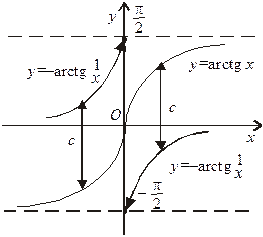
У цьому прикладі первісні F1 (x), F2(x), F3(x) знайдені методом добору із наступною перевіркою, з використанням таблиці похідних функцій.
Теорема. Якщо F (x) — первісна для функції f (x) на проміжку (а;b), то:
- F (x) + С — також первісна для f (x) на проміжку (а;b);
- будь-яка первісна Ф (х) для f (x) може бути подана у вигляді Ф (х) = F (x) + С на проміжку (а;b). (Тут С = const називається довільною сталою.)
Наслідок. Дві будь-які первісні для однієї й тієї самої функ-
ції на проміжку (а;b) відрізняються між собою на сталу величину.
Операція знаходження первісних для функції f (x) називається інтегруванням функції f (x). Задача інтегрування функції на проміжку полягає у тому, щоб знайти всі первісні функції на цьому проміжку, або довести, що функція не має первісних на цьому проміжку. Для розв’язування задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F (x), тоді (за теоремою про множину первісних) F (x) + С — загальний вигляд всієї множини первісних на цьому проміжку.
Означення. Функція F (x) + С, що являє собою загальний вигляд всієї множини первісних для функції f (x) на проміжку (а;b), називається невизначеним інтегралом від функції f (x) на проміжку (а;b) і позначається
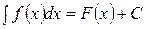 ,
, 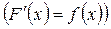 ,
,
де 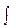 — знак невизначеного інтеграла;
— знак невизначеного інтеграла;
f (x) — підінтегральна функція;
f (x) dx — підінтегральний вираз;
dx — диференціал змінної інтегрування.
Геометричний зміст невизначеного інтеграла полягає в тому, що функція  є рівняння сім’ї кривих, які утворюються одна з одної паралельним перенесенням уздовж осі ординат.
є рівняння сім’ї кривих, які утворюються одна з одної паралельним перенесенням уздовж осі ординат.

Теорема ( теорема Коші ). Для існування невизначеного інтеграла для функції f (x) на певному проміжку достатньо, щоб f (x) була неперервною на цьому проміжку.
Зауваження. Виявляється, є такі невизначені інтеграли від елементарних функцій, які через елементарні функції не виражаються, наприклад:
 ,
, 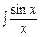 ,
,  ,
, 
існують у кожному із проміжків області визначення, але записати їх через основні елементарні функції не можна; в такому розумінні ці інтеграли називають «неінтегровними».
14.2 Основні властивості невизначеного інтеграла
1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції:
 ;
;
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:
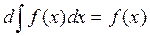 ;
;
3. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла, тобто:
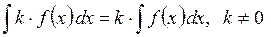
4. Невизначений інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують, тобто
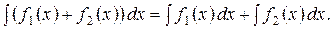
14.3 Таблиця основних інтегралів
1. 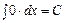 ; 2.
; 2.  ; 3.
; 3. 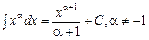 ;
;
4. 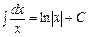 ; 5.
; 5.  ; 6.
; 6. 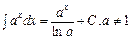 ;
;
7. 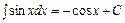 ; 8.
; 8. 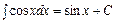 ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  ; 12.
; 12.  ;
;
13. 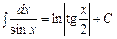 ; 14.
; 14. 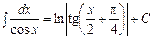 ;
;
15.  ;
;
16. 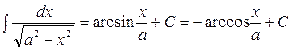 ;
;
17.  ;
;
18.  ;
;
19. 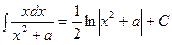 ;
;
20.  ;
;
21. 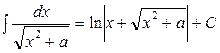 .
.
14.4 Методи знаходження невизначених інтегралів
14.4.1 Метод безпосереднього інтегрування
При безпосередньому інтегруванні використовується таблиця невизначених інтегралів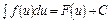 ,
,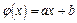 ,
, ..
..
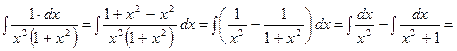

|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1363; Нарушение авторских прав?; Мы поможем в написании вашей работы!