
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дотична площина та нормаль
|
|
|
|
План.
План.
План.
46. Обчислення площ плоских фігур (**).
47. Обчислення об’ємів геометричних тіл. (**).
48. Довжина дуги кривої (**).
49. Площа поверхні тіла обертання (**).
18.1 Обчислення площ плоских фігур.
Якою б не була криволінійна фігура, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур.
І. Фігура обмежена лініями y=f(x), y = 0, x = a, x = b (мал. 1). Функція f(x) - неперервна та  Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така:
Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така:
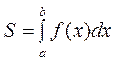 .
.
Якщо при виконанні всіх інших умов  (мал. 2), то
(мал. 2), то 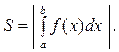

| 
| 
|
| Мал. 1 | Мал. 2 | Мал. 3 |
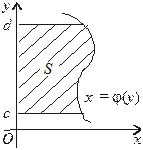
ІІ. Фігура обмежена лініями 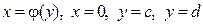 (мал. 3). Функція
(мал. 3). Функція  — неперервна та
— неперервна та  Площа S такої фігури буде:
Площа S такої фігури буде:

а якщо  (мал. 4), то:
(мал. 4), то:

ІІІ. Фігура обмежена лініями y=f(x), 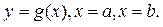 Функції f(x) та g(x) — неперервні та
Функції f(x) та g(x) — неперервні та 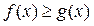 для
для  (мал. 5). Площа S такої фігури визначається як різниця площ фігур аА 2 В 1 b та аА 2 В 1 b:
(мал. 5). Площа S такої фігури визначається як різниця площ фігур аА 2 В 1 b та аА 2 В 1 b:


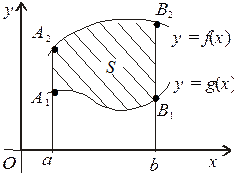
Мал. 4 Мал. 5
Приклад. Обчислити площу фігури, яка обмежена лініями 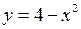 та
та 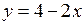 .
.
Побудуємо фігуру, як показано на малюнку. Для чого знайдемо точки перетину ліній. Для цього розв’яжемо систему:
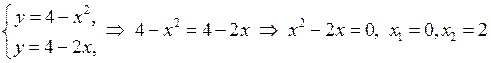 .
.
 Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких можна обчислити. Одержимо:
Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких можна обчислити. Одержимо:
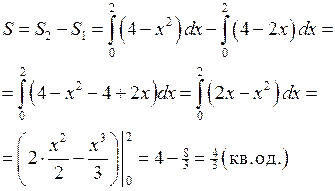
Якщо крива задана рівняннями в параметричній формі:




то площа криволінійної фігури обчислюється за
формулою
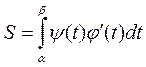
Дійсно, нехай рівняння визначають деяку у = f (x) на відрізку [ a; b ] і отже, площа криволінійної трапеції може бути обчислена за формулою
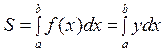
або
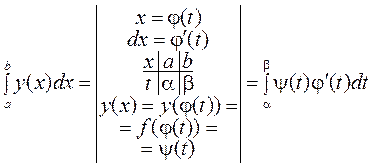 .
.
Приклад: Обчислити площу фігури, що обмежена віссю ОХ і однієї аркою циклоїди х = 5 (t – sint), y = 5 (1 – сost).
Проводимо обчислення за відповідною формулою:


Якщо фігура обмежена лінією у полярних координатах 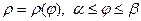 , де
, де  - неперервна і невід’ємна функція на
- неперервна і невід’ємна функція на 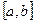 (
(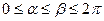 ). Тоді площу фігури можна обчислити за формулою:
). Тоді площу фігури можна обчислити за формулою:
|
|
|
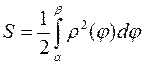


 18.2 Обчислення об’ємів геометричних тіл.
18.2 Обчислення об’ємів геометричних тіл.
Знайдемо об’єм тіла V утвореного обертанням навколо осі Ox фігури, обмеженої лініями 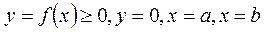 .
.

Встановлюємо, що площа поперечного перерізу S(x) в даному випадку є площа круга радіусом 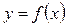 , тобто
, тобто  , а об’єм тіла обертання за формулою буде таким:
, а об’єм тіла обертання за формулою буде таким:
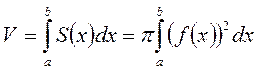
Аналогічно, об’єм тіла V утвореного обертанням навколо осі Оу фігури, обмеженої лініями x=0,  , y=c, y=d матиме вигляд:
, y=c, y=d матиме вигляд:
 .
.
|
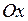 та
та 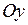 фігури, яка обмежена лініями
фігури, яка обмежена лініями  та
та 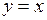 .
.
Обчислимо об’єми тіл, які утворюються при обертанні фігури навколо осей. Знайдемо точки перетину ліній:
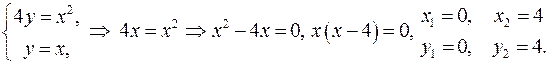
Одержали дві точки з координатами  та
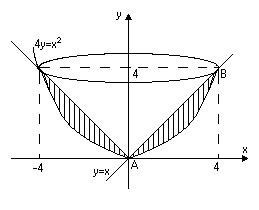
та 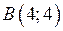 . Зобразимо ці тіла схематично як показано на малюнках:
. Зобразимо ці тіла схематично як показано на малюнках:

|
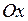 дорівнює різниці двох об’ємів тіл:
дорівнює різниці двох об’ємів тіл:

2) Аналогічно обчислюємо об’єм тіла обертання навколо осі 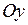 :
:

18.3 Довжина дуги кривої.
Нехай в прямокутних координатах на площині задана крива рівнянням у = f (x), де f (x) і f ¢(x) — неперервні на відрізку [ a; b ] функції.
Знайдемо довжину дуги АВ цієї кривої, що заключена між вертикальними прямими х = a i x = b.
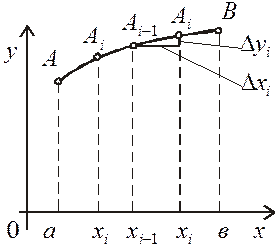
Введемо позначення D уі = f (xi) – f (xi– 1). Тоді:
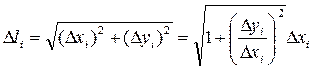 .
.
Далі за теоремою Лагранжа знаходимо:
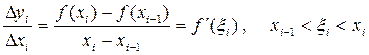
Отже,

Таким чином, довжина вписаної ламаної дорівнює:
 .
.
За умовою, f ¢(x) — неперервна, тому функція 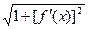 теж неперервна. Отже, існує границя написаної інтегральної суми, який дорівнює визначеному інтегралу:
теж неперервна. Отже, існує границя написаної інтегральної суми, який дорівнює визначеному інтегралу:
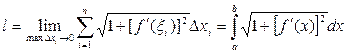
Якщо крива задана рівняннями в параметричній формі:
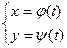 ,
,  ,
,  де j(t), y(t) — неперервні функції з неперервними похідними, причому j(t) ¹ 0, t Î [ a; b ]. В цьому випадку визначають деяку функцію у = f (t) — неперервну і мають неперервну похідну
де j(t), y(t) — неперервні функції з неперервними похідними, причому j(t) ¹ 0, t Î [ a; b ]. В цьому випадку визначають деяку функцію у = f (t) — неперервну і мають неперервну похідну
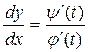 .
.
Нехай а = j(a), b = j(b). Тоді зробив в інтегралі підстановку х = j(t), dx = j¢(t)dx, отримаємо:
|
|
|
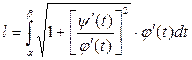
або

Приклад: Обчислити довжину дуги астроїди
х = 5cos3 t, y = 5sin3 t
Крива симетрична відносно обох координатних осей, тому обчислюємо спочатку довжину її четвертої частини, розташованої в першої чверті. Знаходимо
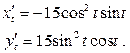
Параметр t буде змінюваться від 0 до  .
.
Отже:

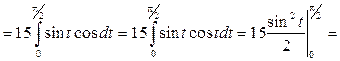
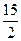 (од.)
(од.)

Зауваження. Якщо задана крива параметричними рівняннями у просторі:
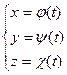 то довжина дуги обчислюється за формулою:
то довжина дуги обчислюється за формулою:
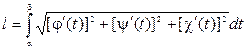
Якщо фігура обмежена лінією у полярних координатах 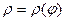 , де
, де 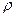 - полярний радіус,
- полярний радіус,  - полярний кут, то довжина дуги дорівнює:
- полярний кут, то довжина дуги дорівнює:

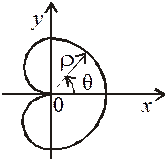
Приклад: Знайти довжину кардіоди 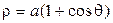 .
.
Змінюючи полярний кут q від 0 до p отримаємо половину шуканої довжини.
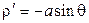 .
.

18.4 Площа поверхні тіла обертання.
 Нехай задана поверхня, утворена обертанням кривої у = f (х) навколо осі ОХ. Визначимо площу цієї поверхні на проміжку а £ x £ b.
Нехай задана поверхня, утворена обертанням кривої у = f (х) навколо осі ОХ. Визначимо площу цієї поверхні на проміжку а £ x £ b.
Проведемо хорди АМ 1, М 1 М 2, …, Мn -1 B довжини яких позначимо D l 1, l 2, …, D ln.
Кожна хорда довжини  при обертанні описує зрізаний конус, площа поверхні якого D Si дорівнює
при обертанні описує зрізаний конус, площа поверхні якого D Si дорівнює

Але 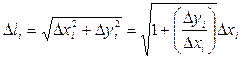 .
.
Застосовуючи теорему Лагранжа, отримаємо:

Отже,
 ,
,
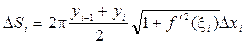
| Площа поверхні, що описана ламаною буде дорівнювати |

або

Тоді:

або

Приклад: Визначити площу поверхні параболоїда утвореного обертанням
навколо осі Ox дуги параболи у2 = 2рх, 0 £ х £ а.
Маємо:  .
.
Тоді:

Контрольні запитання.
39. Які стандартні випадки обчислення площ плоских фігур у декартових координатах можна навести?
40. Як обчислити площу плоскої фігури в полярних координатах та тоді, коли фігура обмежена лінією, що задана параметрично?
41. Запишіть формулу для обчислення об’єму тіла обертання. Поясніть її складові.
42. Запишить формули обчислення довжини дуги кривої для разних способів завдання лінії. Наведіть приклади.
43. Які знайти площу поверхні тіла обертання?
|
Лекція 19. Функція багатьох змінних.
50. Множина точок на площині та в n – вимірному просторі (*).
51. Означення функції багатьох змінних та способи її завдання (*).
52. Границя функції двох змінних (**).
53. Неперервність функції двох змінних (**).
19.1 Множина точок на площині та в n – вимірному просторі.
Упорядкованій парі чисел  на координатній площині відповідає одна точка
на координатній площині відповідає одна точка 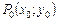 . Аналогічно, в n -вимірному просторі n упорядкованим дійсним числам відповідає одна точка
. Аналогічно, в n -вимірному просторі n упорядкованим дійсним числам відповідає одна точка  , де числа
, де числа 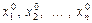 будуть координатами цієї точки.
будуть координатами цієї точки.
|
|
|
З метою скорочення запису далі розглядатимемо множини точок на площині, але подані далі означення можна вважати правильними і в разі n -вимірного простору.
Означення. Множина точок називається зв’язною, якщо будь-які її дві точки можна сполучити ламаною лінією так, щоб усі точки цієї лінії належали цій множині.
На малюнку а) буде зв’язна множина, а на малюнку б) — не зв’язна.

а) б)
Означення. Множина точок називається обмеженою, якщо всі її точки належать множині точок круга скінченного радіуса.
На малюнку а) маємо обмежену множину, а на малюнку б) — необмежену.
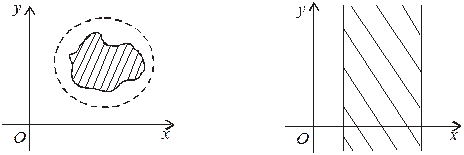
а) б)
Означення. Множина точок, координати яких задовольняють нерівність

називається d -околом точки  .
.
У випадку двовимірного простору записану нерівність можна подати у вигляді

|
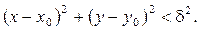
Вона визначає внутрішність круга з радіусом R=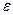 та з центром у точці P0(x0; y0).
та з центром у точці P0(x0; y0).
Якщо з d-околу точки P0, вилучимо саму точку P0, дістанемо виколотий d-окіл точки P0.
Означення. Точка називається внутрішньою для множини точок, якщо вона належить цій множині разом з деяким своїм d -околом, і зовнішньою, якщо існує її окіл з точок, жодна з яких не належить цій множині.
Означення. Зв’язна множина, яка складається тільки з внутрішніх точок, називається відкритою областю (або просто областю).
Область позначатимемо:
 .
.
(Читаємо: область D є множина точок площини з координатами (х; у), таких що 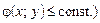
Означення. Точка називається межовою для області, якщо в будь-якому її d -околі існують точки, що не належать області і належать їй.
Означення. Множина межових точок називається межею області.
Означення. Область, об’єднана зі своєю межею, називається замкненою областю.
Означення. Множина називається опуклою, якщо будь-які точки множини можна зв’язати відрізком, який буде належати цій множині.
19.2 Означення функції багатьох змінних та способи її завдання.
Означення. Якщо кожній точці 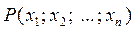 множини D
множини D
n -вимірного простору поставлено у відповідність за деяким
законом одне і тільки одне дійсне число 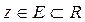 , то кажуть, що в області
, то кажуть, що в області 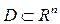 задано функцію n незалежних змінних
задано функцію n незалежних змінних  . При цьому D називають областю визначення функції, Е — областю значень функції.
. При цьому D називають областю визначення функції, Е — областю значень функції.
|
|
|
Згідно з означенням функцію 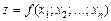 можна розглядати як функцію точки і записувати
можна розглядати як функцію точки і записувати 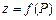 .
.
Зокрема, при n = 2 говорять, що задана функція двох змінних  , якщо кожній парі
, якщо кожній парі 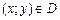 на площині поставлено у відповідність тільки одне число z.
на площині поставлено у відповідність тільки одне число z.
Способи завдання функції:
- аналітично – у вигляді формули – наприклад:  ;
;
- таблично – у вигляді таблиці – наприклад:
| у х | ||||
таблицею задана функція 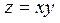 ;
;
- графічно – для графічного зображення функції двох змінних використовуємо систему координат Оxyz у тривимірному просторі.

Кожній парі чисел x та y відповідає точка P(x;y) площини Оxy. У точці  проводимо пряму, перпендикулярну до площини Оxy, та позначаємо на ній відповідне значення функції z; дістаємо в просторі точку Q з координатами
проводимо пряму, перпендикулярну до площини Оxy, та позначаємо на ній відповідне значення функції z; дістаємо в просторі точку Q з координатами  , яка позначається символом
, яка позначається символом  . Точки Q, які відповідають різним значенням незалежних змінних, утворюють певну поверхню у просторі. Така поверхня є графічним зображенням функції
. Точки Q, які відповідають різним значенням незалежних змінних, утворюють певну поверхню у просторі. Така поверхня є графічним зображенням функції 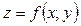 .
.
Зауваження. На практиці побудувати графік функції важко, адже йдеться про зображення на площині просторової фігури, а це не завжди вдається.
Приклад. Графічне зображення функції 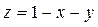 є площина, яка проходить через точки (0; 0; 1), (0; 1; 0), (1; 0; 0). Графічне зображення функції
є площина, яка проходить через точки (0; 0; 1), (0; 1; 0), (1; 0; 0). Графічне зображення функції  є півкуля.
є півкуля.

Існує й інший спосіб геометричного зображення функції двох змінних — зображення за допомогою ліній рівня.
Означення. Лінією рівня називається множина всіх точок площини, в яких функція 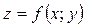 набуває однакових значень.
набуває однакових значень.
Рівняння ліній рівня записують у вигляді  . Накресливши кілька ліній рівня та зазначивши, яких значень набуває на них функція, дістанемо наближене уявлення про зміну функції. Елементарний приклад зображення функції за допомогою ліній рівня є зображення рельєфу місцевості на географічній карті. Висота місцевості над рівнем моря є функцією координат точки земної поверхні. За лініями рівня висоти, нанесеними на карту, легко уявити собі рельєф даної місцевості.
. Накресливши кілька ліній рівня та зазначивши, яких значень набуває на них функція, дістанемо наближене уявлення про зміну функції. Елементарний приклад зображення функції за допомогою ліній рівня є зображення рельєфу місцевості на географічній карті. Висота місцевості над рівнем моря є функцією координат точки земної поверхні. За лініями рівня висоти, нанесеними на карту, легко уявити собі рельєф даної місцевості.
19.3 Границя функції двох змінних.
Означення. Число B називається границею функції 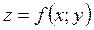 при
при  ,
,  , якщо для будь-якого
, якщо для будь-якого  існує число
існує число 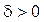 таке, що при виконанні нерівності
таке, що при виконанні нерівності 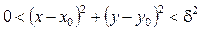 виконується нерівність
виконується нерівність 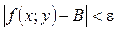 і позначається
і позначається  або
або 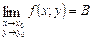 .
.
Зауваження. Для функції багатьох змінних справедливі
теореми про границю суми, добутку та частки, які анало-
гічні відповідним теоремам для функції однієї незалежної змінної.
Наведемо формулювання відповідних теорем.
Теорема 1. Якщо функція 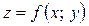 має границю при
має границю при  , то вона єдина.
, то вона єдина.
Теорема 2. Якщо функція  має границю при
має границю при 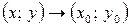 , то вона обмежена в деякому околі точки
, то вона обмежена в деякому околі точки  .
.
Теорема 3. Якщо:
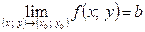
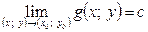
і в деякому околі точки 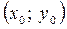 виконується нерівність
виконується нерівність  , то
, то  .
.
Теорема 4. Нехай 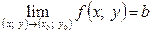 ,
,  .
.
Тоді:
1)  ;
;
2)  ;
;
3) 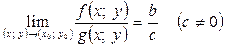 .
.
Зауваження. Між поняттями границі в точці для функції однієї змінної та функції багатьох змінних є багато спільного, але є й принципова відмінність, яка робить поняття границі функції кількох змінних суттєво більш обмеженим, ніж поняття границі функції однієї змінної.
Річ у тім, що коли  (
(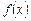 — функція однієї змінної), то це означає, що і лівостороння і правостороння границі дорівнюють b. Правильним є й обернене: з існування та збігу двох односторонніх границь випливає існування границі функції в точці.
— функція однієї змінної), то це означає, що і лівостороння і правостороння границі дорівнюють b. Правильним є й обернене: з існування та збігу двох односторонніх границь випливає існування границі функції в точці.
Для функції двох змінних  наближатися до точки
наближатися до точки 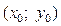 можна нескінченною множиною способів: і справа, і зліва, і зверху, і знизу, і під кутом 30° до осі Ох тощо.
можна нескінченною множиною способів: і справа, і зліва, і зверху, і знизу, і під кутом 30° до осі Ох тощо.
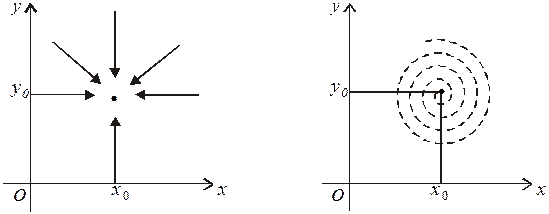
Більше того, до точки можна наближатися не тільки по прямій, а й по більш складних траєкторіях. Очевидно, що рівність  правильна тоді й тільки тоді, коли границя дорівнює b при наближенні до точки
правильна тоді й тільки тоді, коли границя дорівнює b при наближенні до точки  по будь-якій траєкторії. Це суттєво більш обмежене, ніж збіг двох односторонніх границь у випадку функції однієї змінної.
по будь-якій траєкторії. Це суттєво більш обмежене, ніж збіг двох односторонніх границь у випадку функції однієї змінної.
19.4 Неперервність функції двох змінних.
Означення. Функція 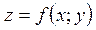 називається неперервною в точці
називається неперервною в точці 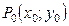 , якщо
, якщо 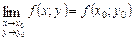 .
.
Означення. Функція 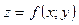 називається неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.
називається неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.
Таким чином, функція неперервна в точці 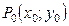 , якщо виконується водночас три умови:
, якщо виконується водночас три умови:
- функція визначена в цій точці та її певному околі;
- існує границя функції в цій точці 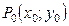 ;
;
- границя функції і відповідне значення функції в указаній точці рівні.
Означення. Нехай функція  визначена на мно-
визначена на мно-
жині Е, а змінні x і y, у свою чергу, залежать від змінних u
та v і  ,
,  , де обидві функції
, де обидві функції  та
та 
визначені на множині D. Якщо для будь-якого 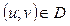 значення
значення  ,
,  такі, що
такі, що , то кажуть що на множині D визначена складна функція
, то кажуть що на множині D визначена складна функція  , де
, де  ,
, 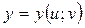 ; x, y — проміжні змінні, u, v — незалежні змінні.
; x, y — проміжні змінні, u, v — незалежні змінні.
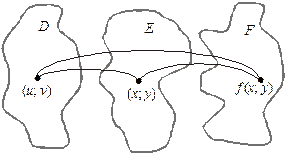
Теорема. Нехай на множині D визначено складну функцію  , де
, де 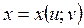 ,
, 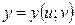 , і нехай функції
, і нехай функції  ,
, 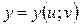 неперервні в точці
неперервні в точці  , а функція
, а функція 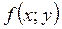 неперервна в точці
неперервна в точці  , де
, де  ,
, 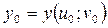 . Тоді складна функція
. Тоді складна функція  неперервна в точці
неперервна в точці  .
.
Властивості неперервної функції двох змінних:
- Якщо функція неперервна в точці, то вона обмежена деяким околом цієї точки.
- Якщо функції  та
та 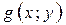 неперервні в точці
неперервні в точці 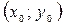 , то в цій точці будуть неперервними
, то в цій точці будуть неперервними  ,
,  ,
,  при
при 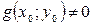 .
.
- Якщо функція  неперервна на замкненій обмеженій множині, то вона обмежена на цій множині.
неперервна на замкненій обмеженій множині, то вона обмежена на цій множині.
- Якщо функція  неперервна на замкненій обмеженій множині, то серед її значень на цій множині є як найменші, так і найбільші.
неперервна на замкненій обмеженій множині, то серед її значень на цій множині є як найменші, так і найбільші.
- Нехай функція 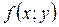 неперервна на зв’язній множині D і набуває у двох точках А і В цієї множини значень різних знаків. Тоді у множині D знайдеться така точка, що в ній функція перетворюється на нуль.
неперервна на зв’язній множині D і набуває у двох точках А і В цієї множини значень різних знаків. Тоді у множині D знайдеться така точка, що в ній функція перетворюється на нуль.
- Нехай функція 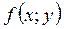 неперервна на зв’язаній множині D й у двох будь-яких точках А та В цієї множини набуває нерівних значень
неперервна на зв’язаній множині D й у двох будь-яких точках А та В цієї множини набуває нерівних значень 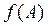 та
та 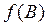 . Тоді на цій множині вона набуває будь-яких значень
. Тоді на цій множині вона набуває будь-яких значень 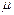 , яке лежить між
, яке лежить між 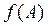 і
і 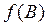 , тобто існує така точка
, тобто існує така точка  , що
, що 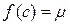 .
.
Контрольні запитання.
44. Дайте означення функції багатьох змінних. Якими способами її можна задати. Наведіть приклади.
45. Що називається границею функції двох змінних?
46. В якому випадку функція двох змінних буде неперервна?
|
Лекція 20. Диференційованість функції двох змінних.
54. Частинні та повний прирости функції двох змінних (*).
55. Диференційовність функції двох змінних (*).
56. Геометричний зміст частинних похідних (*).
57. Достатня умова диференційовності функції двох змінних у точці (*).
58. Диференціювання функцій (**).
59. Дотична площина та нормаль (**).
60. Частинні похідні і повні диференціали вищих порядків (**).
20.1 Частинні та повний прирости функції двох змінних.
Нехай функція 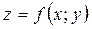 визначена в деякому околі точки
визначена в деякому околі точки  . Надамо незалежним змінним x та y приросту відповідно
. Надамо незалежним змінним x та y приросту відповідно 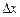 та
та  так, щоб точка
так, щоб точка  не виходила за межі вказаного околу. Тоді й точки
не виходила за межі вказаного околу. Тоді й точки 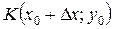 ,
,  також належатимуть розглядуваному околу.
також належатимуть розглядуваному околу.

Різницю  називають повним приростом функції
називають повним приростом функції 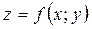 при переході від точки
при переході від точки 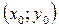 до точки
до точки  і позначають
і позначають  . Різницю
. Різницю  називають частинним приростом за х, а різницю
називають частинним приростом за х, а різницю  — частинним приростом за y функції
— частинним приростом за y функції 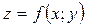 ; їх позначають відповідно
; їх позначають відповідно 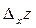 і
і 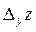 .
.
Таким чином,
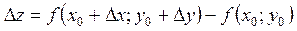 ,
,
 ,
, 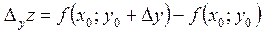
Аналогічно визначаються прирости функції більш ніж двох змінних.
20.2 Диференційовність функції двох змінних.
Означення. Функція  називається диференційовною у точці
називається диференційовною у точці 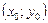 , якщо її повний приріст
, якщо її повний приріст  можна подати у вигляді:
можна подати у вигляді:
 ,
,
де А, В — числа, a, b — нескінченно малі при 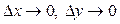 .
.
Головна лінійна частина приросту функції, тобто 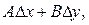 називається повним диференціалом функції (точніше першим диференціалом) двох змінних
називається повним диференціалом функції (точніше першим диференціалом) двох змінних 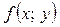 у точці
у точці  і позначається
і позначається 
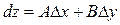 .
.
Теорема. Якщо функція 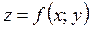 диференційовна в точці
диференційовна в точці  , тоді існують границі
, тоді існують границі 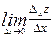 та
та 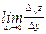 і вони дорівнюють відповідно А і В.
і вони дорівнюють відповідно А і В.
Означення. Нехай функція  визначена в точ-
визначена в точ-
ці  і в її деякому околі. Якщо існує границя
і в її деякому околі. Якщо існує границя  , то вона називається частинною похідною за х (за у) функції
, то вона називається частинною похідною за х (за у) функції 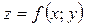 у точці
у точці  і позначається
і позначається  , або
, або  , або
, або 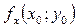 .
.
Таким чином,  ,
,  .
.
Із означення частинних похідних матимемо, що вони шукаються за тими правилами, що й похідні функції однієї змінної. Треба лише пам’ятати, що при знаходженні  змінна у вважається сталою, а при знаходженні
змінна у вважається сталою, а при знаходженні 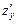 змінна х вважається сталою.
змінна х вважається сталою.
Тепер можна теорему можна сформулювати таким чином:
Теорема. (необхідна умова диференційовності функції  у точці). Якщо функція
у точці). Якщо функція  диференційовна в точці
диференційовна в точці 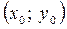 , то в цій точці існують частинні похідні
, то в цій точці існують частинні похідні 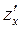 і
і 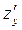 .
.
Диференціали незалежних змінних збігаються з їхніми приростами: 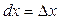 ,
,  . Тоді, як випливає із означення повного диференціала і розглянутої теореми повний диференціал функції
. Тоді, як випливає із означення повного диференціала і розглянутої теореми повний диференціал функції 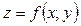 можна обчислити за формулою:
можна обчислити за формулою:
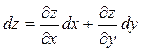
Аналогічно повний диференціал функції трьох аргументів  обчислюється за формулою:
обчислюється за формулою:
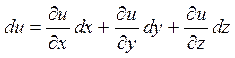
Приклад. Знайти  , якщо
, якщо 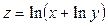 .
.
Тоді:
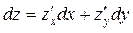 , де
, де 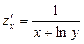 ;
; 
Отже,
 .
.
20.3 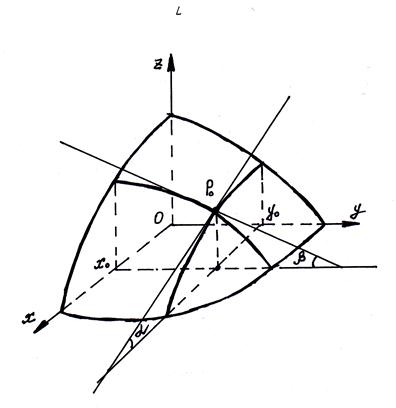 Геометричний зміст частинних похідних.
Геометричний зміст частинних похідних.
Якщо функцію  , що має частинні похідні в точці
, що має частинні похідні в точці  , розглядати за умови
, розглядати за умови  , то геометрично це означає, що поверхня
, то геометрично це означає, що поверхня 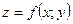 перетинається площиною
перетинається площиною  , паралельно координатній площині
, паралельно координатній площині  ; у перерізі дістаємо лінію. Тоді
; у перерізі дістаємо лінію. Тоді 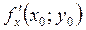 є кутовим коефіцієнтом дотичної до зазначеного перерізу в точці
є кутовим коефіцієнтом дотичної до зазначеного перерізу в точці  , тобто тангенсом кута нахилу цієї дотичної до додатного напряму осі Ох. Аналогічно,
, тобто тангенсом кута нахилу цієї дотичної до додатного напряму осі Ох. Аналогічно, 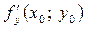 є кутовим коефіцієнтом дотичної, що проходить через точку
є кутовим коефіцієнтом дотичної, що проходить через точку  , до кривої, яка утворюється в результаті перетину поверхні
, до кривої, яка утворюється в результаті перетину поверхні  з площиною
з площиною 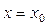 .
.
20.4 Достатня умова диференційовності функції двох змінних у точці.
Для функції однієї змінної твердження щодо її диференційовності та існування похідної є рівносильними. У випадку функції двох змінних ми маємо інше: існування частинних похідних — необхідна умова диференційовності функції в точці, але не є достатньою умовою диференційовності.
Теорема. Якщо функція  у деякому околі точки
у деякому околі точки  має неперервні частинні похідні, тоді вона диференційовна в точці
має неперервні частинні похідні, тоді вона диференційовна в точці 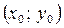 .
.
Можна навести твердження про зв’язок між поняттями неперервності і диференційовності функції двох змінних у точці, аналогічні до тих, що виконуються для функції однієї змінної.
Теорема. Якщо функція 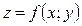 диференційовна в точці
диференційовна в точці  , то вона неперервна в цій точці.
, то вона неперервна в цій точці.
Обернене твердження неправильне.
20.5 Диференціювання функцій.
20.5.1 Похідна неявної функції.
Якщо існує неперервна функція однієї змінної  , така що відповідні пари
, така що відповідні пари  задовольняють умову
задовольняють умову  , тоді ця умова називається неявною формою функції
, тоді ця умова називається неявною формою функції 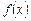 , а сама функція
, а сама функція 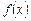 називається неявною функцією, яка задовольняє умову
називається неявною функцією, яка задовольняє умову 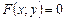 .
.
Припустимо, що неперервна функція  задана в неявній формі
задана в неявній формі 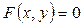 і що
і що  . Похідну
. Похідну 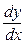 обчислюємо за формулою:
обчислюємо за формулою:
 ,
, 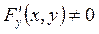
Приклад. Знайти похідну від неявної функції  –
– в точці
в точці 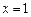 ,
,  .
.
Маємо  ,
,  , звідки
, звідки
 .
.
Для  ,
,  маємо
маємо  .
.
Аналогічно частинні похідні функції двох незалежних змінних  , яку задано за допомогою рівняння
, яку задано за допомогою рівняння 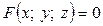 , де
, де  — диференційовна функція змінних x, y, z, можуть бути обчислені за формулами:
— диференційовна функція змінних x, y, z, можуть бути обчислені за формулами:
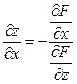 ,
, 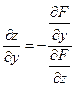 , за умови, що
, за умови, що  .
.
Приклад. Знайти 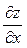 ,
,  , якщо
, якщо  .
.
У даному разі  . Знайдемо
. Знайдемо  ,
,  ,
,  .
.
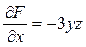 ,
,  ,
, 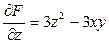 .
.
Тоді:
 ,
,  .
.
20.5.1 Похідна складної функції.
Теорема. Нехай на множині D визначена складна функція  , де
, де  ,
,  і нехай функції
і нехай функції  ,
,  мають у деякому околі точки
мають у деякому околі точки  неперервні частинні похідні, а функція
неперервні частинні похідні, а функція 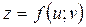 — неперервні частинні похідні в деякому околі точки
— неперервні частинні похідні в деякому околі точки  , де
, де 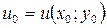 ,
,  . Тоді складна функція
. Тоді складна функція  диференційовна в точці
диференційовна в точці  , причому
, причому
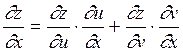

Приклад. Знайти 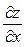 і
і  для функції
для функції  .
.
Маємо 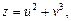 де
де 
 .
.
Тоді 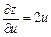 ,
,  ,
,  ,
,  ,
, 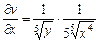 ,
,  .
.
Таким чином, 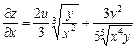 ,
,  , або після підставляння виразів u і v дістанемо
, або після підставляння виразів u і v дістанемо  ,
,  .
.
Якщо функція 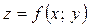 диференційовна в точці
диференційовна в точці  , то виконується рівність
, то виконується рівність
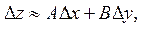
або
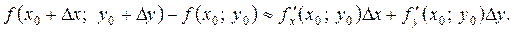
Узявши в цій наближеній рівності  ,
, 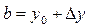 , дістанемо:
, дістанемо:
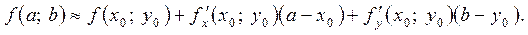
На отриманій формулі ґрунтується алгоритм використання диференціала для наближених обчислень.
Крім того, якщо взяти 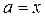 ,
,  , дістанемо:
, дістанемо:
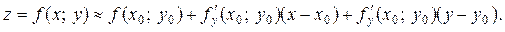
Це рівняння дотичної площини, що проходить через точку 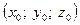 .
.
Якщо поверхню задано у просторі рівнянням 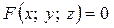 , то рівняння дотичної площини до поверхні
, то рівняння дотичної площини до поверхні  в точці
в точці  має вигляд:
має вигляд:
 ,
,
де 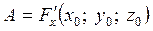 ,
, 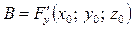 ,
,  .
.
Нормаль до поверхні в точці  — це пряма, що проходить через точку
— це пряма, що проходить через точку 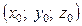 і перпендикулярна до дотичної площини.
і перпендикулярна до дотичної площини.
Отже, її рівняння
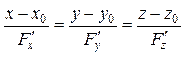 .
.
20.7. Частинні похідні і повні диференціали вищих порядків.
Нехай функція 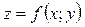 має частинні похідні в усіх точках множини
має частинні похідні в усіх точках множини 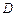 . Візьмемо будь-яку точку
. Візьмемо будь-яку точку 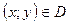 ; у цій точці існують частинні похідні
; у цій точці існують частинні похідні  і
і  , які залежать від x і y, тобто вони є функції двох змінних. Отже, можна ставити питання про знаходження їхніх частинних похідних. Якщо вони існують, то називаються похідними другого порядку і позначаються так:
, які залежать від x і y, тобто вони є функції двох змінних. Отже, можна ставити питання про знаходження їхніх частинних похідних. Якщо вони існують, то називаються похідними другого порядку і позначаються так:
 або
або  ,
,
 або
або  ,
,
 або
або  ,
,
 або
або  .
.
Аналогічно визначаються і позначаються частинні похідні третього і вищих порядків, наприклад:
 ,
, 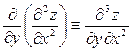 .
.
Означення. Диференціалом другого порядку від функції 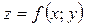 називається диференціал від її повного диференціала першого порядку, тобто
називається диференціал від її повного диференціала першого порядку, тобто  .
.
Аналогічно визначаються диференціали третього і вищих порядків

..........

Приклад. Знайти 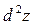 , якщо
, якщо  .
.





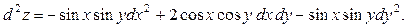
Приклад. Знайти  і
і  для функції
для функції  .
.
 ,
, 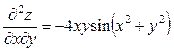 ,
,
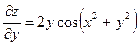 ,
, 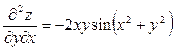 .
.
У попередньому прикладі ми дістали, що 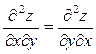 . Виявляється, що ця рівність виконується в багатьох випадках, що випливає з такої теореми.
. Виявляється, що ця рівність виконується в багатьох випадках, що випливає з такої теореми.
Теорема. Якщо функція  визначена в області D і в цій області існують перші похідні
визначена в області D і в цій області існують перші похідні  та
та  , а також другі мішані похідні
, а також другі мішані похідні  ,
, 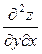 , які до того ж як функції від х і у неперервні в точці
, які до того ж як функції від х і у неперервні в точці 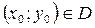 , то в цій точці:
, то в цій точці:
 .
.
Контрольні запитання.
1. Що називається частинними похідними та повним приростом функції двох змінних?
2. Сформулювати необхідну і достатню умови диференційованності функції двох змінних.
3. Поясніть геометричний зміст частинних похідних.
4. Записати рівняння дотичної площини та нормалі до певної поверхні в певній точці.
Лекція 21. Екстремум функції двох змінних. Найменьше і найбільше значення функції двох змінних.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1806; Нарушение авторских прав?; Мы поможем в написании вашей работы!
