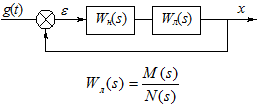Определение автоколебаний, анализ устойчивости

(нечётные нелинейности)

Периодическое колебательное решение в предположении g (t) = 0 (авто-колебание), ищем в виде

.

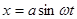Характеристическое уравнение гармонически линеаризованной системы имеет вид

1 + W_н W_л =0.

Алгебраический способ определения автоколебаний

Перепишем характеристическое уравнение в виде

.

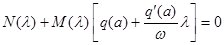Периодическое решение соответствует паре частот мнимых корней 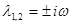этого характеристического уравнения.

Полагая 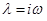, получим

.

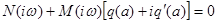Выделяя действительную и мнимую части уравнения, получим

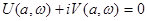(1)

откуда

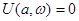и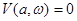

Имеем два уравнения с двумя неизвестными a и 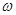, определяющими соответственно амплитуду и частоту собственного гармонического колебания нелинейной системы (т.е. a и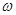автоколебания).

Обозначая

,

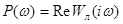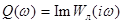
из условия

,

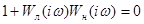получаем ещё одну форму записи уравнений для a и: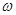

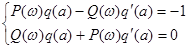. (2)

Для однозначных нелинейностей ()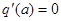

.

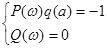т.е. частота автоколебаний определяется линейной частью системы.

Определив таким образом периодическое решение, надо исследовать его устойчивость. Если оно устойчиво, то это означает автоколебательный процесс.

Введём малые начальные отклонения 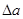амплитуды и 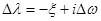собственных значений от их величин a и ω в гармоническом решении

. (3)

Этим выражением описывается колебательный переходный процесс вблизи чисто гармонического

.

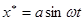Для устойчивости рассматриваемого гармонического процесса необходимо, чтобы

.

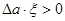Переходя от (3) к

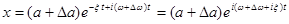
и используя (1), получаем

.

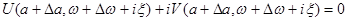Разлагая данное выражение в ряд Тейлора и учитывая, что

,

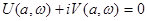имеем

.

Выделяя действительную и мнимую части получаем систему двух уравнений, а исключая 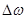и разрешая полученную систему относительно 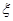,получим

.

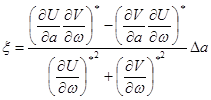Следовательно, для устойчивости требуется выполнение неравенства

(4)

В дополнение к этому нужно потребовать, чтобы в характеристическом уравнении гармонически линеаризованной системы

,

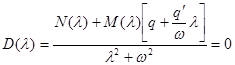все корни (кроме использованной нами пары чисто мнимых корней) имели отрицательные вещественные части, т.е. чтобы многочлен удовлетворяет критерию Раусса-Гурвица (или Михайлова).

Итак, критерием устойчивости периодического решения является неравенство (4) с добавлением вышеуказанного условия.

Частотно-графический способ определения автоколебаний

Амплитудно-фазовая характеристика разомкнутой системы имеет вид:

.

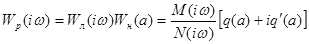Периодическому решению (колебательным корням) соответствует

.

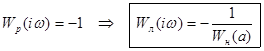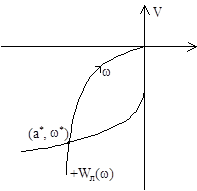Это уравнение определяет a и.

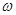Решается оно графически нанесением на плоскость { U,V } амплитудно-фазовой характеристики (АФХ) линейной части 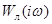, а также обратной АФХ нелинейности с противоположным знаком. Точка их пересечения и определяет величины a и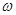, причём значение а отсчитывается по кривой 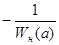, а значение 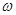– по кривой .

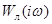Условия устойчивости определяются следующим образом. Придадим амплитуде отклонение 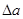. Система будет возвращаться к периодическому решению, если при 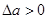колебания затухают, а при 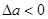- расходятся. Следовательно, при 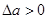характеристика 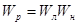должна деформироваться так, чтобы критерий Найквиста соблюдался, а при 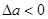- нарушался.

Определение вынужденных колебаний

Поскольку для нелинейных систем неприменим принцип суперпозиции, то, вообще говоря, в рассматриваемом случае нельзя складывать частные решения при различных внешних воздействиях, найденных по отдельности, а также складывать свободные и вынужденные колебания. Особое нелинейное сложение решений возможно, если решения отличаются по степени медленности протекания их по времени.

Ограничимся рассмотрением одночастотных вынужденных колебаний, когда эти колебания происходят с частотой внешнего периодического воздействия. Форма колебаний, как и прежде, на основании гипотезы фильтра, будет считаться близкой к синусоидальной для переменной x, от которой зависит нелинейная функция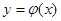. Существование одночастотных вынужденных колебаний во многих случаях обуславливаются некоторыми ограничениями на частоту и амплитуду внешнего воздействия, т.е. некоторыми условиями захвата (см. ниже). Будем предполагать выполнение этих условий.

Итак, рассмотрим следующую структурную схему:

, .

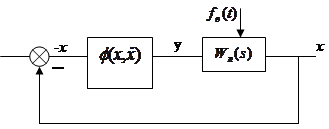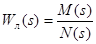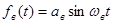Дифференциальное уравнение движения имеет вид (g(t)=0)

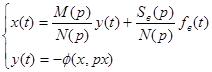
или

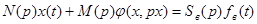
В предположении гипотезы фильтра, имеем

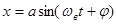. (5)

то есть, предполагаем, что вынужденное колебание отличается от внешнего воздействия фазой и амплитудой.

Далее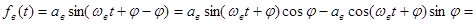

.

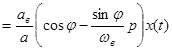Тогда

,

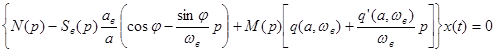где

.

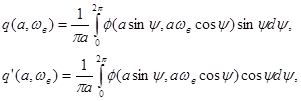
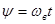Условное характеристическое уравнение имеет вид

.

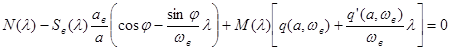Предполагаемое искомое решение (5)является гармоническим колебанием с амплитудой 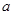и фазой j. Поэтому при подстановке величин 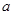и j в коэффициенты характеристического уравнения оно должно превратится в однородное уравнение с постоянными коэффициентами, имеющее пары корней .

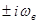Поэтому, заменяя l на 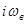, получим

.

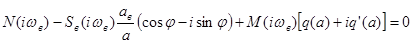Учитывая, что 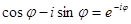, получаем искомое уравнение

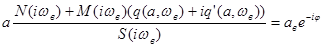(6)

Решая это уравнение, определяем 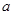и j. Если решение существует, то существует и искомое одночастотное колебание.

Это уравнение можно решать, например, графически.

Для каждого значения частоты 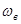входящего воздействия при заданных параметрах системы на комплексной плоскости строится кривая

.

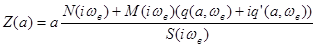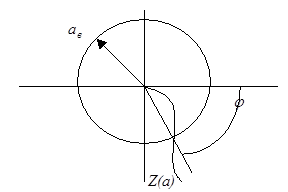Эта кривая соответствует левой части равенства (6). Правая часть изобразится в виде окружности радиуса .

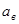Точка пересечения кривых даёт решение задачи, причём в точке пересечения по дуге окружности определяется фазовый сдвиг j, а по кривой Z (a) – величина амплитуды вынужденных колебаний.

Возможны случаи, когда окружности 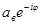пересекают кривую Z(a) только при радиусе 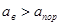. В этом случае одночастотные вынужденные колебания возможны только при достаточно большой амплитуде a_в. Это свойство называется условием захвата.

Дата добавления: 2014-01-15