Лекция семнадцатая

Расчёт статически неопределимых систем методом сил на температурное и кинематическое воздействие

17.1. Расчёт стержневых статически неопределимых систем на температурное воздействие

17.2. Пример расчёта статически неопределимой рамы на температурное воздействие в обычной форме

17.3. Пример расчёта статически неопределимой рамы на температурное воздействие в матричной форме

17.4. Расчёт стержневых статически неопределимых систем на кинематическое воздействие

17.5. Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

17.6. Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

17.7. Вопросы для самопроверки

17.8. Рекомендуемая литература

17.1. Расчёт стержневых статически неопределимых систем на температурное воздействие

На плоскую стержневую систему, степень статической неопределимости которой равна n (рис. 17.1,а) независимо друг от друга действует f вариантов температурных полей. Каждое температурное поле характеризуется изменением температуры на различных поверхностях элементов стержневой системы. На k-ом участке любого элемента сооружения величины приращений температуры 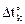, коэффициента линейного температурного расширения материала a_k, высоты поперечного сечения h_k, а также его жесткостных характеристик на изгиб EJ_k, сдвиг GA_k и растяжение–сжатие ЕА_k будем считать постоянными. Закон изменения приращений температуры по высоте поперечного сечения примем линейным (см. п. 12.2 второй части настоящего курса лекций).

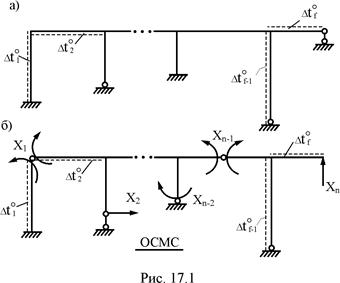
Образуем статически определимую основную систему метода сил (ОСМС), удалив из заданного сооружения n лишних связей (рис. 17.1,б). Неизвестные метода сил X₁, X₂, …, X_j, …, X_n определим из условия эквивалентности напряжённо-деформи­руе­мых состояний заданного сооружения (рис. 17.1,а) и его основной системы (рис. 17.1,б), т.е. из условий равенства нулю перемещений по направлению X_i (i = 1, 2, …, n) в основной системе метода сил от неизвестных этого метода и заданного изменения температуры.

Используя принцип независимости действия сил и повторяя выкладки, приведенные в п. 16.2 шестнадцатой лекции, получим систему канонических уравнений для определения неизвестных X₁, X₂, …, X_j, …, X_n в случае температурного воздействия на сооружение.

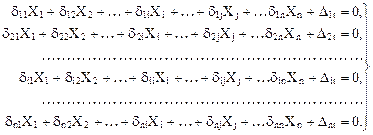(17.1)

Величина главных d_ii и побочных d_ij коэффициентов системы канонических уравнений (17.1) не зависят от вида воздействия на сооружения и определяются по ранее полученным в п. 16.2 формулам (16.5)–16.6) в общем случае плоских стержневых систем и по формулам (16.8)–(16.9) для рам и балок.

Свободные члены системы канонических уравнений (17.1) D_it представляют собой перемещения по направлению неизвестных метода сил X_i (i = 1, 2, …, n) в основной системе от заданного температурного воздействия. Так как для расчёта принята статически определимая основная система, указанные перемещения в ней определяются по формуле (12.4), полученной в п. 12.2 второй части настоящего курса лекций:

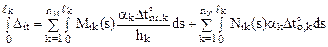. (17.2)

В соотношении (17.2) M_ik(s), N_ik(s) – соответственно, изгибающие моменты и продольные силы на участке, где происходит изменение температуры на величину 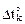, от X_i = 1 в основной системе метода сил. Напоминаем читателям, что параметрами, характеризующими температурное воздействие на k-ом участке, являются: 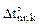– перепад приращений температуры по высоте поперечного сечения; 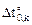– приращение температуры на уровне центра тяжести поперечного сечения.

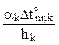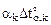При наличии эпюр внутренних усилий M_ik(s) и N_ik(s), а также условных эпюр и , построенных вдоль продольных осей элементов сооружения, интегралы, входящие в формулу (17.2), можно вычислить, используя правило Верещагина (см. п. 11.4 второй части настоящего курса лекций).

Жёсткости поперечных сечений элементов сооружения EJ_k, GA_k, EA_k учитываются при вычислении коэффициентов d_ii и d_ij системы канонических уравнений (17.1) и их значения не входят в соотношение (17.2), с помощью которого вычисляются свободные члены указанной системы уравнений. Отсюда следует, что величины усилий в лишних связях X_i и, следовательно, внутренних усилий в заданном сооружении являются функциями абсолютных значений жесткостных характеристик поперечных сечений стержней.

Получив значения усилий в лишних связях из системы уравнений (17.1), мы свели расчёт статически неопределимого сооружения (рис. 17.1,а) на температурное воздействие к расчёту статически определимой основной системы метода сил (рис. 17.1,б), на которую действуют указанные усилия X₁, X₂, …, X_i, …, X_j, …, X_n и заданное изменение температуры. Так как изменение температуры в статически определимых сооружениях внутренних усилий не вызывает (см. п. 12.1 второй части настоящего курса лекций), то значения изгибающих моментов M_t, поперечных и продольных сил Q_t и N_t в сечениях заданного сооружения в этой ситуации определяются только усилия X₁, X₂, …, X_i, …, X_j, …, X_n. Имея эпюры внутренних усилий M_j, Q_j, N_j от X_j = 1 в основной системе и используя принцип независимости действия сил, получим:

M_t = M₁X₁ + M₂X₂ + … + M_jX_j + … + M_nX_n,

Q_t = Q₁X₁ + Q₂X₂ + … + Q_jX_j + … + Q_nX_n, (17.3)

N_t = N₁X₁ + N₂X₂ + … + N_jX_j + … + N_nX_n.

Окончательные эпюры внутренних усилий M_t, Q_t, N_t построены правильно, если, выполнены кинематические условия: перемещение по направлению любого усилия X_i (i = 1, 2, …, n) в отброшенных связях в основной системе от действия всех неизвестных метода сил X₁, X₂, …, X_j, …, X_n и заданного температурного воздействия должны быть равны нулю, так как в заданном сооружении имеются связи, препятствующие перемещениям по направлению X_i.

Сопрягая проверяемые эпюры внутренних усилий M_t, Q_t, N_t с эпюрами внутренних усилий M_i, Q_i, N_i, построенными в основной системе от X_i = 1, в соответствии с соотношениями (17.3) вычислим перемещение по направлению X_i в статически определимой основной системе только от неизвестных метода сил X₁, X₂, …, X_j, …, X_n. Добавляя к этому перемещению ещё и перемещение от заданного изменения температуры D_it, получим полное перемещение по направлению X_i в основной системе, которое, если выполняется кинематическая проверка, т.е. если поставленная задача решена правильно, должно быть равно нулю. Это возможно, если перемещение по направлению X_i в основной системе, вызванное неизвестными методами сил, будет компенсировано перемещением в том же направлении от заданного температурного воздействия, т.е. будет равно (–D_it). Таким образом,

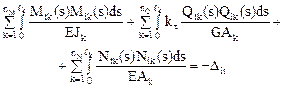. (17.4)

В матричной форме система канонических уравнений (17.1) запишется:

dХ + D_t = 0. (17.5)

d – матрица внешней податливости основной системы метода сил по направлению усилий в отброшенных связях X_i, или матрица коэффициентов при неизвестных метода сил системы канонических уравнений. Структура этой матрицы не зависит от типа воздействия на заданное сооружение. Её элементы вычисляются по формуле (16.21), полученной в п. 16.7 шестнадцатой лекции.

Х – матрица неизвестных метода сил.

.

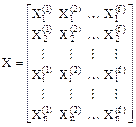D_t – матрица перемещений по направлению неизвестных метода сил в основной системе от заданного температурного воздействия, или матрица свободных членов системы канонических уравнений (17.1).

.

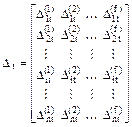Число строк в матрицах X и D_t равно степени статической неопределимости сооружения n, а число столбцов – числу вариантов задаваемых температурных воздействий f.

Элементы матрицы D_t для статически определимой основной системы вычисляются по формуле (17.2). В матричной форме соотношение (17.2) примет вид:

D_t = . (17.6)

L_t – матрица внутренних усилий (изгибающих моментов и продольных сил), необходимых для расчёта сооружения на температурное воздействие в основной системе метода сил от Х₁ = 1, Х₂ = 1, …, Х_j = 1, …, Х_n = 1.

L_t = [L_t1 L_t2 … L_tj … L_tn]; .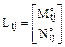

Для k-тых участков, где задано изменение температуры 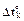= const, элементы блоков 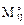и 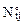фиксируются в срединных сечениях этих участков.

B_t – матрица температурной податливости сооружения.

.

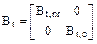B_t,nr – матрица температурной податливости сооружения при неравномерных приращениях температуры; B_t,о – то же при равномерных приращениях температуры. Если для k-го участка a_k = const, h_k = const, то

.

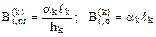Т – матрица приращений температур по вариантам воздействий.

Т = [Т₁ Т₂ … Т_j … Т_f]; .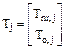

T_nr,j и T_o,j – соответственно, матрицы неравномерных и равномерных приращений температур j-го варианта температурного воздействия. Элементами этих матриц на k-ом участке изменения температуры являются перепады приращений температур по высоте поперечного сечения и приращения температуры в центре тяжести поперечного сечения .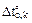

Из системы канонических уравнений (17.5) получим матрицу неизвестных метода сил:

X = –d^-1 D_t. (17.7)

С учётом соотношений (16.21) и (17.6) матричное выражение (17.7) перепишется в развёрнутой форме:

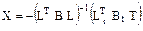. (17.8)

Внутренние усилия M_t, Q_t, N_t в заданном статически неопределимом сооружении от температурного воздействия в матричной форме определим, используя формулы (17.3).

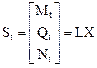. (17.9)

Напоминаем читателям, что L – матрица внутренних усилий, необходимых для получения матрицы коэффициентов при неизвестных метода сил d системы канонических уравнений, в основной системе от X₁ = 1, X₂ = 1, …, X_j = 1, …, X_n = 1. Порядок формирования этой матрицы подробно изложен в п. 16.7 шестнадцатой лекции.

С учётом выражения (17.8) матричное соотношение (17.9) в окончательной форме примет вид:

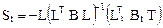. (17.10)

В выражении (17.10) матрица В – это матрица внутренней упругой податливости сооружения. Структура этой матрицы подробно изложена в п. 16.7 шестнадцатой лекции.

Кинематическая проверка правильности расчёта заданного статически неопределимого сооружения на температурное воздействие в матричной форме производится по формуле:

L^T B S_t = –D_t. (17.1)

17.2. Пример расчёта статически неопределимой рамы на температурное воздействие в обычной форме

Со стороны внутренних волокон стержней левого контура рамы (рис. 17.2,а) температура повысилась на 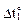= 30 °С, со стороны наружных волокон левой стойки и верхних волокон ригеля температура понизилась на 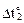= -50 °С. Поперечные сечения элементов рамы прямоугольные размером b´h (h = 0,2 м). Коэффициент линейного температурного расширения материала, из которого изготовлены стержни рамы, известен и равен a. Требуется построить эпюры внутренних усилий от заданного температурного воздействия.

1. Определение степени статической неопределимости рамы:

n_st = 3К – Н = 3 × 2 – 5 = 1.

2. Выбор статически определимой основной системы метода сил. Лишнюю связь заданной рамы удалим путём введения цилиндрического шарнира в её верхний левый узел (рис. 17.2,б). Читателям предлагается произвести кинематический анализ полученной основной системы и убедиться в её геометрической неизменяемости.

3. Построение эпюры изгибающих моментов М₁ и эпюры продольных сил N₁ в основной системе от Х₁ = 1 (рис. 17.2,в).

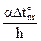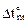4. Построение условных эпюр, связанных с перепадами приращений температур по высоте поперечного сечения и приращениями температур на уровне центров тяжести поперечных сечений (рис. 17.2,г,д). При построении этих эпюр учтено, что h = 0,2 м, и приняты во внимание следующие численные значения величин и :

– для левого ригеля и левой стойки:

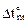= 30 – (–50) = 80 °С, = = 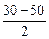–10 °С;

– для правого ригеля:

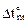= 0 – (–50) = 50 °С, = = 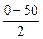–25 °С;

– для правой стойки:

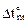= 30 – 0 = 30 °С, = = 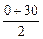15 °С.

Ординаты эпюры 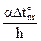отложены со стороны более "тёплых" волокон, на эпюре же aзафиксирован знак "плюс" на элементах с положительными приращениями температур на уровне центров тяжести поперечных сечений и знак "минус" – с отрицательными (см. п. 12.2 и пример 12.2.1 второй части настоящего курса лекций).

5. Вычисление коэффициентов разрешающего уравнения метода сил

d₁₁Х₁ + D_1t = 0. (17.1,а)

Как и при силовом воздействии, в рамных системах коэффициент d₁₁ вычисляется без учёта влияния на величину искомого перемещения деформаций сдвига и растяжения–сжатия.

где .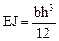

Перемещение по направлению Х₁ от заданного изменения температуры в основной системе определим по формуле (17.2), вычисляя определённые интегралы сопряжением эпюры М₁ с эпюрой 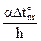и эпюры N₁ с эпюрой a.

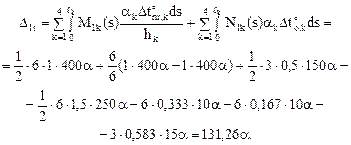
6. Вычисление неизвестного метода сил из уравнения (17.1,а):

7. Определение изгибающих моментов в сечениях заданной рамы от температурного воздействия и построение эпюры M_t (рис. 17.3,а). Из первого выражения соотношений (17.3) имеем:

M_t = M₁ X₁,

где Х₁ = –15aEJ.

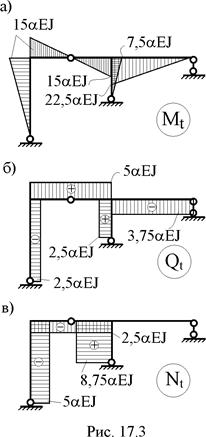
8. Кинематическая проверка решения задачи. Для этой проверки используем формулу (17.4), в которой сохраним только первый член, ибо коэффициент d₁₁ выше нами был определён только с учётом деформаций изгиба.

Результат сопряжения эпюр M_t и М₁ практически совпал с численным значением правой части разрешающего уравнения (17.1,а)

d₁₁ X₁ = –D_1t,

что подтверждает правильность решения поставленной задачи.

9. Построение обычным порядком эпюры поперечных сил Q_t (рис. 17.3,б) и эпюры продольных сил N_t (рис. 17.3,в). В нашей задаче окончательную эпюру продольных сил N_t можно также получить, используя последнее выражение соотношения (17.3), которое для рассматриваемой задачи примет вид:

N_t = N₁ Х₁.

Обращаем внимание читателя на то, что ординаты окончательных эпюр внутренних усилий (М_t, Q_t, N_t) зависят от абсолютного значения изгибной жёсткости поперечного сечения элементов рамы EJ.

17.3. Пример расчёта статически неопределимой рамы на температурное воздействие в матричной форме

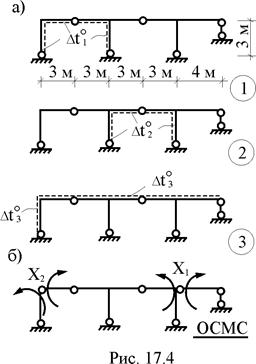В статически неопределимой раме (рис. 17.4,а) возможны следующие независимые друг от друга варианты температурных воздействий: первый – повышение температуры со стороны внутренних волокон стержней левого контура на 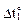= 120 °С, второй – повышение температуры со стороны внутренних волокон элементов среднего контура на 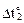= 80 °С, третий – понижение температуры со стороны наружных волокон левой стойки и ригелей на 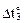= –40 °С. Ширина прямоугольных поперечных сечений стоек и ригелей рамы одинакова и равна b; высота поперечного сечения стойки h_c = h, ригеля – h_p = 1,587h (h = 0,3 м). Коэффициент линейного температурного расширения материала, из которого изготовлены элементы рамы, равен a. Требуется построить эпюры внутренних усилий в заданной раме от каждого из вышеперечисленных вариантов температурных воздействий.

Размеры прямоугольных поперечных сечений рамы заданы так, что сохраняется соотношение изгибных жесткостей поперечных сечений ригелей и стоек, принятое для расчёта этой же рамы, в матричной форме на силовое воздействие в п. 16.8 шестнадцатой лекции, а именно: EJ_p: EJ_c = 2: 0,5. Приняв EJ_p = 2 EJ, EJ_с = 0,5 EJ, получим численное значение жесткостного параметра EJ:

.

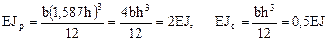Каждое из этих соотношений даёт

.

Для расчёта рамы на температурное воздействие в матричной форме используем соотношение (17.10), в котором примем L = M, B = B_M, S_t = M_t, так как вычисление матрицы внешней жёсткости принятой основной системы метода сил (рис. 17.4,б) будем производить только с учётом изгибных деформаций. В этом случае матричное выражение (17.10) перепишется:

M_t = –M(M^T B_M M)^-1 (L^T_t B_t T).

1. Определение степени статической неопределимости рамы и выбор основной системы метода сил (рис. 17.4,б). Основная система для расчёта рамы на температурное воздействие будет такой же, как и при её расчёте на силовое воздействие в матричной форме (см. п. 16.8 шестнадцатой лекции).

2. Построение эпюр изгибающих моментов и продольных сил в основной системе метода сил от Х₁ = 1 и Х₂ = 1 (рис. 17.5,а). Эпюры изгибающих моментов М₁ и М₂ от этих воздействий были получены ранее (см. п. 16.8, рис. 16.14,в,г).

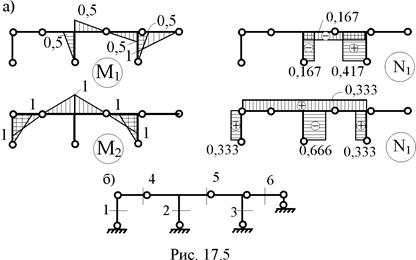
3. Формирование матрицы изгибающих моментов М от Х₁ = 1 и Х₂ = 1 в основной системе и матрицы внутренней упругой податливости В_М в соответствии с принятой на рис. 16.16 нумерацией грузовых участков и сечений (см. п. 16.8 шестнадцатой лекции).

5. Вычисление элементов матрицы внешней податливости принятой для расчёта основной системы метода сил (см. п. 16.8 шестнадцатой лекции).

.

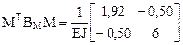6. Обращение матрицы внешней податливости рамы (см. п. 16.8 шестнадцатой лекции).

.

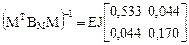7. Нумерация участков и сечений для формирования матрицы изгибающих моментов и продольных сил от Х₁ = 1, Х₂ = 1 в основной системе L_t, матрицы температурной податливости сооружения B_t и матрицы приращений температур Т (рис. 17.5,б). Заметим, что при расчёте рамы на температурное воздействие номера участков и их срединных сечений совпадают.

8. Формирование матрицы L_t по эпюрам внутренних усилий M₁, N₁, M₂, N₂ (рис. 17.5,а) в соответствии с принятой нумерацией срединных сечений.

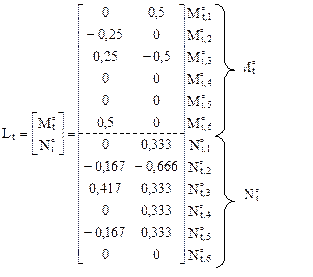
9. Формирование матрицы температурной податливости сооружения B­_t в соответствии с принятой нумерацией участков (рис. 17.5,б).

,

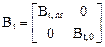где ,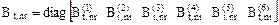

;

.

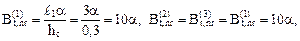
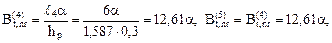
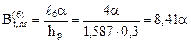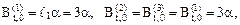
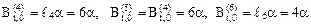10. Построение эпюр неравномерных (T_nr) и равномерных приращений температур (Т₀) по вариантам воздействий (рис. 17.6).

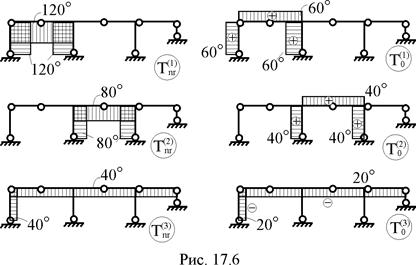
Ординатами этих эпюр (соответственно, и элементами матриц T_nr и T₀) на k-том участке являются перепад приращений температур по высоте поперечного сечения и приращение температуры в центре тяжести поперечного сечения 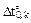. Численное значение величин и 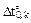по вариантам воздействий читателям предлагается получить самостоятельно.

11. Формирование матрицы приращений температур Т по вариантам воздействий (рис. 17.6) в соответствии с принятой нумерацией участков. Правило знаков для элементов матрицы T_nr совпадает с правилом знаков для элементов матрицы М (см. пример 13.4.1 тринадцатой лекции). Знаки элементов подматрицы Т₀ совпадает со знаком приращений температуры в центрах тяжести поперечных сечений 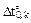, т.е. со знаками эпюры Т₀ на рассматриваемых участках.

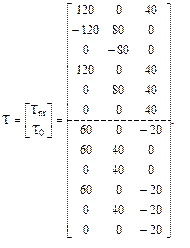
12. Вычисление элементов матрицы свободных членов системы канонических уравнений по вариантам воздействий

.

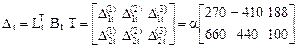13. Определение матрицы неизвестных метода сил по вариантам температурных воздействий.

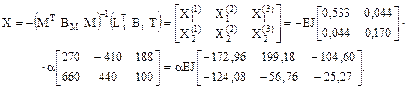
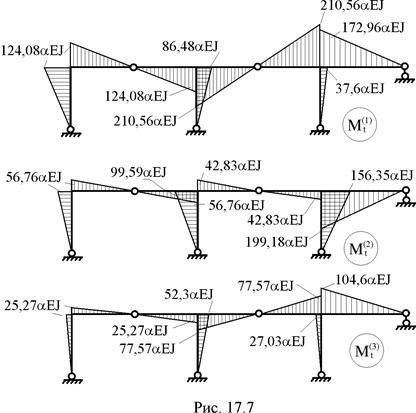
14. Вычисление элементов матрицы изгибающих моментов M_t в заданной раме и построение соответствующих эпюр по вариантам температурных воздействий (рис. 17.7) в соответствии с принятой нумерацией участков и сечений (рис. 16.16).

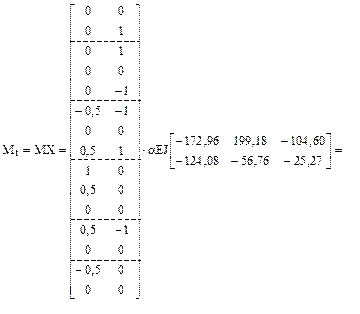
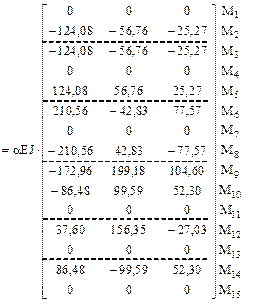
15. Кинематическая проверка. Используя матричное соотношение (17.11), в котором для нашей задачи L = M, B = B_M, S_t = M_t, мы должны получить матрицу свободных членов системы канонических уравнений по вариантам температурных воздействий с обратным знаком, т.е.

M^T B_M M_t = –D_t.

После подстановки в последнее соотношение матриц М, В_М и M_t получим:

M^T B_M M_t = .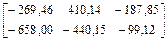

Элементы вычисленной матрицы по абсолютной величине соответствуют элементам матрицы D_t, полученной выше, с относительной погрешностью, не превышающей 0,9 %.

16. Построение по вариантам температурных воздействий эпюр поперечных сил Q_t по эпюрам М_t и эпюр продольных сил N_t по эпюрам Q_t. Читателям предлагается построение этих эпюр выполнить самостоятельно.

17.4. Расчёт стержневых статически неопределимых систем на кинематическое воздействие

В плоской стержневой системе, степень статической неопределимости которой равна n, имеет место n независимых друг от друга кинематических возмущений, например, смещений линейных и угловых опорных связей (рис. 17.8,а). Жесткостные характеристики поперечных сечений элементов системы любого k-го участка на изгиб EJ_k, сдвиг GA_k и растяжение–сжатие EA_k примем постоянными.

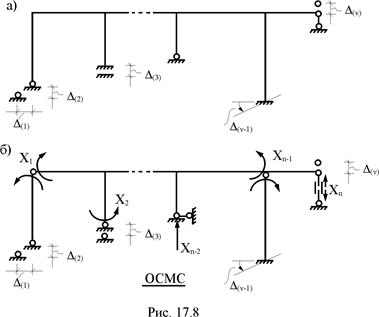
Удаляя из заданного сооружения n лишних связей (рис. 17.8,б), образуем статически определимую основную систему метода сил (ОСМС). Особое внимание при выборе основной системы следует обращать на удаление связей, получивших в рассчитываемом сооружении перемещение. В частности, при наличии кинематического возмущения линейной связи её отбрасывание недопустимо, так как в этом случае из расчётной схемы основной системы исключается связь с диском "земля", являющимся причиной рассматриваемого линейного смещения по направлению опорной связи. В этом случае в произвольное сечение смещаемой опорной связи вводится поступательный шарнир (рис. 17.8,б – правая вертикальная опора).

Неизвестные метода сил X₁, X₂, …, X_j, …, X_n определим из условий равенства нулю перемещений по направлениям X_i (i = 1, 2, …, n) в основной системе метода сил от неизвестных этого метода и заданного смещения связей. Повторяя выкладки, приведённые в п. 16.2 шестнадцатой лекции, получим систему канонических уравнений для определения неизвестных метода сил в случае кинематического воздействия на сооружение. Строка i этой системы уравнений имеет вид:

d_i1X₁ + d_i2X₂ + … + d_iiX_i + … + d_ijX_j + … + d_inX_n + D_ic = 0. (17.12)

Главные d_ii и побочные d_ij коэффициенты системы канонических уравнений определяются по формулам (16.5)–(16.6) в общем случае плоских стержневых систем и формулам (16.8)–(16.9) для рам и балок (см. п. 16.2 шестнадцатой лекции).

Свободный член j-й строки системы канонических уравнений D_ic есть перемещение по направлению усилия X_i в i-й удалённой лишней связи в основной системе метода сил от заданного кинематического возмущения. В статически определимой основной системе, принятой для расчёта, указанное перемещение определяется по формуле (12.6), полученной в п. 12.3 второй части настоящего курса лекций:

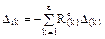. (17.13)

В формуле (17.13) 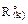– реакция в k-й связи, получившей кинематическое воздействие, от X_i = 1 в статически определимой основной системе; D_(k) – величина кинематического воздействия, например, смещения k-й опорной связи.

Как и при температурном воздействии, значения жесткостных характеристик поперечных сечений элементов сооружения EJ_k, GA_k, EA_k не входят в соотношение (17.13). Это значит, что численные значения усилий в лишних связях и, следовательно, внутренних усилий в заданном сооружении, есть функции абсолютных значений жесткостей поперечных сечений стержней.

Вычислив из системы канонических уравнений усилия в лишних связях, мы расчёт статически неопределимого сооружения на кинематическое воздействие (рис. 17.8,а) свели к расчёту статически определимой основной системы метода сил (рис. 17.8,б). Так как кинематическое воздействие в статически определимых сооружениях внутренних усилий не вызывает (см. п. 12.1 второй части настоящего курса лекций), то величины изгибающих моментов М_с, поперечных Q_c и продольных сил N_c в сечениях заданного сооружения в этом случае определяются только усилиями в лишних связях X₁, X₂, …, X_j, …, X_n. Имея эпюры внутренних усилий M_j, Q_j, N_j от Х_j = 1 в основной системе и применяя принцип независимости действия сил, получим:

M_с = M₁X₁ + M₂X₂ + … + M_jX_j + … + M_nX_n,

Q_с = Q₁X₁ + Q₂X₂ + … + Q_jX_j + … + Q_nX_n, (17.14)

N_с = N₁X₁ + N₂X₂ + … + N_jX_j + … + N_nX_n.

Эпюры внутренних усилий M_с, Q_с, N_с в заданном сооружении должны удовлетворять кинематическим условиям, а именно: перемещения по направлению любых усилий X­_i­ (i = 1, 2, …, n) в отброшенных связях в основной системе метода сил от действия всех упомянутых усилий X₁, X₂, …, X_j, …, X_n и от заданного кинематического возмущения должны быть равны нулю. Другими словами, численные значения перемещений по направлению X_i в статически определимой основной системе от всех неизвестных метода сил будут равны величинам перемещений, вызываемых кинематическим воздействием, с обратным знаком, т.е.

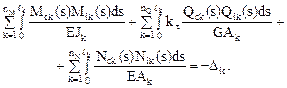(17.15)

Соотношение (17.15) по смыслу аналогично формуле (17.4), полученной в п. 17.1 для случая температурного воздействия на сооружение.

В матричной форме система канонических уравнений метода сил при кинематическом воздействии запишется:

dХ + D_с = 0. (17.16)

d – матрица внешней податливости принятой для расчёта заданного сооружения основной системы метода сил. Для вычисления её элементов используется матричное соотношение (16.21), полученное в п. 16.7 шестнадцатой лекции.

Х и D_с – соответственно, матрицы неизвестных метода сил и перемещений по направлению этих неизвестных от заданного кинематического воздействия в основной системе. Число строк в матрицах Х и D_с равно степени статической неопределимости сооружения, а число столбцов – числу вариантов кинематических возмущений.

В матричной форме соотношение (17.13) для вычисления элементов матрицы D_с запишется:

D_с = 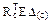. (17.17)

R_c – матрица реакций в связях, получивших кинематическое возмущение, от X₁ = 1, X₂ = 1, …, X_j = 1, …, X_n = 1 в статически определимой основной системе метода сил.

R_c = [R_c1 R_c2 … R_cj … R_cn].

D_(с) – матрица величин заданных кинематических возмущений по вариантам воздействий.

D_(с) = .

Число строк в матрицах R_c и D_(с) равно e – суммарному числу кинематических возмущений во всех вариантах воздействий; число столбцов: в матрице R_c – степени статической неопределимости сооружения n, в матрице D_(с) – числу вариантов кинематических воздействий n.

Е – единичная матрица порядка e´e, элементы которой учитывают знак "минус" формулы (17.13), т.е. отрицательны.

Е = diag [-1 -1 … -1 -1].

Матрицу неизвестных метода сил получим из системы канонических уравнений (17.16):

Х = –d^-1D_с. (17.18)

В развёрнутой форме соотношение (17.18) с учётом матричных выражений (16.21) и (17.17) перепишется:

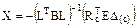. (17.19)

Напоминаем, порядок формирования матиц L и В изложен в п. 16.7 шестнадцатой лекции.

Внутренние усилия M_c, Q_c, N_c в заданном статически неопределимом сооружении от кинематического воздействия в матричной форме определим, используя соотношения (17.14).

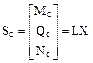. (17.20)

Матричное выражение (17.20) с учётом соотношения (17.19) в окончательной форме примет вид:

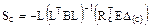. (17.21)

Кинематическая проверка правильности вычисления элементов матрицы S_c производится с помощью следующей матричной формулы:

L^T B S­_c = –D_c. (17.22)

17.5. Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

В раме, показанной на рис. 17.9,а, горизонтальная связь левой опоры получила перемещение влево на D₍₁₎ = 2 см, вертикальная связь этой же опоры – вниз на D₍₂₎ = 1 см. Изгибная жёсткость поперечных сечений стержней рамы известна и равна постоянной величине EJ. Требуется построить эпюры внутренних усилий от заданного смещения опорных связей.

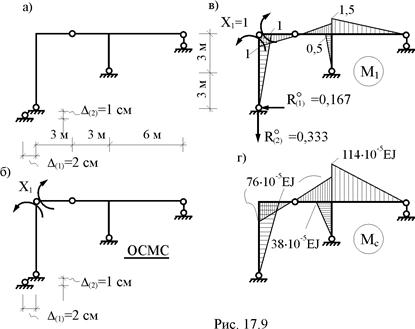
В п. 17.2 эта же рама была рассчитана на температурное воздействие. Некоторыми результатами этого расчета воспользуемся в рассматриваемом примере.

1. Определение степени статической неопределимости и выбор статически определимой основной системы метода сил (см. п. 17.2, рис. 17.9,б).

2. Построение эпюры изгибающих моментов М₁ и вычисление реакций в смещаемых связях 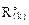в основной системе от Х₁ = 1 (рис. 17.9,в).

3. Вычисление коэффициентов разрешающего уравнения метода сил

d₁₁ Х₁ + D_1с = 0.

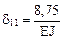(см. п. 17.2).

Перемещение по направлению Х₁ от заданного смещения опорных связей определим по формуле (17.13).

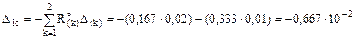(рад).

4. Решение уравнения метода сил:

.

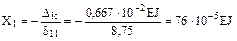5. Определение изгибающих моментов в характерных сечениях рамы от заданных смещений горизонтальной и вертикальной связей левой опоры и построение эпюры М_с (рис. 17.9,г). Из первого выражения группы соотношений (17.14) следует:

M_c = M₁X₁, где X₁ = 76 × 10^-5EJ.

6. Кинематическая проверка эпюры М_с по формуле (17.15). В этой формуле сохраним только первый член, учитывающий изгибные деформации элементов рамы.

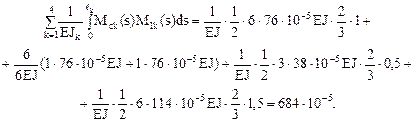
Результат сопряжения эпюр М_с и М₁ совпадает с численным значением правой части разрешающего уравнения метода сил d₁₁Х₁ = –D_1с = –(-0,667×10^-2) = 667×10^-5 с относительной погрешностью вычислений:

e = 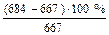= 2,55 %,

что подтверждает правильность вычисления ординат эпюры М_с.

7. Построение эпюры поперечных сил Q_c по эпюре изгибающих моментов М_с и эпюры продольных сил N_c по эпюре Q_c. Читателям предлагается самостоятельно выполнить построение эпюр Q_c и N_c.

17.6. Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

В раме, показанной на рис. 17.10, возможны следующие независимые друг от друга кинематические воздействия: первое – перемещение вертикальной связи левой опоры вниз на D₍₁₎ = 2 см, второе – перемещение горизонтальной связи вправо на D₍₂₎ = 1,5 см и вертикальной вверх на D₍₃₎ = 1 см опоры центральной стойки, третье – перемещение правой опоры вверх на D₍₄₎ = 3 см. Численные значения изгибных жесткостей поперечных сечений ригеля EJ_p и стоек EJ_с рамы заданы: EJ_p = 2 EJ, EJ_с = 0,5 EJ (EJ – известное число). Требуется вычислить элементы матрицы изгибающих моментов М_с для характерных сечений заданной рамы от каждого из вышеперечисленных кинематических воздействий.

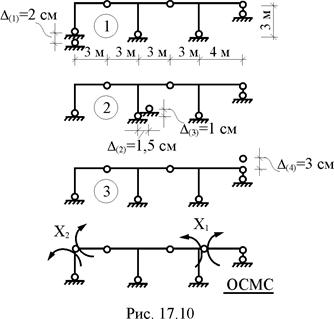
Для расчёта рамы в матричной форме с учётом только изгибных деформаций её элементов используем соотношение (17.21). В этом случае L = М, В = В_М, S_c = M_c и матричное выражение (17.21) примет вид:

.

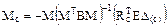В дальнейшем воспользуемся некоторыми результатами расчёта этой же рамы на силовое воздействие (см. п. 16.8 шестнадцатой лекции).

1. Выбор основной системы метода сил (рис. 16.14,б, рис. 17.10), построение в ней эпюр изгибающих моментов от Х₁ = 1, Х₂ = 1 (рис. 16.14,в,г), нумерация участков и сечений (рис. 16.16), формирование матриц изгибающих моментов в основной системе от Х₁ = 1, Х₂ = 1 и внутренней упругой податливости рамы М и В_М, вычисление элементов матрицы внешней податливости d = М^Т В_М М, обращение этой матрицы.

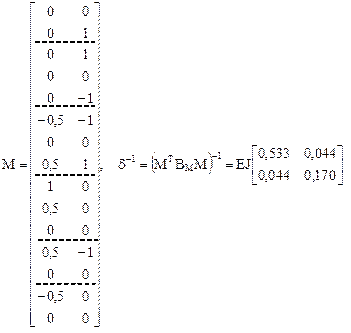
Примечание. Для расчёта рамы на температурное воздействие (см. п. 17.3) и в настоящем примере количество сечений на грузовых участках ригеля сохранено таким же, как и при расчёте рамы на силовое воздействие (рис. 16.16). Это обусловлено тем, что расчёт статически неопределимых систем на температурные и кинематические воздействия с помощью вычислительной техники производится вместе с расчётом на силовое воздействие. В частности, на кафедре строительной механике НГАСУ для расчёта статически неопределимых систем методом сил на все виды независимых друг от друга воздействий (силовые, температурные и кинематические) используется программа "Mefor", разработанная профессором В.Г. Себешевым.

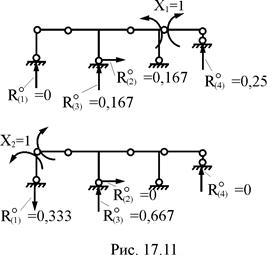
2. Формирование матрицы реакций в связях, получивших перемещение, от Х₁ = 1, Х₂ = 1 в основной системе (рис. 17.11).

.

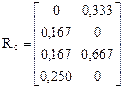В первой строке этой матрицы сначала от Х₁ = 1 (первый столбец), затем от Х₂ = 1 (второй столбец), зафиксированы реакции вертикальной связи левой опоры, во второй – реакции горизонтальной связи опоры центральной стойки, в третьей – вертикальной связи опоры центральной стойки, в четвёртой – правой опорной связи. Напоминаем, что реакция в смещаемой связи вносится в матрицу R_c со знаком "плюс", если её направление совпадает с направлением смещения связи, и со знаком "минус", – если не совпадает.

3. Составление матрицы величин перемещений опорных связей (в м) по вариантам воздействий.

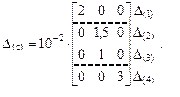
4. Вычисление матрицы перемещений по направлениям Х₁ и Х₂ от заданных кинематических возмущений в основной системе, или матрицы свободных членов системы канонических уравнений (17.16).

D_с = =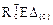

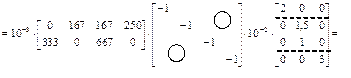
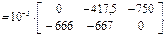
5. Определение элементов матрицы неизвестных метода сил.

X = –d^-1D_c = –(M^T B_M M)^-1 (R_c E D­_(c)) =

=

.

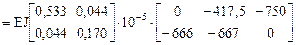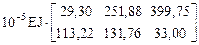6. Получение матрицы изгибающих моментов М_с в заданной раме по вариантам кинематических воздействий (рис. 17.10) в соответствии с принятой нумерацией участков и сечений (рис. 16.16).

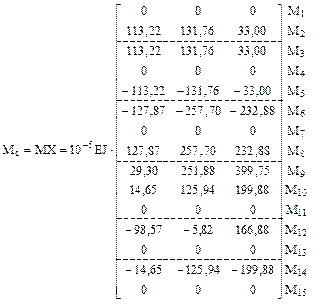
Читателям предлагается (используя соотношение (17.22), самостоятельно произвести кинематическую проверку правильности вычисления элементов матрицы М_с и построить для заданной рамы сначала эпюры изгибающих моментов, а затем и эпюры поперечных и продольных сил от упомянутых выше смещений опорных связей.

Дата добавления: 2014-01-15