
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад. Розв’язати рівняння
|
|
|
|
Приклад. Розв’язати рівняння
 .
.
Ø Винісши корінь четвертого степеня за дужки і виконавши відповідні перетворення, дістанемо:
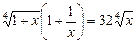 ,
, 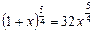 ,
, 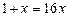 ,
, 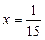 .
.
 .
.
Ø Виносимо 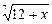 за дужки і виконуємо перетворення:
за дужки і виконуємо перетворення:
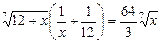 ,
, 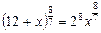 .
.
Остаточно маємо:
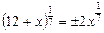 ,
,  ,
, 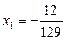 ,
, 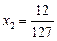 .
.
5.8. Рівняння з кубічними ірраціональностями
Розглянемо ірраціональне рівняння виду
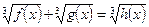 . (1)
. (1)
Піднесемо обидві частини рівняння до куба:
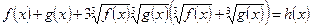 .
.
Спростимо здобуту рівність, скориставшись (1):
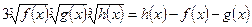 . (2)
. (2)
Підносимо обидві частини рівняння (2) до куба:
 .
.
Якщо рівняння (1) має корінь, то він є і коренем рівняння (2). Проте рівняння (2) може мати корінь, який не є коренем рівняння (1).
Позначимо 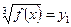 ,
, 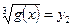 ,
, 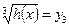 .
.
Тоді рівняння (2) набере вигляду
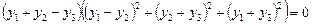 .
.
Це рівняння відрізняється від рівняння (1), яке, скориставшись тими самими позначеннями, можна записати у вигляді  . Якщо рівняння (2) має корені, які не задовольняють рівняння (1), тобто сторонні щодо нього, то вони є коренями таких рівнянь:
. Якщо рівняння (2) має корені, які не задовольняють рівняння (1), тобто сторонні щодо нього, то вони є коренями таких рівнянь:
 ,
, 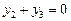 ,
, 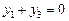 ,
,
або, у початкових позначеннях:
 ;
; 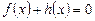 ,
,  . (3)
. (3)
Отже, якщо при рішенні розв’язуванні (2) з’явилися сторонні корені, то вони задовольняють систему рівнянь (3).
Приклад. Розв’язати рівняння
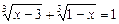 .
.
Ø Підносимо обидві частини рівняння до куба і виконуємо відповідні перетворення
 ;
;  .
.
Остаточно маємо: 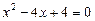 ,
,  .
.
Цей корінь не задовольняє дане рівняння, але є коренем системи рівнянь виду (3):
 ;
; 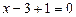 ,
,  .
.
Приклад. Розв’язати рівняння
 .
.
Ø Підносимо рівняння до куба за формулою (2):
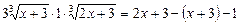 ,
,
 ;
; 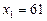 ;
;  .
.
Корінь  не задовольняє рівняння, але задовольняє систему рівнянь:
не задовольняє рівняння, але задовольняє систему рівнянь:
 ;
;  ;
;  .
.
Приклад. Розв’язати рівняння
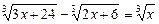 .
.
Ø За формулою (2) знаходимо:
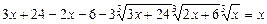 ,
,
 ,
, 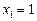 ,
,  .
.
Перевірка показує, що корінь  — сторонній.
— сторонній.
5.9. Заміна радикалів новими невідомими
Основним способом розв’язування складних ірраціональних рівнянь є заміна кожного радикала новим невідомим. Це дає змогу звести ірраціональне рівняння до системи алгебраїчних рівнянь.
|
|
|
Приклад. Розв’язати рівняння
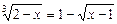 .
.
Ø Позначивши
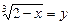 ,
,  ,
,
дістанемо систему алгебраїчних рівнянь

Передусім виключаємо невідоме 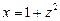 :
:
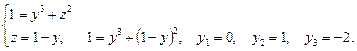
Звідси знаходимо розв’язки  ,
,  ,
, 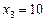 .
.
Приклад. Розв’язати рівняння
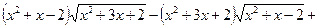
 .
.
Ø Позначимо радикали:

Рівняння зводиться до системи рівнянь:
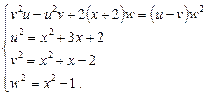
Насамперед виключаємо невідоме  :
:
 .
.
Дістанемо рівняння
 ,
,
яке розкладається на множники:
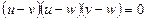 .
.
Розв’язуємо рівняння:
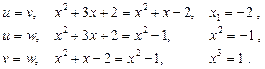
Корінь  не задовольняє рівняння.
не задовольняє рівняння.
Приклад. Розв’язати рівняння
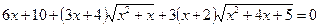 .
.
Ø Уводимо позначення:

Рівняння зводиться до системи рівнянь

Розкладаємо перше рівняння на множники:
 .
.
Розв’язуємо рівняння:
1)  ;
;
2) 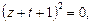
 ,
, 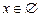 .
.
5.10. Уведення параметра
Ірраціональні рівняння так само, як алгебраїчні, можна розв’язувати ввведенням допоміжного параметра [2], що значно спрощує розв’язування.
Приклад. Розв’язати рівняння
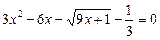 .
.
Ø Запишемо рівняння у вигляді
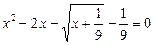 .
.
Заміна  зводить рівняння до вигляду
зводить рівняння до вигляду
 .
.
Уводимо параметр 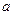 , вважаючи
, вважаючи  .
.
Дістанемо ірраціональне рівняння з параметром:
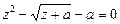 ,
,  .
.
Маємо квадратне рівняння відносно 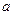 :
:
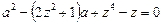 .
.
Знаходимо розв’язки:
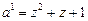 ,
, 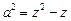 .
.
Для відшукання  розв’язуємо такі рівняння:
розв’язуємо такі рівняння:
 ,
, 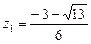 ,
, 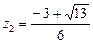 ;
;
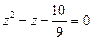 ,
, 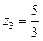 ,
,  .
.
Звідси знаходимо значення  :
:
 ,
, 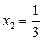 ,
,  ,
, 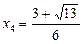 .
.
Корені 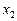 ,
, 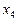 — сторонні.
— сторонні.
Приклад. Розв’язати рівняння
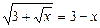 .
.
Ø Уводимо параметр  . Дістаємо рівняння
. Дістаємо рівняння
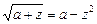 ,
,  .
.
Звільняючись від ірраціональності, маємо:
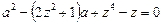 ,
,
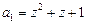 ,
,  .
.
Підставляючи значення  , дістаємо:
, дістаємо:
 ,
, 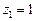 ,
, 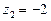 ;
;
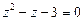 ,
,  ,
,  .
.
Задовольняють рівняння лише корені  .
.
Приклад. Розв’язати рівняння
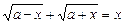 .
.
Ø Знаходимо ОДЗ:

Підносимо обидві частини рівняння до квадрата:
 ;
;
 ;
; 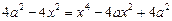 ;
;
 ,
, 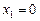 ,
,  ,
, 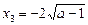 .
.
Корінь 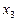 не входить в ОДЗ. Якщо
не входить в ОДЗ. Якщо 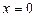 , то
, то 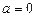 . Знайдемо значення
. Знайдемо значення 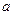 , при яких маємо корінь
, при яких маємо корінь 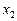 . Підставимо
. Підставимо 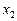 у вихідне рівняння
у вихідне рівняння
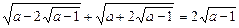 ;
;
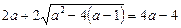 ,
,  ;
; 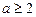 .
.
Остаточно маємо: 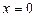 при
при 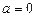 ;
; 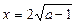 при
при 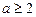 .
.
5.11. Рівняння з модулями
Рівняння з модулями близькі до ірраціональних рівнянь, оскільки
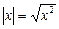 . (1)
. (1)
Звичайно використовують означення модуля х:
|
|
|
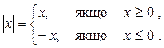
Приклад. Розв’язати рівняння
 .
.
Ø Згідно з умовою  дістаємо рівняння
дістаємо рівняння  . Якщо
. Якщо 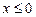 , то
, то 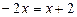 ,
, 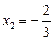 .
.
Приклад. Розв’язати рівняння
 .
.
Ø Знайдемо точки, в яких модулі перетворюються на нуль:
 ,
, 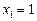 ;
; 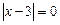 ,
,  .
.
Ці точки розбивають числову вісь на частини, в кожній з яких вирази під знаком модуля мають один і той самий знак.
1)  ;
;  ,
, 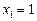 ;
;
2)  ;
; 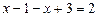 ,
,  — маємо тотожності;
— маємо тотожності;
3) 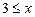 ;
;  ,
,  .
.
Остаточно дістаємо  .
.
Приклад. Розв’язати рівняння
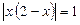 .
.
Знайдемо точки, де 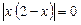 ,
, 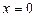 ,
,  . Розглянемо всі можливі випадки:
. Розглянемо всі можливі випадки:
1) 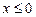 ,
,  ,
, 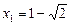 ;
;
2) 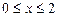 ;
; 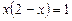 ,
,  ;
;
3)  ;
;  ,
,  .
.
Приклад. Розв’язати систему рівнянь

Ø Розглянемо всі можливі випадки.
1)  ,
, 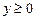 :
:
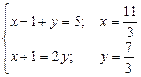 . Знайшли розв’язок системи.
. Знайшли розв’язок системи.
2)  ,
, 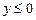 :
:
 . Розв’язок не задовольняє умову.
. Розв’язок не задовольняє умову.
3)  ,
, 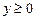
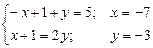 . Розв’язок не задовольняє умову.
. Розв’язок не задовольняє умову.
4)  ,
, 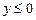
 . Знайшли розв’язок системи. ×
. Знайшли розв’язок системи. ×
З формули (1) випливають правила внесення (винесення) множників під знак радикала:
 . (2)
. (2)
Якщо множник 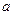 вноситься під радикал, то знак множника
вноситься під радикал, то знак множника 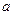 залишається поза радикалом.
залишається поза радикалом.
Приклад. Розв’язати рівняння
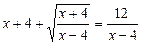 .
.
Ø Помножимо обидві частини рівняння на  ,
, 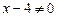 .
.
 .
.
Розглянемо можливі випадки.
1. 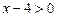 . Вносимо додатний множник під знак радикала:
. Вносимо додатний множник під знак радикала:
 ,
, 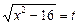 ,
,  ,
,
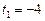 ,
,  .
. 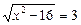 ;
;  ,
, 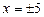 .
.
Корінь  не задовольняє умові. Остаточно маємо
не задовольняє умові. Остаточно маємо 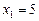 .
.
2. 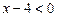 . Вносимо від’ємний множник під знак радикала за формулою (2):
. Вносимо від’ємний множник під знак радикала за формулою (2):
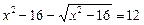 ,
, 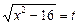 ,
,  ,
, 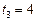 ,
,  .
.
 ,
, 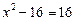 ,
, 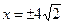 . Корінь
. Корінь  не задовольняє умову. Остаточно маємо:
не задовольняє умову. Остаточно маємо:  .
.
5.12. Системи ірраціональних рівнянь
Системи двох ірраціональних рівнянь дуже різноманітні, і тому важко знайти загальні способи їх розв’язування. Зазвичай намагаються виключити одне невідоме й дістати одне рівняння з одним невідомим.
Приклад. Розв’язати систему рівнянь

Ø Позначимо  ,
, 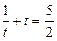 ,
,  ,
, 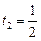 .
.
Із системи рівнянь знаходимо
1)  ,
,  ,
, 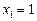 ,
, 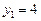 ;
;
2)  ,
,  ,
,  ,
,  .
.
Приклад. Розв’язати систему рівнянь
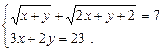
Ø Позначивши  ,
,  , дістанемо систему рівнянь:
, дістанемо систему рівнянь:
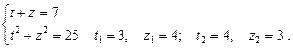
Розв’язуємо системи рівнянь:
1) 

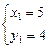 ;
;
2) 
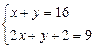
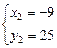 .
.
Приклад. Розв’язати систему рівнянь
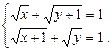
Ø Підносимо обидві частини кожного рівняння до квадрата:
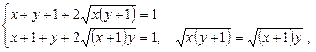
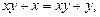
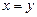 .
.
Розв’язуємо рівняння:
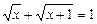 ,
, 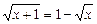 ,
, 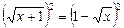 ,
,
 ,
,  ,
, 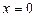 ,
, 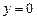 .
.

1. Як знаходять ОДЗ?
2. Як розв’язати рівняння з кубічними ірраціональностями?
3. У чому полягає заміна радикалів новими невідомими?
4. Як розв’язати рівняння з модулями?
5. Як розв’язати однорідне рівняння?

Розв’язати рівняння на ОДЗ (1 — 6). Відповідь
1.  . – 6
. – 6
2. 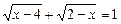 . Æ
. Æ
3. 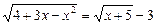 . 4
. 4
4.  . 1
. 1
5. 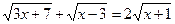 . 3
. 3
6.  . Æ
. Æ
Піднесення обох частин рівняння до квадрата (7—11)
7.  . – 1
. – 1
|
|
|
8. 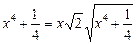 .
. 
9.  .
. 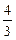
10.  .
. 
11.  . 3
. 3
Метод заміни (12—26)
12. 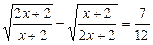 . 7
. 7
13.  .
. 
14. 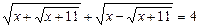 . 5
. 5
15. 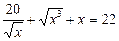 . 1; 4
. 1; 4
16. 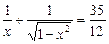 . Æ
. Æ
17.  .
. 
18.  . – 1
. – 1
19.  . – 7; 2
. – 7; 2
20.  . 1
. 1
21. 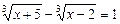 . –6; 3
. –6; 3
22. 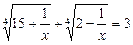 . 1
. 1
23. 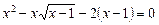 . 2
. 2
24.  . 27
. 27
25.  . 2; 3
. 2; 3
26.  . 4
. 4
Виділення повного квадрата (27—35)
27. 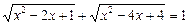 .
. 
28.  . –2; 0
. –2; 0
29.  . Æ
. Æ
30. 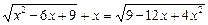 .
. 
31. 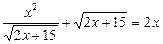 . 5
. 5
32.  .
. 
33. 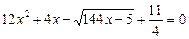 .
. 
34.  .
. 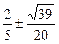
35. 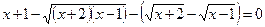 . 2
. 2
Множення на спряжений вираз (36—40)
36.  .
. 
37.  .
. 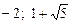
38.  . Æ
. Æ
39.  .
. 
40. 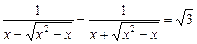 . 4
. 4
Розв’язати різні ірраціональні рівняння (41—75)
41.  . – 1
. – 1
42.  .
. 
43.  . – 2; –1; 2
. – 2; –1; 2
44. 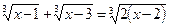 . 1; 2; 3
. 1; 2; 3
45.  . 6
. 6
46.  .
. 
47. 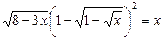 .
. 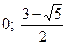
48.  .
. 
49. 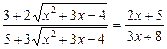 . 5
. 5
50.  .
. 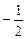
51.  . 3
. 3
52.  . 1
. 1
53.  . 2; 9
. 2; 9
54.  . 2
. 2
55. 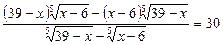 . 7; 38
. 7; 38
56.  .
. 
57.  . 7
. 7
58. 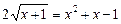 .
. 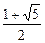
59.  .
. 
60.  .
. 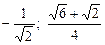
61. 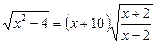 . – 2; – 4
. – 2; – 4
62.  .
. 
63.  . 1
. 1
64. 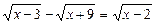 . Æ
. Æ
65.  . Æ
. Æ
66.  . 31
. 31
67. 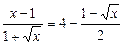 . 81
. 81
68.  . 0; 7
. 0; 7
69.  . – 3,2; 3
. – 3,2; 3
70. 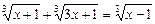 . – 1
. – 1
71. 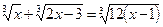 . – 1; – 3
. – 1; – 3
72.  . 3; – 24; – 88
. 3; – 24; – 88
73.  . 1; 2; 10
. 1; 2; 10
74. 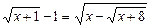 . 8
. 8
75.  . 3
. 3
Розв’язати систему рівнянь (76 — 90)
76. 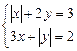 .
. 
77. 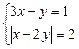 .
. 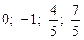
78.  . 6; 10; 10; 6
. 6; 10; 10; 6
79.  . 1; 4; 4; 1
. 1; 4; 4; 1
80. 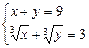 . 1; 8; 8; 1
. 1; 8; 8; 1
81.  .
. 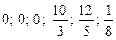
82. 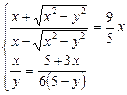 . 5; 3
. 5; 3
83.  . 5; 4
. 5; 4
84. 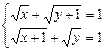 . 0; 0
. 0; 0
85. 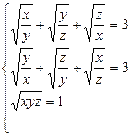 . 1; 1; 1
. 1; 1; 1
86.  . 5; 3; 5; 4
. 5; 3; 5; 4
87. 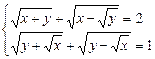 .
. 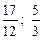
88. 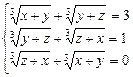 . – 4; 5; 3
. – 4; 5; 3
89.  . 4; 1; 1; 4; – 4; – 1; – 1; – 4
. 4; 1; 1; 4; – 4; – 1; – 1; – 4
90.  . 11; 1
. 11; 1
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1792; Нарушение авторских прав?; Мы поможем в написании вашей работы!