Лекция №1. В результате выполнения данной лабораторной работы были рассмотрены основы топологического анализа систем

АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ

Вывод

В результате выполнения данной лабораторной работы были рассмотрены основы топологического анализа систем, метод матричного вычисления вероятности связного графа. Написана программа для вычисления вероятностей отказа систем распределенной обработки данных при распределениях типа «дерево», «шина», «кольцо», «сеть». Результаты показали, что наибольшую устойчивость имеют системы топологий «дерево» и «шина», а наименее устойчива система с топологией «кольцо».

Введение. Дифференциальные уравнения с частными производными второго порядка. Постановка задачи Коши

и краевых задач. Корректные и некорректные краевые задачи. Методы решения. Метод Фурье (общая схема). Уравнения теплопроводности. Фундаментальное решение.

Интеграл (формула) Пуассона для задачи Коши

Введение. Дифференциальные уравнения с частными производными

2-го порядка.

Разработка и расчет новых изделий, аппаратов, конструкций или технологических процессов осуществляются на основе законов физики, механики, химии и т.д., которые обычно формулируются в виде дифференциальных уравнений (уравнения, содержащие производные от некоторых величин). Многие, практически важные задачи гидроаэромеханики, тепло - массопереноса, теплопроводности, диффузии, теории упругости и прочности и др. областей знаний описываются дифференциальными уравнениями в частных производных, в частности, уравнениями 2-го порядка.

Таким образом, в сущности, любая задача проектирования, связанная с расчетом потоков энергии, вещества, движения тел, или каких-либо конструкций, деталей, в конечном счете, сводится к решению дифференциальных уравнений.

Например, при расчете строительных конструкций, деталей машин, элементов зданий и т.п. необходимо определить степени их надежности

(способность элемента объекта (системы) функционировать в заданных пределах изменения параметров, характеризующих состояние системы). Обычно устанавливаются границы деформации и напряжения, т.е. проводится расчет на прочность, жесткость и устойчивость элементов конструкции. При этом их допустимые значения задаются (устанавливаются)

реальные значения определяются на основании расчетов по математической или физической модели объекта (решаются дифф. уравнения).

Реальные значения должны быть допустимых. Например:

1) Расчет напряженно-деформированного состояния.

Напряженно-деформированное состояние твердых тел описывается уравнением равновесия:

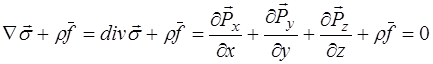(1)

(1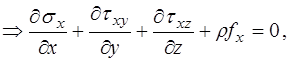.1´)

(1.2´) (1´)

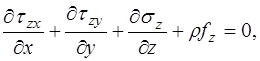(1.3´)

где компоненты тензора напряжений выражаются через компоненты тензора деформации определяющими соотношениями (реологическое уравнение состояния): в случае линейной теории упругости законом Гука для изотропных тел:

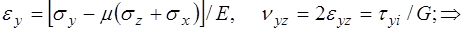
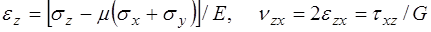
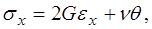
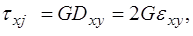
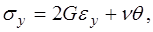
(1´´)

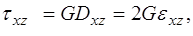
Здесь 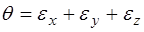, G- модуль сдвига,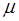- коэффициент Пуассона (поперечного деформирования: 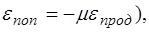Е – модуль Юнга (продольной упругости ); -постоянная Ляме; - плотность массовых сил; Уравнения (1´)-(1´´) решаются при соответствующих граничных условиях по перемещениям (геометрические условия) или по 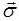(статические условия).

При этом должны выполняться условия совместимости деформаций:

связь между компонентами тензора деформаций и перемещениями.

2) Уравнение изгиба жестких пластин (плит) – уравнение Сафи Жермена, которое получается из уравнений равновесия (изгиба):

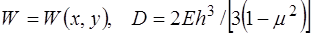- жесткость при изгибе, 2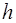- толщина пластины, для пластины на упругом основании, - реакция грунта, к- коэффициент.

3) Задача о кручении прямолинейных стержней сводится к решению уравнения

(3)

где 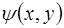функция напряжений, 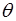- относительный угол закручивания.

Дифференциальные уравнения с частными

производными 2-го порядка

Дифференциальные уравнения с частными производными – уравнения вида

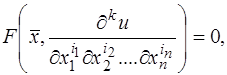(4)

F- заданная действительная функция точки 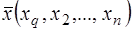области D евклидова пространства Еи действительных переменных

с неотрицательными целочисленными индексами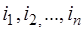

по крайней одна из производных

.

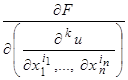Функция F отлична от нуля; m - натуральное число, называется порядком уравнения (4), неизвестная функция.

Если F линейная функция относительно производных то

уравнение (4) называется линейным.

При m=2 линейное уравнение имеет вид

(5)

где 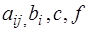- заданные функции в области D. Если для всех 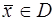, то (5) называется однородным.

Уравнение (5) в случае с постоянными коэффициентами при помощи линейного преобразования 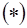можно привести к каноническому виду

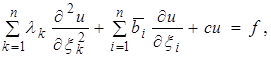(5.1)

где коэффициенты 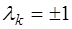или .

Рассмотрим классификацию уравнения 2-го порядка (5). Зафиксируем определенную точку 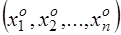в области D и составим квадратичную форму

. (6)

Уравнение (5) принадлежит к эллиптическому типу в точке 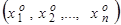, если в этой точке квадратичная форма (6) положительно определенная или отрицательно определенная.

Уравнение (5) принадлежит гиперболическому типу в точке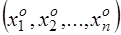, если в этой точке квадратичная форма (6) при приведении ее к сумме квадратов имеет все коэффициенты, кроме одного определенного знака, а оставшийся один коэффициент противоположного знака.

Уравнение (5) принадлежит параболическому типу в точке 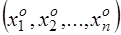, если в этой точке квадратичная форма (6) при приведении ее к сумме квадратов имеет только один коэффициент, равный нулю, а все другие коэффициенты имеют одинаковые знаки.

Наиболее часто встречаются уравнения в двумя независимыми переменными (частный случай уравнения (5)):

(7)

В этом случае с помощью преобразования 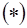уравнение (7) можно привести к каноническому виду

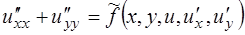, -эллиптическое уравнение (7.1)

- параболическое уравнение (7.2)

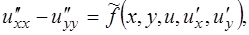-гиперболическое уравнение (7.3)

Для уравнения (7) принята следующая классификация:

1) 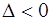- эллиптическое уравнение,

2) - уравнение параболического типа;

3) - уравнение гиперболического типа, где - дискриминант.

Если 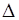меняет знак в области D, то уравнение смешанного типа.

Например, — уравнение Пуассона (Лапласа)- эллиптическое уравнение;

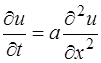- уравнение теплопроводности (диффузии) –

параболическое уранвение;

- волновое уравнение

(гиперболическое уравнение).

Постановка задачи Коши и краевых задач

Дифференциальные уравнения в частных производных имеют бесконечное множество решений, т.к. их общее решение зависит от произвольных функций. При решении конкретной физической задачи необходимо из множества решений выбрать то, которое удовлетворяет некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются граничные условия (условия на гранцице заданной области) и начальные условия, относящиеся к моменту времени, с которого начинается исследуемый процесс. Совокупность граничных и начальных условий называется краевыми условиями. Совокупность дифференциальных уравнений в частных производных и дополнительных условий представляет математическую формулировку физической задачи и называется задачей математической физики.

Нахождение решения дифференциального уравнения, удовлетворяющего начальным условиям (начальным данным), представляет собой задачу Коши.

Начальные данные задаются при 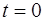, а решение отыскивается при . От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, заранее не указывается. Тем не менее и задачу Коши можно рассматривать как одну из краевых задач.

Задача нахождения решения дифференциального уравнения в некоторой области D, удовлетворяющего на границе D краевым условиям, является краевой задачей для дифф. уравнений с частными производными. Как правило, краевые условия связывают граничные значения решения с его производными до некоторого порядка (граничные условия 1-го,2-го,3-го,4-го рода).

Корректные и некорректные краевые задачи.

Методы решения дифференциальных уравнений.

Задача математической физики (краевая задача) является корректно поставленной, если ее решение удовлетворяет следующим условиям: 1) решение существует; 2) решение единственно; 3) решение устойчиво, т.е. малым изменениям исходных данных должны соответствовать малые изменения решения (непрерывно зависит от исходных данных).Если хотя бы одно из этих условий не выполняется, то задача некорректная. В этом случае решения могут существовать, могут и нет. На класс искомых решений и на заданные условия необходимо наложить дополнительные условия.

Если начальные данные заданы произвольно – характеристическая задача Коши, вообще говоря, не является корректно поставленной. Например, для уравнения теплопроводности 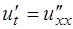характеристическая задача Коши 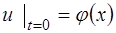корректна в классе функций, растущих на бесконечности не быстрее 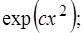если же показатель 2 при х заменить на , то единственности уже не будет. Существует широкий класс уравнений, для которых характеристическая задача может оказаться корректной (правильно поставленной).

Методы решения дифференциальных уравнений можно разделить на аналитические (они могут быть точные, приближенные (асимптотические, вариационные)) и численные (конечно-разностные методы).

Дата добавления: 2014-01-15