Частотная форма представления сигнала

При исследовании инвариантных во времени линейных систем решения всегда содержат комплексные экспоненциальные функции времени.

Широко используются представления детерминированных сигналов с применением базисных функций e^pt, как при P = ± jw (преобразование Фурье), так и при P = s + jw (обобщенное преобразование Фурье, известное как преобразование Лапласа).

Физически интерпретация преобразования Фурье:

использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром w) позволяет в соответствии с формулой Эйлера представить сложный детерминированный

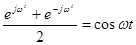(14)

сигнал в виде суммы гармонических составляющих. Поскольку параметр w в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.

Спектры периодических сигналов.

Периодические сигналы конечно не существуют, т.к. любой реальный сигнал имеет начало и конец. Однако при анализе сигналов в установившемся режиме можно считать, что они существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени. Они могут быть как в виде экспоненциальных составляющих, так и в виде гармоничных.

Пусть функция u(t) заданная на интервале [t₁, t₂] (t_{1 £} t _£ t₂) и удовлетворяющая условию Дирихле, повторяется с периодом 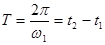на протяжении времени 0 -¥ до +¥.

Справка. Условие Дирихле: на любом конечном интервале функция должна быть непрерывной или иметь конечное число точек разрыва первого рода, а также конечное число экстремальных точек.

В точках разрыва t₀ функцию u(t) следует считать равной

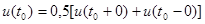
Если в качестве базисных выбраны экспоненциальные функции то выражение (5) запишется в виде:

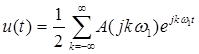(15)

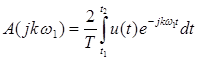(16)

Соотношение (15) представляет собой ряд Фурье в комплексной форме, содержащей экспоненциальные функции, как с положительным, так и с отрицательным параметром w (двустороннее частотное представление). Составляющие с отрицательными частотами являются следствием комплексной формы записи вещественной функции.

Функцию A(jkw₁) называют комплексным спектром периодического сигнала u(t). Этот спектр дискретный, т.к. функция A(jkw₁) определена на числовой оси только для целых значений k. Значение A(jkw₁) при конкретном k называют комплексной амплитудой.

Огибающая комплексного спектра A(jw) имеет вид:

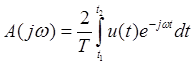(17)

Запишем комплексный спектр в форме:

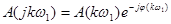(18)

Модуль комплексного спектра A(kw₁) называют спектром амплитуд, а функцию j(kw₁) – спектром фаз. Если известны A(kw₁) и j(kw₁), то в соответствии с (15) сигнал u(t) восстанавливается однозначно. Более важен параметр A(kw₁).

Поскольку A(kw₁) и j(kw₁) отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.

Воспользовавшись формулой Эйлера

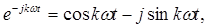
выразим комплексный спектр A (jkw ₁) в виде действительной и мнимой частей:

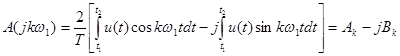(19)

где 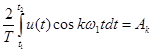(20)

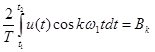(21)

Спектр амплитуд

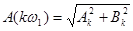(22)

является четной функцией k, т.е.

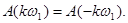(23)

Поскольку четность А_k и В_k противоположна, спектр фаз 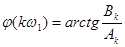- функция нечетная, т.е.

j(kw₁) = - j(-kw₁) (24)

При k =0 получаем постоянную составляющую

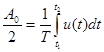(25)

От двустороннего спектрального представления легко перейти к одностороннему (не имеющему отрицательных частот), объединяя комплексно-сопряженные составляющие [см.(14)]. В этом случае получается ряд Фурье в тригонометрической форме.

Действительно, выделив в (15) постоянную составляющуюА₀/2 и суммируя составляющие симметричных частот w и -w, имеем

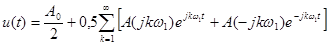(26)

учитывая (17) и (18) запишем

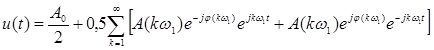
или

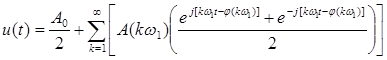
Воспользовавшись формулой Эйлера (14) и обозначив j(kw₁) через j_k, окончательно получим

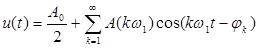(27)

Рассмотрена и другая тригонометрическая форма ряда Фурье, имеющая вид

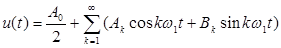(28)

Однако она менее удобна для практического применения.

Отдельные составляющие в представлениях (27) и (28) называют гармониками. Спектр амплитуд и фаз представляют спектральными диаграммами. Диаграмма спектра амплитуд представлена на рисунке 5.

Огибающую A(w) этого спектра амплитуду можно получить, заменив kw₁ в A(kw₁) на w₁, где w = kw₁ для k–й гармоники.

Поскольку спектры отображаются совокупностью линий, их часто называют линейчатыми. Аналогично представляются спектры фаз.

Распределение энергии в спектре.

Рассмотрим, как распределяется энергия сложного периодического сигнала u(t) по его спектральным составляющим. Под временной функцией u(t) будем подразумевать электрическое напряжение на резисторе в 1 Ом. Энергия W_T, выделяемая на этом резисторе за время, равное периоду колебаний Т.

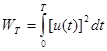(34)

Учитывая (15) получим

(35)

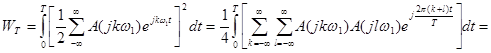
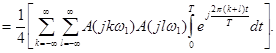
Определим значения интегралов в (35)

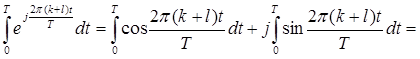
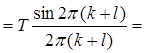(36)

Т.к. A(jkw₁) и A(- jkw₁) комплексно сопряжены, то

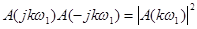(37)

С учетом (26), (36) и (37) выражение (35) имеет вид

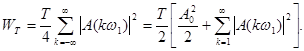(38)

Из (38) следует, что средняя за период энергия сложного периодического сигнала равна сумме средних значений, выделяемых на резисторе в 1 ОМ каждой его гармоникой в отдельности (включая постоянную составляющую).

С течением времени выделяемая энергия неограниченно растет, а средняя мощность остается постоянной

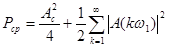(39)

Важно отметить, что она на зависит от фаз отдельных гармоник и, следовательно, будет сохранять свое значение при изменениях формы сигнала, обусловленных нарушениями фазовых соотношений гармоник спектра

Дата добавления: 2014-01-15