Геометрический метод вычисления вероятностей

Классический метод вычисления вероятностей

Из аксиоматического определения вероятности следует, что вероятность существует для любого события А Ì W, но как ее вычислить, об этом ничего не говорится, хотя известно, что для каждого элементарного события w_i существует вероятность р_i, такая, что сумма вероятностей всех элементарных событий пространства W равна единице, то есть

.

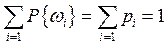На использовании этого факта основан классический метод вычисления вероятностей случайных событий, который в силу своей специфичности, дает способ нахождения вероятностей этих событий непосредственно из аксиом.

Пусть дано фиксированное вероятностное пространство (W,ℱ, Р), в котором:

а) W состоит из конечного числа n элементарных событий,

б) каждому элементарному событию w_i поставлена в соответствие вероятность

, .

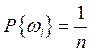Рассмотрим событие А Ì W, которое состоит из m элементарных событий: 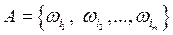, тогда из аксиомы 3 вероятностей, в силу несовместности элементарных событий, следует, что

.

Тем самым имеем формулу

, (2)

которую можно интерпретировать следующим образом: вероятность событию А произойти равна отношению числа элементарных событий, благоприятствующих появлению событию А, к числу всех элементарных событий из W.

В этом суть классического метода вычисления вероятностей событий.

Замечание. Приписав одинаковую вероятность каждому из элементарных событий пространства W, мы, с одной стороны, имея вероятностное пространство и опираясь на аксиомы теории вероятностей, получили правило вычисления вероятностей любых случайных событий из пространства W по формуле (2), с другой стороны, это дает нам основание считать все элементарные события равновозможными и вычисление вероятностей любых случайных событий из W свести к «урновой» схеме независимо от аксиом.

Из формулы (2) следует, что вероятность события А зависит только от числа элементарных событий, из которых оно состоит и не зависит от их конкретного содержания. Таким образом, чтобы воспользоваться формулой (2), необходимо найти число точек пространства W и число точек, из которых состоит событие А Ì W, но тогда это уже задача комбинаторного анализа.

Рассмотрим несколько примеров.

Пример 8. В урне из n шаров - k красных и (n - k) черных. Наудачу извлекаем без возвращения r шаров. Какова вероятность того, что в выборке из r шаров s шаров – красных?

Решение. Пусть событие { А } ~ {в выборке из r шаров s - красных}. Искомая вероятность находится по классической схеме, формула (2):

,

где - число возможных выборок объема r, которые различаются хотя бы одним номером шара, а m – число выборок объема r, в которых s шаров красных. Для , очевидно, число возможных вариантов выборки равно , а m, как следует из примера 7, равно 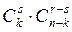. Таким образом, искомая вероятность равна

.

Пусть дан набор попарно несовместных событий A_s, 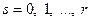, образующих полную группу, тогда

.

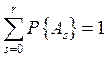В этом случае говорят, что имеем распределение вероятностей событий A_{s .}

Распределения вероятностей является одним из фундаментальных понятий современной теории вероятностей и составляет основу аксиомами Колмагорова.

Определение. Распределение вероятностей

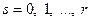, , (3)

определяется гипергеометрическое распределение.

Боровков А.А. в своей книге [2] на примере формулы (3) поясняет природу задач теории вероятностей и математической статистики следующим образом: зная состав генеральной совокупности, мы с помощью гипергеометрического распределения можем выяснить, каким может быть состав выборки – это типичная задача теории вероятностей (прямая задача). В естественных науках решают обратную задачу: по составу выборок, определяют природу генеральных совокупностей – это обратная задача, и она, образно говоря, составляет содержание математической статистики.

Обобщением биномиальных коэффициентов (сочетаний) являются полиномиальные коэффициенты, которые своим названием обязаны разложению полинома вида

,

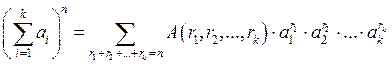где

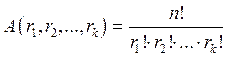, (4)

по степеням слагаемых.

Полиномиальные коэффициенты (4) часто применяются при решении комбинаторных задач.

Теорема. Пусть имеется k различных ящиков, по которым раскладываются пронумерованные шары. Тогда число размещений шаров по ящикам так, чтобы в ящике с номером r находилось r_i шаров, i = 1,2,… k, , определяется полиномиальными коэффициентами (4).

Доказательство. Поскольку порядок расположения ящиков важен, а шаров в ящиках - не важен, то для подсчета размещений шаров в любом ящике можно воспользоваться сочетаниями.

В первом ящике r₁ шаров из n можно выбрать способами, во втором ящике r₂ шаров, из оставшихся (n - r₁) можно выбрать 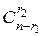способами и так далее, в (k – 1) ящик r_k-1 шаров выбираем 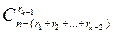способами; в ящик k – оставшиеся шаров попадают автоматически, одним способом.

Таким образом, всего размещений будет

._▼

Пример. По n ящикам случайно распределяются n шаров. Считая, что ящики и шары различимы, найти вероятности следующих событий:

а) {все ящики не пустые} = А₀;

б) {один ящик пуст} = А₁;

в) {два ящика пустых} = А₂;

г) {три ящика пустых } = А₃;

д) {(n -1) – ящик пуст} = А₄.

Решить задачу для случая n = 5.

Решение. Из условия следует, что распределение шаров по ящикам есть простой случайный выбор, следовательно, всех вариантов nⁿ.

Прежде, чем считать благоприятные варианты, опишем общий подход к их нахождению. Расположим (в порядке возрастания номеров) ящики, в которых находятся неразличимые шары, например,

333221…1.

Эта последовательность означает, что в первом, втором и третьем ящиках по три шара, в четвертом и пятом по два шара, в остальных (n – 5) ящиках по одному шару. Всего таких размещений шаров по ящикам будет . Так как шары на самом деле различимы, то на каждую такую комбинацию будем иметь 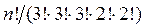размещений шаров. Таким образом, всего вариантов будет .

Переходим к решению по пунктам примера:

а) так как в каждом ящике находится по одному шару, то имеем последовательность 111…11, для которой число размещений равно n!/ n! = 1. Если шары различимы, то имеем n!/ 1! размещений, следовательно, всего вариантов m = 1× n!= n!, отсюда

.

б) если один ящик пуст, то какой-то ящик содержит два шара, тогда имеем последовательность 211…10, для которой число размещений равно n! × (n -2)!. Так как шары различимы, то для каждой такой комбинации имеем n!/ 2! размещений. Всего вариантов

,

тогда

.

в) если два ящика пусты, то имеем две последовательности: 311…100 и 221…100. Для первой число размещений равно n!/ (2! × (n – 3)!). На каждую такую комбинацию имеем n!/ 3! размещений шаров. Итак, для первой последовательности, число вариантов равно

.

Для второй последовательности всего вариантов будет

.

Окончательно имеем

.

Отсюда

.

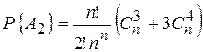г) для трех пустых ящиков будет три последовательности: 411…1000, либо 3211…1000, либо 22211…1000.

Для первой последовательности имеем

.

Для второй последовательности

.

Для третьей последовательности получаем

.

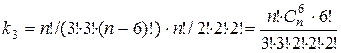Всего вариантов m = k₁ + k₂ + k₃,

или

.

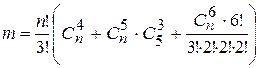Искомая вероятность равна

.

д) если (n -1) ящик пуст, то все шары должны находиться в одном из ящиков. Очевидно, что число комбинаций равно

.

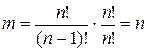Соответствующая этому событию вероятность равна

.

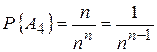При n = 5, имеем

,

,

,

,

.

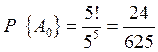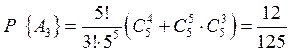Заметим, что при n = 5 события А_i должны образовывать полную группу, что соответствует действительности. В самом деле

Недостаток классического метода вычисления вероятностей в том, что он рассматривает конечное число равновозможных событий.

И если можно еще этот метод расширить на счетное число событий, то на большее его возможностей недостаточно. Однако идеи классического метода можно использовать на геометрических образах и, тем самым, рассматривать несчетные множества событий.

Пусть дана область Dⁿ из пространства Rⁿ, n = 1, 2, 3, с определенной на ней мере – mes Dⁿ (мера прямой – длина, мера плоскости – площадь, мера пространства – объем).

В области Dⁿ выделяется часть Аⁿ (вообще говоря, неодносвязная) с мерой mes Аⁿ.

В область Dⁿ наудачу бросается точка. Какова вероятность того, что эта точка попадет в область Аⁿ? Считая, как и при классическом подходе, попадание точки в область, пропорциональной только ее мере, будем иметь

,

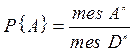где область Dⁿ соответствует пространству элементарных событий W, с той разницей, что Dⁿ не нормирована.

Пример 1. Вычислить вероятность того, что для наудачу взятого значения х Î[ 0, 2p), значение существует.

Решение. Обозначим через А искомое событие, а его геометрический образ через . Значение у существует, если 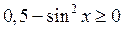, то есть 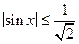, для х Î [ 0, 2p).

В силу симметрии, в качестве области D достаточно взять промежуток [0, p ], тогда mes D = p - 0 = p.

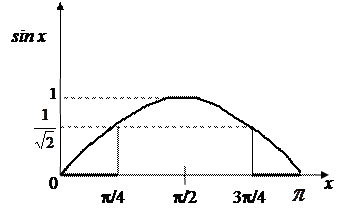
Рис. 1

Из рис. 1 видно, что область 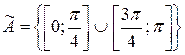, тогда . Окончательно, .

Пример 2 (Парадокс Бертрана). Наудачу берется хорда в круге. Чему равна вероятность того, что ее длина превосходит длину стороны вписанного равностороннего треугольника (событие А)?

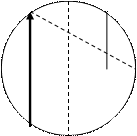
Решение 1. Из соображений симметрии, не нарушая общности, зададим направление хорды (рис. 2а).

х

а

	60^0

а) б)

Рис. 2

Проведем диаметр длиной d, перпендикулярный этому направлению. Очевидно, что эти и только эти хорды, пересекающие диаметр в промежутке 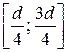, будут превосходить стороны правильного треугольника. В самом деле, сторона правильного треугольника а = 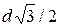, длина хорды находится из пропорции: . Таким образом .

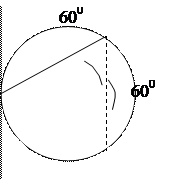
Решение 2. Из соображений симметрии, закрепим один конец хорды на окружности. Касательная к окружности в этой точке и две стороны правильного треугольника образуют углы по 60⁰ каждый. Задаче удовлетворяют только хорды, попадающие в средний угол, а это третья часть окружности. Отсюда .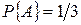

Решения задачи дают разные ответы, хотя логических противоречий нет. Суть в том, что в задаче не определено понятие проведения хорды наудачу. Так какой ответ верный?

Очевидно тот, который учитывает все возможные ситуации, то есть имеющий наибольшую вероятность. Ясно, что если будет построен геометрический аналог, с вероятностью превосходящей 0,5, то и ответ будет другой. Ответ .

Второе решение, с точки зрения теории вероятностей, дает результат для более частной задачи.

Дата добавления: 2014-01-15