Формула Пуассона

Приближенные формулы Муавра-Лапласа перестают быть эффективными при больших отклонениях вероятности р или q от 0,5 и бессмысленны при р ® 0, поскольку в этом случае, для разумного приближения, требуется проведение очень большого числа независимых испытаний.

Однако, во многих задачах пищевой промышленности, биологии, сельского хозяйства, в технике и электронике, возникают именно такие задачи, то есть приходится рассматривать объекты, состоящие из очень большого числа однородных элементов, каждый из которых имеет малую реализацию целевой функции (например, всхожесть зерна, выход из строя транзистора и др.).

Возникает задача оценки, например, вероятности всхожести семян, именно для таких случаев. Соответствующая оценка предложена Пуассоном.

Пусть в n независимых испытаниях вероятность появления события А, в каждом из испытаний, равна р (причем р близко к нулю), тогда имеет место оценка Пуассона:

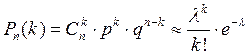, где l = np, k << n,

(где символ «<<» читается: «много меньше»).

В самом деле, при k = 0, имеем

.

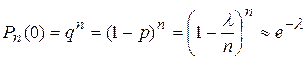Рассмотрим отношение

.

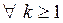
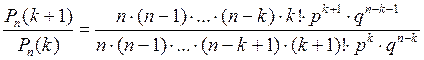После упрощений, получаем

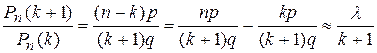, так как k << n, q ®1 и np = l.

Таким образом, имеем

, , .

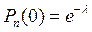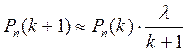Окончательно, получим

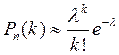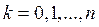, ._▼ (18)

Формула 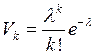, , 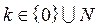называется формулой Пуассона. Очевидно, что .

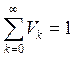Значения 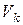формулы Пуассона для различных k и l представлены в приложении (табл. 2).

Пример. В книге на 1000 страниц 100 опечаток. Какова вероятность обнаружить, в наудачу взятой странице, хотя бы одну опечатку?

Решение. Имеем n = 100, р = 0,001, np = 0,1. В силу независимости выбора страниц искомая вероятность находится по формуле:

.

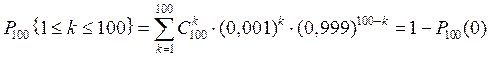Из формулы (18) получаем .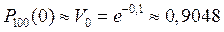

Таким образом, .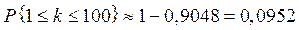

Полученное значение вероятности согласуется и с интуитивным смыслом, так как в среднем одна опечатка приходится на 10 страниц.

Рассмотренные нами приближенные формулы для формулы Бернулли имеют важное самостоятельное значение. В качестве приложения оценим событи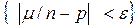е , где 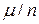- частота, e > 0.

Прежде всего, формулу (17), в интегральной теореме Муавра- Лапласа, преобразуем к виду:

.

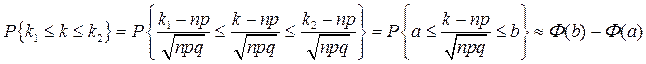Отсюда

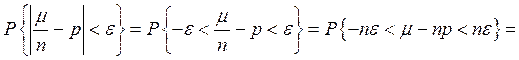
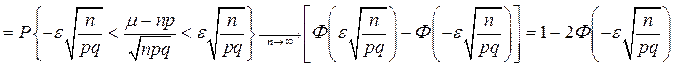. Таким образом:

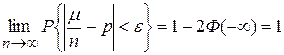. (19)

Асимптотическая формула (19) является одной из теорем закона больших чисел (теорема Бернулли п. 3.1); и обосновывает определение статистической вероятности (см. формулу 4, п.1.3.2.). Для практических приложений, вместо (19), обычно пользуются приближенной формулой:

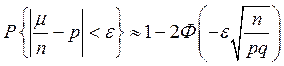. (20)

Это трансцендентное уравнение всегда имеет решение, если неизвестное только одно.

Пример. Сколько повторных испытаний симметричной монеты нужно провести, чтобы с вероятностью не меньшей 0,98, частота появления герба отклонилась от его вероятности не более чем на 0,01.

Решение. Из (20), при e = 0,01, р = 0,5, имеем

,.

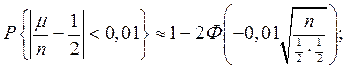
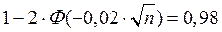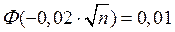По табл. 4 приложения значение аргумента находим из равенств

Ф (х) = 0,01Þ -0,02×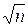= -2,3

или 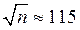Þ .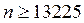

Дата добавления: 2014-01-15