Основы теории массового обслуживания

Под системой массового обслуживания (СМО) будем понимать комплекс, состоящий из а) случайного входящего потока требований (событий), нуждающихся в «обслуживании», б) дисциплины очереди, в) механизма, осуществляющего обслуживание.

Входящий поток. Для описания входящего потока обычно задается вероятностный закон, управляющий последовательностью моментов поступления требований на обслуживание и количеством требований в каждом поступлении (то есть требования поступают либо единичные, либо групповые). Источник, генерирующий требования, считается неисчерпаемым. Требование, поступившее на обслуживание, может обслуживаться сразу, если есть свободные обслуживающие приборы, либо ждать в очереди, либо отказаться от ожидания, то есть покинуть обслуживающую систему.

Дисциплина очереди. Это описательная характеристика. Требование, поступившее в систему, обслуживается в порядке очереди – дисциплина очереди: первым пришел – первым обслужен. Другая дисциплина очереди: последним пришел – первым обслужен - это обслуживание по приоритету. Наконец, обслуживание требований может быть случайным.

Механизм обслуживания. Характеризуется продолжительностью и характером процедур обслуживания. Обслуживание может осуществляться по принципу: на одно требование – один обслуживающий прибор. Если в системе несколько приборов, то параллельно могут обслуживаться несколько требований. Часто используют групповое обслуживание, то есть требование обслуживается одновременно несколькими приборами. В некоторых случаях требование обслуживается последовательно несколькими приборами – это многофазовое обслуживание.

По окончании обслуживания требование покидает систему.

Анализ системы массового обслуживания. Целью является рациональный выбор структуры обслуживания и процесса обслуживания. Для этого требуется разработать показатели эффективности систем массового обслуживания. Например, требуется знать: вероятность того, что занято или свободно k приборов; распределение вероятностей свободных или занятых приборов от обслуживания; вероятность того, что в очереди находится заданное число требований; вероятность того, что время ожидания в очереди привысит заданное. К показателям, характеризующим эффективное функционирование системы в среднем, относятся: средняя длина очереди; среднее время ожидания обслуживания; среднее число занятых приборов; среднее время простоя приборов; коэффициент загрузки системы и др. Часто вводятся экономические показатели. Разработкой математических моделей, получением числовых результатов и анализом показателей эффективности занимается теория массового обслуживания.

Таким образом, основные элементы системы массового обслуживания укладываются в следующую схему (рис. 30):

Рис. 30

Рассмотрим одну из задач теории массового обслуживания, ставшую уже классической.

Постановка задачи. Пусть имеем СМО, состоящую из n идентичных параллельных каналов (приборов) обслуживания, на которую поступает случайный поток требований интенсивностью a. Интервал времени между поступлениями соседних требований является случайной величиной x, образующей пуассоновский процесс

,

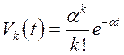где вероятность того, что за время t в СМО поступит ровно k требований, a - среднее число требований, поступающих в СМО в единицу времени.

Если требование поступившее в СМО застает все приборы занятыми, то оно встает в очередь и ждет до тех пор, пока не освободится обслуживающий прибор. Время обслуживания требования любым прибором является случайной величиной h, удовлетворяющий экспоненциальному закону распределения:

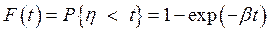
где , - среднее время обслуживания требования.

Каждый прибор, в любой момент времени t Î[0,¥), может обслуживать не более одного требования. Обслуженное требование покидает СМО. Требуется проанализировать эффективность работы системы.

Решение. Обозначим через 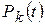- вероятность того, что в момент времени t в системе находится k требований.

Пусть D t – достаточно малый промежуток времени. Вероятность того, что в СМО за время D t не поступит ни одного требования:

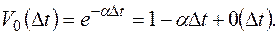
Вероятность того, что в СМО за время D t поступит одно требование:

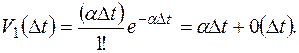
Вероятность того, что за время D t в СМО поступит два или более требований:

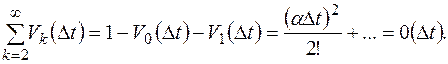
Вероятность того, что за время D t требование будет обслужено:

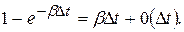
Вероятность того, что за время D t будет обслужено два или более требования:

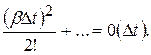
Вероятность того, что за время D t будет обслужено одно из к требований, находящихся в системе, найдем следующим образом:

=;

=;

=

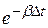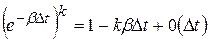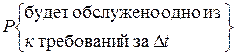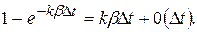
Вероятность того, что за время D t произойдет более одного события (например, поступит требование и какое – нибудь обслужится), есть бесконечно малая более высокого порядка, чем D t - 0 (D t).

Для 0 £ k £ n – 1 имеем разностное уравнение

. (95)

При получении уравнения мы воспользовались формулой полной вероятности и свойствами пуассоновского процесса.

В словесной формулировке это звучит так: вероятность того, что в момент времени (t+ D t) в системе находится к требований (k £ n – 1) равна вероятности того, что в момент t в системе находилось к требований и ни одного требования не поступило и не было обслужено, или вероятность того, что в момент времени t в системе находилось (k -1) требование и за время D t поступило одно требование в систему, или вероятность того, что в момент времени t в системе находилось (k +1) требование на обслуживании и за время D t одно из (k +1) требований было обслужено, или вероятность того, что за время D t произошло более одного события.

Преобразуем уравнение (95) к виду:

Разделив обе части на D t и переходя к пределу, получим

1£ к £ n -1. (96)

Для к ³ n заметим, что за время D t может быть обслужено не более чем одно из n требований, так как число обслуживающих приборов равно n.

Таким образом, для к ³ n, имеем уравнение

.

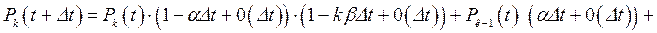
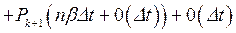Производя выкладки, аналогичные уравнению (95), получим

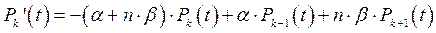. (97)

Заметим, что при к = 0, вероятность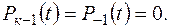

Учитывая это, окончательно имеем систему уравнений:

(98)

Пусть начальные условия имеют вид:

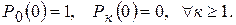(99)

Решение системы (98), с начальными условиями (99), слишком громоздко [8], однако решение для стационарного режима оказывается простым.

В самом деле, если (a/ nb) < 1, то СМО эргодична, то есть > 0 существует, но тогда .

Тем самым система (98) сводится к системе однородных алгебраических уравнений:

(100)

Чтобы система (100) имела единственное решение, добавим условие нормировки:

(101)

Для решения системы (100), с условием (101), введем обозначения

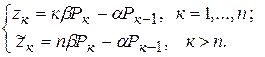(102)

В новых обозначениях, система (100) примет вид:

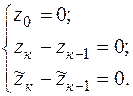
Отсюда следует, что

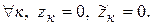
Возвращаясь к обозначениям (102), получаем

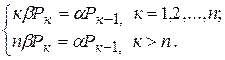
Выразим все вероятности через Р ₀. Имеем при к = 1

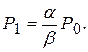
При 1< к £ n

. (103)

При к > n,

.

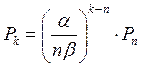или

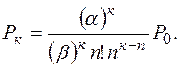(104)

Для нахождения Р ₀, воспользуемся условием нормировки (101):

.

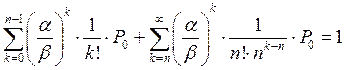После элементарных преобразований, получим

.

Учитывая, что имеем

(105)

Окончательно получаем:

,

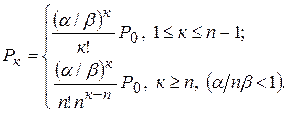
Замечание. Условие < 1, означает, что входящий поток меньше, чем суммарный выходящий, иначе ряд в (105) был бы расходящимся, то есть система не была бы эргодична.

Если Р _к известны, то многие показатели эффективности можно вычислить путем элементарных алгебраических операций, например,

1)

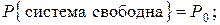
2)

3)

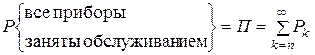
или

;

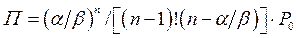4) ,

;

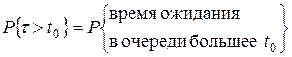5) t _ож – среднее время, в течение которого требование ждет начала обслуживания,

;

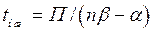6) А – средняя длина очереди,

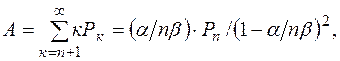
где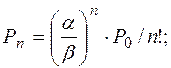

7) В - среднее число обслуживаемых требований,

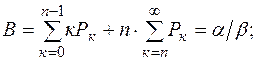
8) R - среднее число требований в системе,

R = A + B;

9) L – среднее время пребывания требования в системе,

/;

10)- коэффициент загрузки системы,

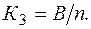
Будем считать, что предложенные здесь показатели эффективности (в зарубежной литературе их называют операционными характеристиками) дают достаточно полное представление о функционировании СМО.

Решение системы дифференциальных уравнений рождения и гибели вида (98), в переходном режиме, очень громоздко, да и, в ряде случаев, не является необходимым, поскольку реальные системы достаточно быстро входят в стационарный режим функционирования. Кроме того, учитывая, что получение необходимых формул для стационарного режима не вызывает особых трудностей, делает его привлекательным для анализа систем.

В ряде случаев получение алгебраических уравнений для стационарного режима можно записать сразу, если воспользоваться методом декомпозиции.

Суть метода. Функционирование системы S представляется в виде связного графа ее состояний Переход системы из состояния C_i в состояние С_j графически осуществляется по направленным отрезкам с заданными интенсивностями переходов . Если переход невозможен, то =0.

В стационарном режиме действует принцип равновесия: сумма «входов»

в любое состояние равна сумме «выходов» из него. Это позволяет записать уравнения равновесия по каждому из состояний (метод декомпозиции).

Рассмотрим применение метода декомпозиции на примере следующей задачи из теории надежности процесса гибели и рождения с конечным числом состояний [8].

Пусть имеем однородный марковский процесс с конечным числом состояний 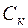, к = 0, 1, …, n. Если в момент t процесс находится в состоянии C_к, то за бесконечно малое время D t он с вероятностью перейдет в состояние , с вероятностью перейдет в состояние и с вероятностью останется в состоянии 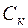. Если процесс находится, в момент t, в состоянии 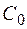, то за время D t он может остаться в состоянии 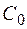или перейти в состояние ; если же процесс находится в момент t в состоянии , то за время D t он может остаться в состоянии или перейти в состояние 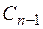. Обозначим через - вероятность того, что в момент времени t процесс находится в состоянии к, к = 0, 1, 2, …, n. Представим наш процесс в виде графической схемы (рис. 31).

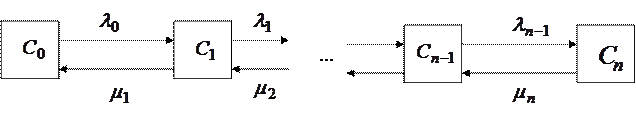
Рис. 31

Очевидно, что процесс эргодический, следовательно 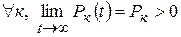. В силу условия равновесия, для стационарного режима, имеем (по каждому состоянию)

, ,

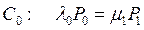для 1 £ к £ n -1, .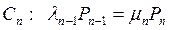

Таким образом, получаем однородную систему алгебраических уравнений:

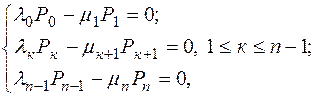(106)

которая имеет единственное решение, если добавить условие нормировки

(107)

Окончательно получаем:

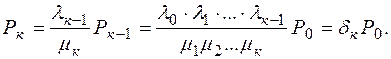
Учитывая (107) находим

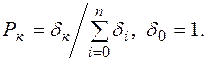
Упражнение. Записать граф – схему СМО предыдущей задачи, составить уравнения равновесия и получить значения вероятностей 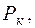к = 0,1,2,….

Замечание. Система уравнений вида (98) является частным случаем предельного перехода при 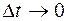в уравнениях Колмогорова – Чепмена для однородных во времени марковских процессах [2], которые имеют вид:

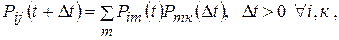(108)

где .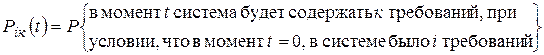

Система уравнений рождения и гибели отличается от системы (108) тем, что переходы возможны только из соседних состояний:

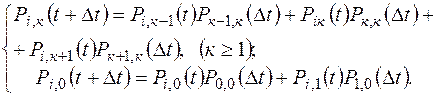(109)

Из системы (109), с точностью до обозначений, предельным переходом легко получить систему (98).

Дата добавления: 2014-01-15