Доверительный интервал

При применении критерия Колмогорова значения всех параметров теоретической функции распределения должны быть известны. При применении критерия c², для той же функции, параметры, если они неизвестны, оцениваются приближенно. (Например, для экспоненциального распределения параметр оценивается средним арифметическим). Естественно возникает вопрос: «В каких интервалах могут находиться оцениваемые параметры, чтобы гипотеза о соответствии эмпирической функции распределения теоретической была принята?»

Кроме того, если мы оцениваем только параметры, не зная функции распределения, нахождение допустимого интервала важно, например, для оценки ошибки принятого точечного значения параметра.

Мы приходим к задаче нахождения случайного интервала, покрывающего теоретический параметр. Прежде всего, на действительной прямой мы должны найти точку являющуюся серединой случайного интервала. В идеале это значение теоретического параметра, но мы его не знаем. Тогда берут такую точечную оценку , которая была бы наилучшим приближением к теоретическому параметру 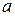(например, для оценки математического ожидания берут среднее арифметическое). Затем находят границы интервала . Значения e также случайны, следовательно, мы должны задать - вероятность того, что наш интервал покрывает теоретический параметр 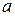. Итак, имеем уравнение

. (127)

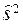Задача решалась бы просто, если бы мы знали закон распределения оценки , который на самом деле неизвестен. Однако, если оценивается математическое ожидание и дисперсия, а число опытов n > 20, то для них, в силу центральной предельной теоремы, считают закон распределения средней арифметической и дисперсии нормальным, тогда имеем из (127)

,

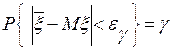а так как распределена нормально, то

(128)

где .

В уравнении (128) одно неизвестное - 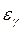, которое легко найти. Тогда доверительный интервал будет иметь вид.

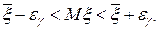(129)

Аналогичным образом можно получить доверительный интервал для дисперсии:

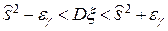. (130)

В целях удобства вычисления доверительных интервалов для математического ожидания и дисперсии вместо (129) и (130) рассматривают интервалы:

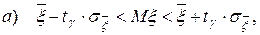(131)

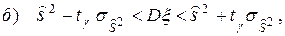(132)

где

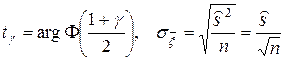(arg j – аргумент j),

Итак, если число испытаний n > 20, то для оценки математического ожидания и дисперсии доверительные интервалы, с удовлетворительной для практики точностью, находятся по формулам (129) и (130) или (131) и (132).

Более точные методы требуют, для построения доверительных интервалов, знать заранее вид закона распределения исследуемой случайной величины x.

Пример. Пусть имеем n = 22 результата измерения х₁, х₂,…, х₂₂ объема в мм³ некоторой физической величины: 3,1; 3,3; 2,9; 3,0; 3,1; 3,2; 2,8; 2,7; 3,1; 3,2; 2,9; 3,0; 2,9; 3,1; 2,8; 2,9; 3,2; 3,3; 2,9; 3,1; 3,2; 3,0. Построить доверительный интервал для математического ожидания Mx и дисперсии Dx.

Решение. Считая, что объем физической величины является случайной величиной x, распределенной по нормальному закону, воспользуемся формулами (131) и (132).

Имеем

.

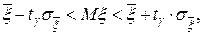
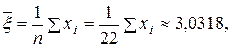
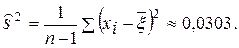
Отсюда, учитывая (131), 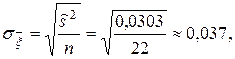а из (132), имеем

.

Значение Зададим g = 0,95, тогда

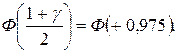
По табл. 3 приложения, находим .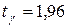

Таким образом, окончательно получаем

3,0318 – 1,96×0,037 < Mx < 3,0318+1,96×0,037,

0,0303 – 1,96×0,0094 < Dx < 0,0303+1,96×0,0094,

или 2,9593 < Mx < 3,1043,

0,0119 < Dx < 0,0487.

Предположение о нормальности закона распределения произвольной случайной величины далеко не всегда оправдано даже при больших выборках. В некоторых случаях удается построить доверительный интервал, относительно точно, если заменить закон распределения случайной величины x, содержащий неизвестные параметры, на достаточно близкий к ней закон распределения, этих параметров не содержащий. Мы рассмотрим здесь случай только нормально распределенной случайной величины с неизвестными параметрами а и s. Для этого потребуются следующие распределения:

1). Распределение Стьюдента (Госсетта). Плотность распределения Стьюдента (или t – распределения) c (n – 1) степенью свободы:

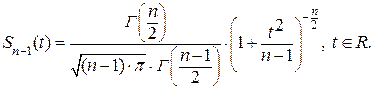(133)

Доказано, что, если x нормально распределенная случайная величина, то случайная величина подчинена закону (133).

2). Распределение c². Плотность распределения c² c (n -1) степенью свободы:

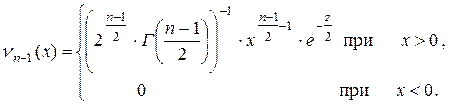(134)

Данное распределение имеет случайная величина где исправленная дисперсия нормально распределенной случайной величины x.

Легко заметить, что распределение Стьюдента (133) можно использовать при построении доверительного интервала для математического ожидания, а распределение c² (134) при построении доверительного интервала для дисперсии.

В самом деле, пусть доверительные интервалы для Мx и Dx определяются доверительной вероятностью b.

Построим доверительный интервал для Мx. Возьмем его симметричным относительно 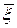, взяв за половину длины интервала. Ясно, что величина удовлетворяет равенству

.

Переходя от случайной величины 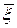к случайной величины h, распределенной по закону Стьюдента, получим

,

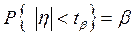где .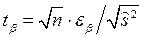

Значение 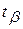найдем из условия (с учетом четности функции ):

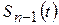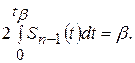(135)

При различных значениях доверительной вероятности b и числе испытаний n, значения 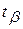представлены в табл. 7, приложения.

Таким образом, из условий:

и .

получаем доверительный интервал для оценки математического ожидания случайной величины x:

(136)

Для оценки дисперсии, рассмотрим распределение c² для случайной величины Зная закон распределения h, можно найти доверительный интервал, в который случайная величина h попадает с вероятностью .

Плотность имеет вид, изображенный на рис. 34.

Рис. 34

Выбрать интервал 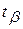так, как для оценки математического ожидания мы не можем, поскольку распределение c² не симметрично. Будем выбирать интервал 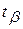таким образом, чтобы вероятность выхода случайной величины h за пределы интервала влево и вправо (заштрихованные области на рис. 31) были одинаковы и равны

Построение интервала с таким свойством сводится, очевидно, к выполнению условия

, (137)

где случайная величина h имеет распределение c² с r степенями свободы. При числе степеней свободы r = n -1, находим два значения c² из уравнения:

,

а) для левого конца интервала (рис. 34), при , имеем ;

б) для правого конца интервала, при , имеем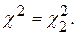

Соответствующие значения приведены в табл. 6, приложения.

Из (134) учитывая, что и (137), получаем:

а) для левого конца

б) для правого конца

Окончательно, доверительный интервал для оценки дисперсии имеет вид

(138)

Пример. Построить доверительный интервал для математического ожидания и дисперсии нормально распределенной случайной величины x

Решение. Дано: n = 22, число степеней свободы r = n -1 = 21, при доверительной вероятности b = 0,95:

а) для Mx имеем, из (136),

где 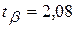получено из табл. 7, распределения Стьюдента, при r = 21 степени свободы и b = 0,95

Дата добавления: 2014-01-15