Установившийся режим в однородной линии.

Рассмотрим установившийся режим в однородной линии при синусоидальном источнике питания. Уравнения (1.2) для стационарного гармонического тока можно записать в комплексной форме:

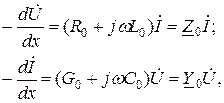(1.3)

где 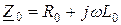- комплексное сопротивление единицы длины линии;

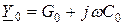- комплексная проводимость единицы длины линии.

Продифференцируем уравнения (1.3) по переменной х:

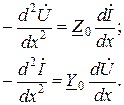
Вместо 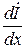и 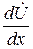в правой части подставим их значения из уравнений (1.3). Полу чим:

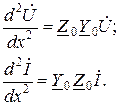(1.4)

Эти уравнения, определяющие изменения комплексных напряжений и токов вдоль линии, имеют одинаковый вид. Поэтому достаточно найти, например, закон изменения напряжения 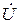, а ток получить из уравнений (1.3).

Решение линейного дифференциального уравнения второго порядка для комплексного напряжения 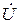имеет вид

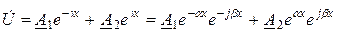, (1.5)

где 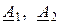- комплексные постоянные интегрирования;

γ - комплексная величина, называемая коэффициент распространения линии

(1.6)

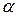- коэффициент затухания;

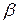- коэффициент фазы.

Ток согласно уравнению (1.3)

. (1.7)

Знаменатель, имеющий размерность сопротивления, называется волновым сопротивлением линии и обозначается 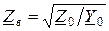. Рассматривая однородную линию как четырехполюсник, легко показать, что волновое сопротивление линии совпадает с характеристическим сопротивлением четырехполюсника. Поэтому в дальнейшем волновое сопротивление будем обозначать .

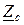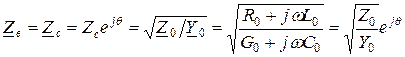, (1.8)

где 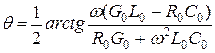- аргумент волнового сопротивления. (1.9)

Волновое сопротивление 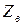и коэффициент распространения 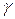называются вторичными параметрами однородной линии.

Подставив 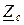в уравнение для тока (1.7), запишем

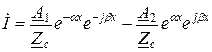. (1.10)

Так как 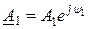и , то мгновенные значений напряжения и тока:

; (1.11)

. (1.12)

Каждое из слагаемых правой части двух последних уравнений можно рассматривать как бегущую волну, движущуюся в направлении возрастания или убывания координаты х и затухающую в направлении движения.

Основными характеристиками бегущей волны являются фазовая скорость и длина волны.

Фазовой скоростью волны с называется скорость перемещения фазы колебания, которая в течении времени t и по мере увеличения расстояния х, пройденного волной, остается постоянной, т.е.

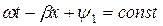, откуда 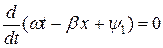, 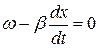и

, (1.13)

а для правого слагаемого уравнения (1.11) значение фазовой скорости такое же, но с обратным знаком. Следовательно, эти слагаемые могут рассматриваться как волны, движущиеся в противоположных направлениях.

Длиной волны 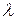называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых различаются на 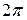. Следовательно, для первого слагаемого получим

,

откуда и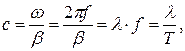

т.е. за время, равное периоду волна пробегает расстояние, равное длине волны.

Условимся волну, движущуюся от начала линии называть прямой, а движущуюся от конца линии – обратной.

Затухающая прямая волна представлена на рис. 1.2.

Выберем положительные направления напряжений и токов отдельных волн от прямого провода к обратному.

Из (1.11) и (1.12) следует, что напряжение 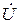есть сумма напряжений прямой и обратной волн, а ток 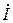- разность токов прямой и обратной волн, тогда

где .

Токи и напряжения как прямой, так и обратной волны связаны между собой законом Ома:

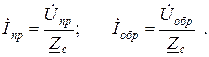(1.14)

Следует иметь в виду, что физически существуют только результирующие ток 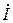и напряжение 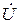, а разложение их на прямые и обратные волны лишь удобный прием.

Кривые распределения мгновенных значений напряжений и токов также имеют волнообразный характер (рис. 1.3).

Получим выражения для напряжения и тока в любой точке линии через напряжение и ток в начале линии.

Перепишем уравнения (1.5) и (1.7):

;

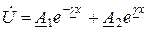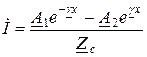, (1.15)

Предполагая, что в начале линии (х = 0) напряжение и ток 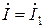, из уравнений (1.15) найдем постоянные интегрирования и .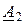

; ;

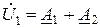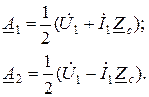(1.16)

С учетом (1.16) уравнения (1.5) и (1.7) для токов и напряжений в любой точке линии () можно записать так:

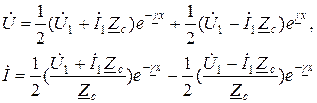. (1.17)

Подобным образом получим выражения для напряжения и тока в любой точке линии через напряжение и ток в конце линии:

. (1.18)

Дата добавления: 2014-01-15