Теорема Гаусса для однородной среды

Теорема Остроградского.

Теорема Остроградского (теорема дивергенции) - интеграл от дивергенции вектора, взятый па объему, можно заменить (потоком вектора через замкнутую поверхность, ограничивающую этот объем.

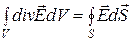. (2.19)

Однородная изотропная среда характеризуется диэлектрической проницаемостью , которая не зависит от координат (то есть можно вынести за знак дивергенции).

Теорема Гаусса– частный случай применения теоремы Остроградского для электрического поля. Она позволяет сравнительно быстро рассчитать поле (определить в каждой его точке), обладающее цилиндрической, сферической или плоской симметрией.

Теорема Гаусса в интегральной форме для однородной среды - поток вектора сквозь замкнутую поверхность не зависит от размера и формы поверхности, прямо пропорционален заряду, находящемуся внутри поверхности, и обратно пропорционален диэлектрической проницаемости среды

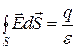. (2.20)

Доказательство. Пусть поле возбуждается зарядом q (см. рис. 2.9). Окружим этот заряд сферической поверхностью S ₀ с центром на заряде и любой другой поверхностью S. Обе поверхности пронизывает одно и то же число силовых линий, поэтому потоки вектора через поверхности будут равны

.

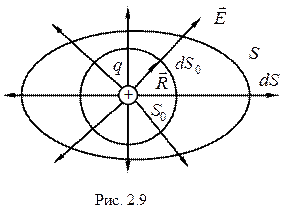
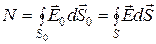Оба этих потока вычисляются в направлении внешних нормалей к соответствующим поверхностям.

В любой точке поверхности S ₀ вектор , по модулю 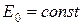и равно .

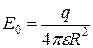Радиус вектор 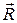совпадает по направлению с нормалью.

Поэтому

,

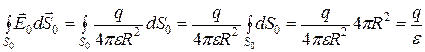т.е.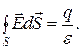

Если внутри объема, ограниченного поверхностью S, находится объемный заряд, то 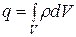и

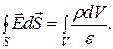
Заменим левую часть равенства по теореме Остроградского – Гаусса.

.

Последнее равенство справедливо, если подынтегральные функции равны, поэтому

. (2.21)

Это теорема Гаусса в дифференциальной форме для однородной среды.

Если заряд в данной точке поля отсутствует, то 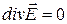. Уравнение показывает, что источником поля вектора является свободный заряд.

Если , т.е. поток вектора положителен, то данная точка поля является истоком векторного поля, если 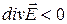, то – стоком.

Дата добавления: 2014-01-15