Пример. Уравнение сферы

Сферой в пространстве называется множество точек равноудаленных от заданной точки М₀(х₀;у₀;z₀) – центра сферы.

Пусть М(х;у;z) – некоторая переменная точка сфера. Расстояние от точки М до центра М₀ постоянно и равно радиусу сферы, т.е. d(M₀M)=const=R

R=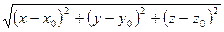

R²=(x-x₀)²+(y-y₀)²+(z-z₀)² – уравнение сферы.

Уравнения линия в пространстве R³.

Линия в пространстве определяется как пересечение двух поверхностей, т.е. как геометрическое место точек, находящихся одновременно на двух поверхностях.

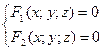(9) – общее уравнение линии в пространстве.

Линию как пересечение двух поверхностей в пространстве можно представить бесчисленным числом способов. Т.е. вместо системы (9) можно взять любую эквивалентную систему.

Параметрические уравнения линии и поверхности в пространстве.

Ли нию в пространстве можно так же задать параметрически:

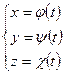(10)

где функции j(t), y(t) и c(t) определены и непрерывны в некотором промежутке изменения параметра t.

Покажем, что этот способ определения линии в пространстве эквивалентен определению линии как пересечения двух поверхностей.

Допустим, что хотя бы одна из трех функций, например c(t), имеет обратную. Тогда t=c^-1(z) подставляя это значение вместо t в первые два равенства (10), получим уравнения двух поверхностей x=j(c^-1(z)), y=y(c^-1(z)),

пересечением которых является данная линия.

Пример (с.115).

Классификация поверхностей.

Определение 1. Поверхность называется алгебраической, если в некоторой декартовой прямоугольной системе координат, если она определяется алгебраическим уравнением F(x;y;z)=0 с тремя переменными.

Определение 2. Всякая не алгебраическая поверхность называется трансцендентной.

Определение 3. Алгебраическая поверхность называется поверхностью порядка n, если в некоторой декартовой прямоугольной системе координат она определяется алгебраическим уравнением степени n с тремя переменными.

Установлению корректности определений 1,2,3 способствует следующая теорема.

Теорема (док-во на с.117). Если поверхность в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта поверхность и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени n.

Дата добавления: 2014-01-15