Принцип аргумента и критерий устойчивости Михайлова

Критерий Михайлова основан на так называемом принципе аргумента.

Рассмотрим характеристический полином замкнутой системы, который по теореме Безу можно представить в виде

D(p) = a ₀ pⁿ+ a ₁ p^{n- 1} +…+ a_n = a ₀ (p - p ₁ )…(p - p_n).

Сделаем подстановку p = jw

D(jw) = a ₀ (jw)ⁿ+ a₁(jw)^{n- 1} +…+ a_n = a ₀ (jw - p ₁ )…(jw - p_n) = X(w)+jY(w).

Для конкретного значения w имеет точку на комплексной плоскости, задаваемую параметрическими уравнениями

Если изменять w в диапазоне от -¥ до ¥, то будет прочерчена кривая Михайлова, т. е. годограф. Изучим поворот вектора D(jw) при изменении w от -¥ до ¥, т. е. найдем приращение аргумента вектора (аргумент равен сумме для произведения векторов): .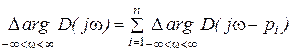

При w = - ¥ разностный вектор, начало которого в точке р _i, а конец на мнимой оси, направлен вертикально вниз. По мере роста w конец вектора скользит вдоль мнимой оси, а при w = ¥ вектор направлен вертикально вверх. Если корень левый (рис. 2.9.19а), то D arg = +p, а если корень правый, то D arg = -p.

Если характеристическое уравнение имеет m правых корней (соответственно n - m левых), то .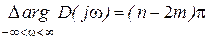

Это и есть принцип аргумента. При выделении действительной части Х(w) и мнимой Y(w) мы отнесли к Х(w) все слагаемые, содержащие jw в четной степени, а к Y(w) – в нечетной степени. Поэтому кривая Михайлова симметрична относительно действительной оси (Х(w) – четная, Y(w) – нечетная функция). В результате, если изменять w от 0 до +¥, то приращение аргумента будет в два раза меньше. В связи с этим окончательно принцип аргумента формулируется следующим образом . (2.9.29)

Если система устойчива, т.е. m = 0, то получаем критерий устойчивости Михайлова.

По Михайлову для устойчивости необходимо и достаточно, чтобы

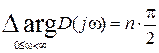, (2.9.30)

то есть кривая Михайлова должна последовательно проходить через n четвертей против часовой стрелки.

Очевидно, что для применения критерия Михайлова не требуется точного и детального построения кривой. Важно установить, каким образом она огибает начало координат и не нарушается ли последовательность прохождения n четвертей против часовой стрелки.

Необходимость условия устойчивости по критерию Михайлова. Необходимость заключается в том, что, если система устойчивая, то приращение аргумента вектора будет равным согласно формуле (2.9.30), что говорит о том, что система будет устойчивой.

Достаточность условия устойчивости по критерию Михайлова. Достаточность заключается в том, что приращение аргумента вектора гарантирует устойчивость, что не сложно проверить на примере.

Пример 2.9.6. Применить критерий Михайлова для проверки устойчи­вости системы, показанной на рис.2.9.20.

Характеристический полином замкнутой системы при k ₁ k ₂> 0 соответствует устойчивой системе, так условие Сто­долы выполняется, а для n = 1 оно достаточно. Можно непосред­ственно найти корень р ₁ = - k ₁ k ₂ и убедиться, что необходимое и достаточное условие устойчивости выполнено. Поэтому применение критерия Михайлова носит иллюстративный характер. Полагая p=jw, получим

D(jw) = X(w)+jY(w),

где Х(w) = 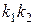; Y(w) = w. (2.9.31)

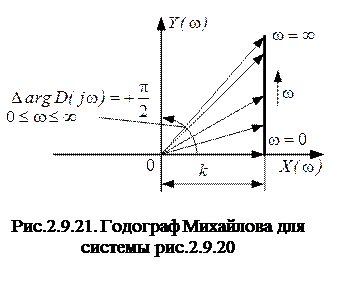
По параметрическим уравнениям (2.9.31) построен годограф Ми­хайлова на рис.2.9.21, из которого видно, что при изменении w от 0 до ¥ вектор D(jw) поворачивается против часовой стрел­ки на + p /2, т.е. система устойчива.

Дата добавления: 2014-01-15