
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимптоты графика функции
Вопрос
Вопрос
Вопрос
Вопрос
Вопрос
Правило Лопиталя (теорема Вернули – Лопиталя).
Пусть 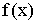 и
и 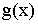 гладкие в окрестности
гладкие в окрестности  и
и 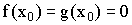
Тогда 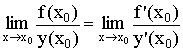
Правило Лопиталя: Предел отношения функций равен пределу отношения их производных.
Доказательство:
Применим теорему для 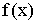 и
и 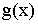 ,
, 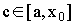 , где а - точка в окрестности
, где а - точка в окрестности  .
.
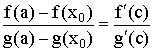 где
где 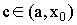 .
.
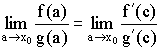

Примеры:
1) 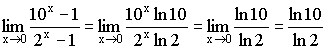
2) 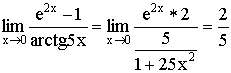
3) 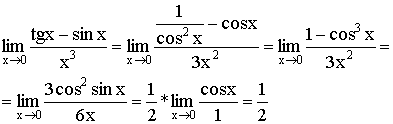
Неопределенности типа 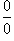
Пусть заданы две функции f (x) и g (x), такие, что
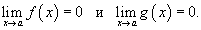
В этом случае говорят, что функция 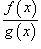 имеет неопределенность типа
имеет неопределенность типа 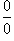 в точке x = a. Чтобы найти предел при x = a когда функция
в точке x = a. Чтобы найти предел при x = a когда функция 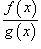 содержит неопределенность
содержит неопределенность 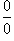 , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.
, нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.
Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.
Неопределенности типа 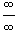
Пусть две функции f (x) и g (x) обладают свойством
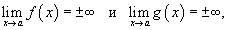
где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция 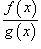 имеет в точке a неопределенность типа
имеет в точке a неопределенность типа 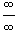 . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
. Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
Неопределенности типа 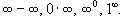
Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа 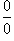 и
и 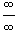 .
.
Формула Тейлора — Пеано Пусть 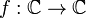 ,
, 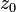 — предельная точка множества
— предельная точка множества  и
и 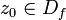 . Если функция
. Если функция 
 -дифференцируема в смысле Ферма — Лагранжа в точке
-дифференцируема в смысле Ферма — Лагранжа в точке 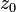 , то справедлива формула Тейлора — Пеано
, то справедлива формула Тейлора — Пеано
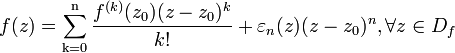
где εn(z) - непрерывная в точке z0 функция и εn(z0)=0. Применим метод математической индукции. Если n=0, то утверждение очевидно при εn (z)=f(z)-f(z0). Предположим, что утверждение теоремы справедливо после замены n на n-1 и что функция f n-дифференцируема в смысле Ферма-Лагранжа в точке z0. Согласно определению, существует такая n-1 дифференцируемая в смысле Ферма-Лагранжа в точке z0 функция φ, что ∀z∈Df,
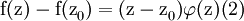
По предположению
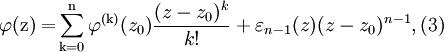
где 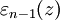 - непрерывная в точке z0 функция и
- непрерывная в точке z0 функция и 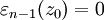 . Из равенств (2) и (3) получаем:
. Из равенств (2) и (3) получаем:
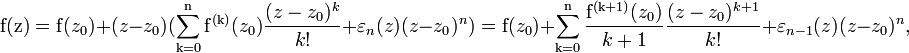
Что равносильно формуле (1) при 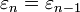
Основные разложения в ряд Тейлора
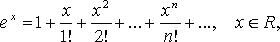
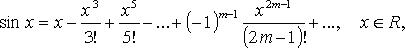
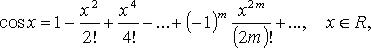
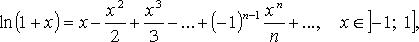
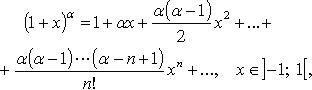
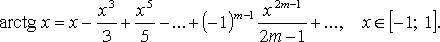
Необходимые и достаточные условия экстремума функции нескольких
(двух) переменных
Рассмотрим функцию 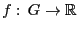 , где
, где 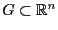 -- открытое множество.
-- открытое множество.
Определение 1. 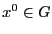 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если
, если
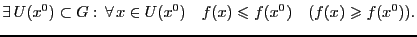
Аналогично если выполняется строгое неравенство, точка называется точкой строгого максимума (строгого минимума).
Теорема 1. (необходимое условие экстремума) Если 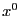 -- точка экстремума и существует
-- точка экстремума и существует 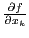 , то
, то  .
.
Доказательство. Частную производную можно представить как производную функции одной переменной 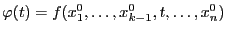 в точке
в точке 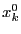 . Для этой функции точка
. Для этой функции точка 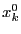 также является точкой экстремума. Тогда, по необходимому условию экстремума функции одной переменной
также является точкой экстремума. Тогда, по необходимому условию экстремума функции одной переменной 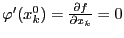 .
. 
Определение 2. 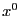 -- стационарная точка функции
-- стационарная точка функции  , если
, если  -- дифференцируема в этой точке и
-- дифференцируема в этой точке и 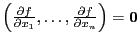 , или
, или  -- не дифференцируема в этой точке.
-- не дифференцируема в этой точке.
Замечание 1. Квадратичная форма -- многочлен вида 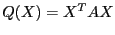 ,
,  -- положительно определена, если на положительных переменных она принимает положительные значения. Для квадратичных форм существует критерий Сильвестра: форма положительно определена, если все главные миноры ее матрицы положительны. Форма отрицательно определена, если
-- положительно определена, если на положительных переменных она принимает положительные значения. Для квадратичных форм существует критерий Сильвестра: форма положительно определена, если все главные миноры ее матрицы положительны. Форма отрицательно определена, если  положительно определена. Тогда главные миноры меняют знак, начиная с минуса.
положительно определена. Тогда главные миноры меняют знак, начиная с минуса.
Теорема 2. (достаточное условие экстремума) Если  дважды дифференцируема в стационарной точке
дважды дифференцируема в стационарной точке 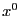 , то
, то 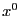 -- точка минимума (максимума), если квадратичная форма
-- точка минимума (максимума), если квадратичная форма 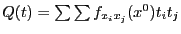 положительно (отрицательно) определена. Если эта форма не определена, то экстремума в этой точке нет. Если она вырождена, то неизвестно, является ли
положительно (отрицательно) определена. Если эта форма не определена, то экстремума в этой точке нет. Если она вырождена, то неизвестно, является ли 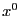 точкой экстремума.
точкой экстремума.
Доказательство. По формуле Тейлора приращение функции в точке 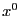 можно записать в виде
можно записать в виде 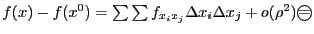 , поскольку, по необходимому условию экстремума, частные производные будут равны нулю. Перепишем выражение в виде
, поскольку, по необходимому условию экстремума, частные производные будут равны нулю. Перепишем выражение в виде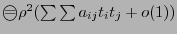 , причем
, причем  при
при 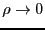 . Заметим, что новые переменные
. Заметим, что новые переменные 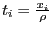 изменяются на единичной сфере, т.к.
изменяются на единичной сфере, т.к. 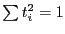 . Кроме того, квадратичная форма
. Кроме того, квадратичная форма 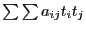 непрерывна и по теореме Вейерштрасса на сфере принимает наименьшее значение, обозначим его
непрерывна и по теореме Вейерштрасса на сфере принимает наименьшее значение, обозначим его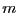 . Пусть форма положительно определена. Тогда
. Пусть форма положительно определена. Тогда 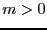 . Теперь благодаря тому, что
. Теперь благодаря тому, что  при
при 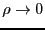 можно подобрать такое
можно подобрать такое  , что при
, что при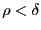 выполнено
выполнено  , тогда выполнено
, тогда выполнено 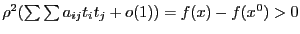 в этой окрестности. Что и означает, что
в этой окрестности. Что и означает, что 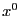 -- точка минимума. Для точки максимума доказательство аналогично.
-- точка минимума. Для точки максимума доказательство аналогично. 
Замечание 2. В случае двух переменных матрица квадратичной формы имеет вид  . Тогда если
. Тогда если 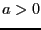 , то для положительной определенности достаточно
, то для положительной определенности достаточно 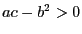 -- тогда имеется минимум. Если же
-- тогда имеется минимум. Если же 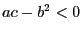 , то достигается максимум. Если же
, то достигается максимум. Если же 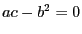 , то ничего сказать нельзя.
, то ничего сказать нельзя.
3.2.3. Выпуклость функции и точки перегиба
Непрерывная на отрезке [ a; b ] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x 1 и x 2 из этого отрезка

 График 3.2.3.1. Другими словами, если для любых точек x 1 и x 2 отрезка [ a; b ] секущая ABпроходит под графиком функции f (x), то функция f выпукла вверх.
График 3.2.3.1. Другими словами, если для любых точек x 1 и x 2 отрезка [ a; b ] секущая ABпроходит под графиком функции f (x), то функция f выпукла вверх.
Аналогично определяется функция, выпуклая вниз.
Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вверх, если для любого 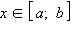

Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вниз, если для любого 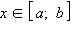
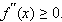
Так, вторая производная функции  равна
равна 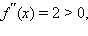 откуда следует, что квадратичная функция выпукла вниз на всей области определения.
откуда следует, что квадратичная функция выпукла вниз на всей области определения.
Пусть функция f (x) непрерывна в точке 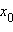 и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 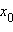 называется точкой перегибафункции f, если в этой точке изменяется направление ее выпуклости.
называется точкой перегибафункции f, если в этой точке изменяется направление ее выпуклости.
Необходимое условие наличия точки перегиба. Если 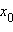 – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
– точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
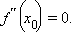
Достаточные условия наличия точки перегиба.
Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке 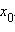 Если
Если 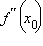 меняет знак при переходе через точку
меняет знак при переходе через точку 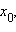 то
то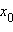 – точка перегиба функции f (x).
– точка перегиба функции f (x).
Если 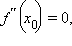
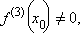 то
то 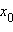 – точка перегиба функции f (x).
– точка перегиба функции f (x).
В заключение приведем примеры, когда точка x 0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
§ если функция разрывна в точке 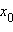 (например
(например 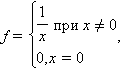
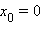 );
);
§ в случае угловой точки (например, 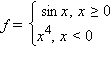
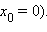
Не являются точками перегиба и точки возврата, например точка 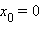 у функции
у функции 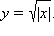
Все вышеперечисленные случаи изображены на рисунке.
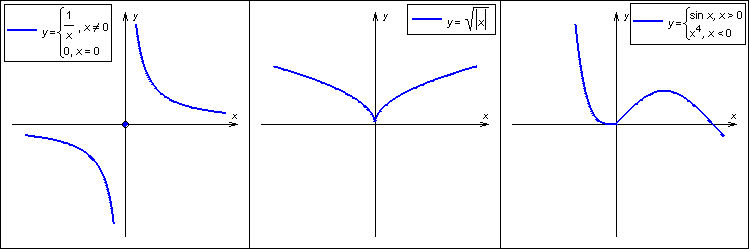 График 3.2.3.2.
График 3.2.3.2.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной асимптотой графика функции 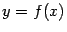 называется вертикальная прямая
называется вертикальная прямая 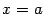 , если
, если 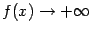 или
или 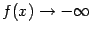 при каком-либо из условий:
при каком-либо из условий: 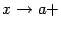 ,
, 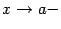 ,
, 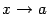 . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка 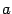 принадлежала области определения функции
принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 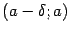 или
или 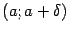 , где
, где 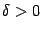 .
.
Пример 7.1 Рассмотрим функцию 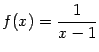 . График
. График 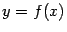 имеет вертикальную асимптоту
имеет вертикальную асимптоту 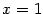 , поскольку при
, поскольку при 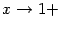 выполняется условие
выполняется условие  , а также при
, а также при 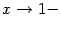 выполняется условие
выполняется условие 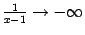 .
.
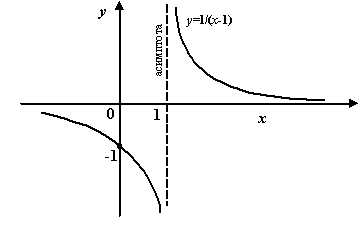
Рис.7.1.Вертикальная асимптота функции 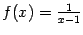
Пример 7.2 Рассмотрим функцию 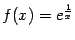 . Её график имеет вертикальную асимптоту
. Её график имеет вертикальную асимптоту 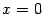 , так как
, так как  при
при  . То, что при
. То, что при 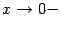 функция
функция  не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая
не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая 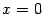 являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать,
являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать, 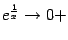 при
при 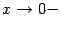 .)
.)
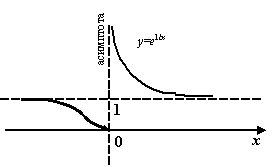
Рис.7.2.Вертикальная асимптота функции 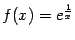
Пример 7.3 Рассмотрим функцию  . Прямая
. Прямая 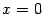 является вертикальной асимптотой графика
является вертикальной асимптотой графика 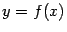 , так как
, так как 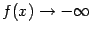 при
при  . Заметим, что слева от точки
. Заметим, что слева от точки 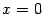 функция вообще не определена.
функция вообще не определена.
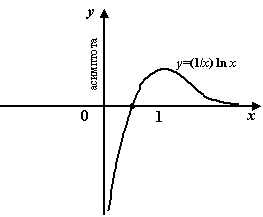
Рис.7.3.Вертикальная асимптота функции 
Пример 7.4 График функции  не имеет при
не имеет при 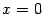 вертикальной асимптоты, так как
вертикальной асимптоты, так как  -- ограниченная (числом 1) и, следовательно, локально ограниченная при
-- ограниченная (числом 1) и, следовательно, локально ограниченная при 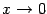 и не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция
и не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция  -- имеет вертикальную асимптоту
-- имеет вертикальную асимптоту 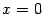 .
.

Рис.7.4.График функции  не имеет вертикальной асимптоты
не имеет вертикальной асимптоты
Пример 7.5 Прямая 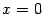 не является вертикальной асимптотой графика функции
не является вертикальной асимптотой графика функции 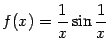 , поскольку здесь нельзя утверждать, что при
, поскольку здесь нельзя утверждать, что при 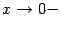 или
или  функция стремится к бесконечности. При некоторых малых значениях
функция стремится к бесконечности. При некоторых малых значениях 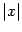 значения
значения 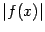 могут быть как угодно велики, однако при других малых
могут быть как угодно велики, однако при других малых 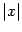 функция обращается в 0: так, при
функция обращается в 0: так, при 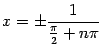 (
(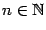 ) значения функции равны
) значения функции равны 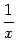 и стремятся к бесконечности при
и стремятся к бесконечности при 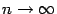 , а при всех
, а при всех 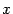 вида
вида  (
(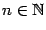 ) значения функции равны 0. В то же время как те, так и другие точки
) значения функции равны 0. В то же время как те, так и другие точки 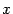 при увеличении
при увеличении 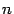 попадают всё ближе и ближе к точке 0. Значит, функция
попадают всё ближе и ближе к точке 0. Значит, функция  не является бесконечно большой при
не является бесконечно большой при 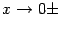 , и прямая
, и прямая 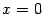 -- не асимптота.
-- не асимптота.
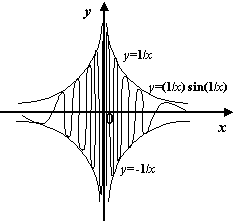
Рис.7.5.График функции 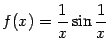 не имеет вертикальной асимптоты
не имеет вертикальной асимптоты
Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.
Определение 7.2 Наклонной асимптотой графика функции 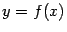 при
при  называется прямая
называется прямая 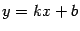 , если выполнены два условия:
, если выполнены два условия:
1) некоторый луч 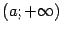 целиком содержится в
целиком содержится в 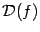 ;
;
2) расстояние по вертикали между графиком и прямой стремится к 0 при  :
:
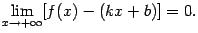
| (7.1) |
Наклонной асимптотой графика функции 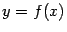 при
при 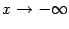 называется прямая
называется прямая 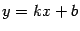 , если
, если
1) некоторый луч 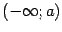 целиком содержится в
целиком содержится в 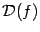 ;
;
2) расстояние по вертикали между графиком и прямой стремится к 0 при 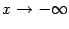 :
:
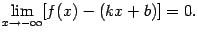

Рис.7.6.Графики функций, имеющие наклонные асимптоты при  и при
и при 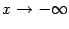
В случае, если наклонная асимптота расположена горизонтально, то есть при 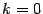 , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая
, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая 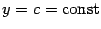 является горизонтальной асимптотой графика
является горизонтальной асимптотой графика 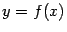 при
при  или
или 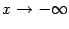 , если
, если
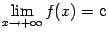
или
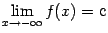
соответственно.
Пример 7.6 Рассмотрим функцию  . График этой функции имеет наклонную асимптоту
. График этой функции имеет наклонную асимптоту 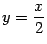 при
при  . Действительно,
. Действительно,
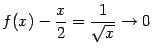 при
при 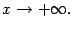
Однако эта функция не определена ни на каком луче вида 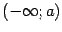 , так что её график не может иметь асимптоты при
, так что её график не может иметь асимптоты при 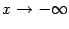 .
.
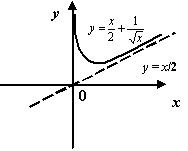
Рис.7.7.Наклонная асимптота функции 
Пример 7.7 График функции 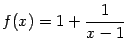 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 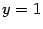 как при
как при  , так и при
, так и при 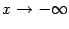 , поскольку, очевидно,
, поскольку, очевидно, 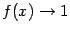 при
при 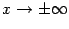 . Можно сказать также, что асимптота при
. Можно сказать также, что асимптота при 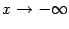 у этого графика совпадает с асимптотой при
у этого графика совпадает с асимптотой при  .
.

Рис.7.8.Горизонтальная асимптота функции 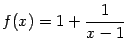
Аналогично определению наклонной асимптоты можно дать также более общее определение:
Определение 7.3 Линия 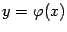 называется асимптотической линией графика функции
называется асимптотической линией графика функции  при
при  (или при
(или при 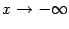 ), если обе эти функции определены на некотором луче
), если обе эти функции определены на некотором луче 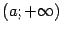 (или луче
(или луче 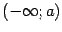 ) и разность ординат графиков стремится к 0 при
) и разность ординат графиков стремится к 0 при  (или при
(или при 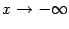 , соответственно).
, соответственно).
Если функция 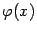 -- линейная, то есть график
-- линейная, то есть график 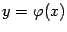 -- наклонная прямая, то асимптотическая линия -- это наклонная асимптота. Однако и другие линии бывает естественно рассматривать в качестве асимптотических.
-- наклонная прямая, то асимптотическая линия -- это наклонная асимптота. Однако и другие линии бывает естественно рассматривать в качестве асимптотических.
Пример 7.8 Рассмотрим функцию 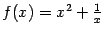 . При
. При 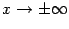 график этой функции имеет асимптотическую линию
график этой функции имеет асимптотическую линию 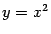 , поскольку разность между
, поскольку разность между  и
и 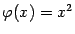 , равная, очевидно,
, равная, очевидно, 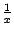 , стремится к 0 при
, стремится к 0 при 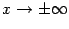 .
.
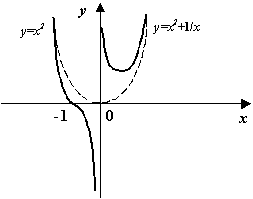
Рис.7.9.Асимптотическая линия 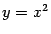 графика функции
графика функции 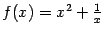
Замечание 7.1 Функции 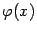 и
и  входят в определение асимптотической линии симметрично: если график
входят в определение асимптотической линии симметрично: если график 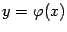 -- асимптотическая линия для графика
-- асимптотическая линия для графика 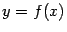 , то и
, то и 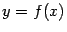 -- асимптотическая линия для
-- асимптотическая линия для 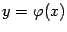 . На практике, однако, естественно считать асимптотической линией тот из двух графиков, который задаётся более простой формулой и вид которого известен.
. На практике, однако, естественно считать асимптотической линией тот из двух графиков, который задаётся более простой формулой и вид которого известен.
Пример 7.9 Рассмотрим функцию  . Так как
. Так как 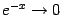 при
при  , то естественно рассматривать график
, то естественно рассматривать график 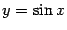 как асимптотическую линию при
как асимптотическую линию при  для графика исследуемой функции
для графика исследуемой функции  .
.
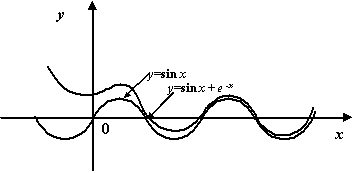
Рис.7.10.Асимптотическая линия 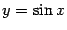 для графика функции
для графика функции  при
при 
Вернёмся к наклонным асимптотам -- прямым линиям с уравнением 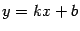 . Для их нахождения в тех случаях, когда значения
. Для их нахождения в тех случаях, когда значения 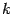 и
и 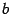 не очевидны, можно применять следующую теорему.
не очевидны, можно применять следующую теорему.
Теорема 7.1 Прямая 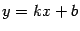 служит наклонной асимптотой для графика
служит наклонной асимптотой для графика 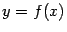 при
при  (или при
(или при 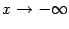 ) в том и только том случае, когда
) в том и только том случае, когда
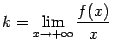
| (7.2) |
и
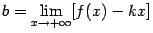
| (7.3) |
(соответственно, если
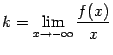 и
и 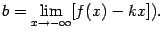
Таким образом, для нахождения наклонной (или горизонтальной, если получится 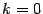 ) асимптоты достаточно найти два указанных предела
) асимптоты достаточно найти два указанных предела 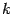 и, затем,
и, затем, 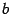 . Прямая
. Прямая 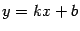 будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.
будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.
Доказательство теоремы. Докажем теорему в случае  ; доказательство при
; доказательство при 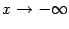 проводится совершенно аналогично.
проводится совершенно аналогично.
Перепишем условие (7.1), задающее асимптоту, в виде
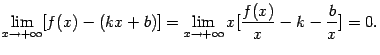
Так как первый множитель  , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть
, то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть
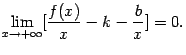
Но 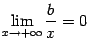 и
и 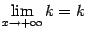 , так что
, так что
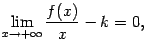
откуда следует равенство (7.2). Теперь число 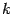 уже известно.
уже известно.
Подставляя это число в формулу (7.1), находим, что
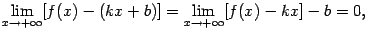
откуда следует равенство (7.3).
Пример 7.10 Найдём наклонные асимптоты графика 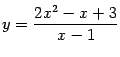 .
.
Попробуем отыскивать сразу оба предела, и при  , и при
, и при 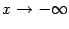 .
.
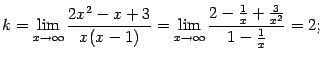
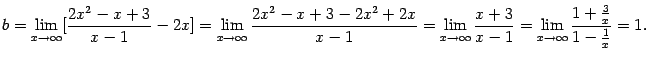
Итак, и при  , и при
, и при 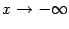 имеем
имеем 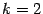 и
и 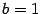 , так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение
, так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение 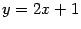 , то есть, фактически, асимптота только одна.
, то есть, фактически, асимптота только одна.
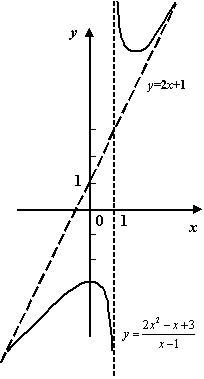
Рис.7.11.График 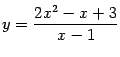 и его наклонная асимптота
и его наклонная асимптота
Замечание 7.2 Из определения асимптоты не следует, что если асимптоты при 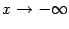 и при
и при  для одного и того же графика существуют, то они непременно совпадают. Это могут быть и различные прямые, как показывает следующий простой пример.
для одного и того же графика существуют, то они непременно совпадают. Это могут быть и различные прямые, как показывает следующий простой пример.
Пример 7.11 Рассмотрим график 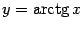 . При
. При 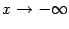 график приближается к горизонтальной асимптоте
график приближается к горизонтальной асимптоте 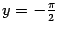 , а при
, а при  -- к другой горизонтальной асимптоте
-- к другой горизонтальной асимптоте 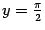 .
.
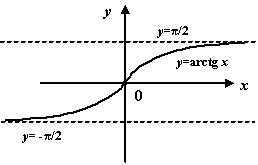
Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты
Различными могут оказаться и не обязательно горизонтальные асимптоты:
Пример 7.12 Рассмотрим функцию 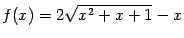 . Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.
. Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.
Сначала найдём асимптоту 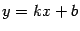 при
при  . Согласно доказанной теореме, имеем:
. Согласно доказанной теореме, имеем:
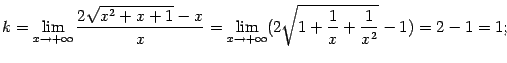
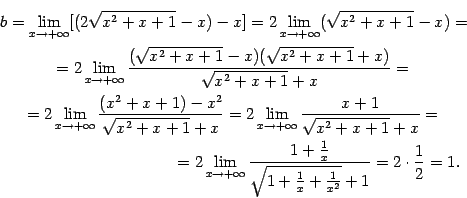
Таким образом, при  наклонной асимптотой служит прямая
наклонной асимптотой служит прямая 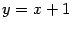 .
.
Теперь найдём асимптоту при 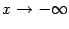 . Имеем:
. Имеем:
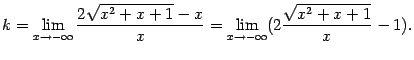
Поскольку 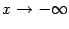 , мы можем считать, что в допредельном выражении
, мы можем считать, что в допредельном выражении  . В полученной дроби поделим числитель и знаменатель на положительное число
. В полученной дроби поделим числитель и знаменатель на положительное число 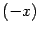 . Тогда под корнем нужно будет поделить на
. Тогда под корнем нужно будет поделить на  , и получится:
, и получится:
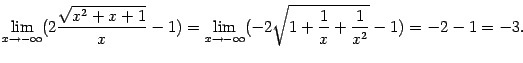
Вычисление 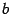 проведите сами в качестве упражнения. При этом получается
проведите сами в качестве упражнения. При этом получается 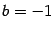 , так что наклонная асимптота при
, так что наклонная асимптота при 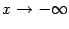 имеет уравнение
имеет уравнение 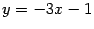 .
.

Рис.7.13.График 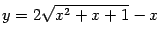 и его две наклонных асимптоты
и его две наклонных асимптоты
Замечание 7.3 Если график 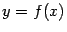 имеет асимптоту
имеет асимптоту 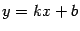 (например, при
(например, при  ) и существует предел производной:
) и существует предел производной:
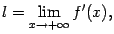
то 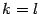 . Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты 17.
. Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты 17.
Однако асимптота может существовать и в случае, когда производная  не имеет никакого предела при
не имеет никакого предела при  . Дело в том, что значения
. Дело в том, что значения  могут совершать мелкие, но частые колебания относительно ординаты асимптоты, так что значения производной могут при этом испытывать незатухающие колебания. Проиллюстрируем эту возможность следующим примером.
могут совершать мелкие, но частые колебания относительно ординаты асимптоты, так что значения производной могут при этом испытывать незатухающие колебания. Проиллюстрируем эту возможность следующим примером.
Пример 7.13 Рассмотрим функцию 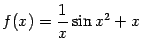 . Очевидно, что прямая
. Очевидно, что прямая 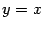 -- это асимптота графика
-- это асимптота графика 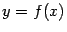 при
при  , так как первое слагаемое имеет предел, равный 0, при
, так как первое слагаемое имеет предел, равный 0, при  . Однако вычисление производной даёт
. Однако вычисление производной даёт
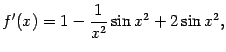
а эта функция при росте  совершает колебания, причём при больших
совершает колебания, причём при больших  второе слагаемое становится пренебрежимо малым, и значения
второе слагаемое становится пренебрежимо малым, и значения  колеблются примерно между
колеблются примерно между 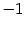 и 3. Следовательно, производная не имеет предела при
и 3. Следовательно, производная не имеет предела при  .
.
Если же рассмотреть функцию 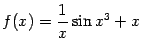 , то её производная оказывается даже неограниченной на любом луче вида
, то её производная оказывается даже неограниченной на любом луче вида 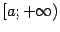 , хотя прямая
, хотя прямая 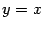 по-прежнему служит асимптотой графика
по-прежнему служит асимптотой графика 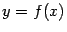 (проведите вычисления, доказывающие это, самостоятельно в качестве упражнения).
(проведите вычисления, доказывающие это, самостоятельно в качестве упражнения).
Не так уж редко встречается случай, когда, найдя наклонные и вертикальные асимптоты графика и исследовав поведение функции слева и справа от вертикальных асимптот, мы уже достаточно хорошо можем представить себе поведение функции.
Пример 7.14 Рассмотрим функцию 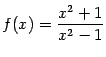 . Мы можем заметить, что
. Мы можем заметить, что  -- чётная функция, поскольку она зависит только от
-- чётная функция, поскольку она зависит только от 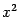 и, следовательно, не меняет знак при смене знака
и, следовательно, не меняет знак при смене знака 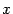 . Заметим также, что
. Заметим также, что 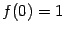 .
.
Знаменатель обращается в 0 при  , то есть
, то есть 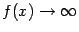 при
при 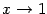 и при
и при 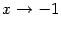 . Тем самым, прямые
. Тем самым, прямые 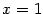 и
и 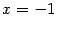 -- это вертикальные асимптоты. Подробнее разберём порведение функции при приближении
-- это вертикальные асимптоты. Подробнее разберём порведение функции при приближении 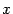 к
к 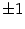 . Если
. Если 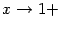 , то
, то 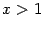 и, следовательно,
и, следовательно, 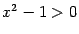 . Числитель
. Числитель 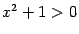 при всех
при всех 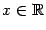 , так что дробь
, так что дробь  положительна. Значит,
положительна. Значит, 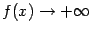 при
при 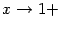 . При
. При 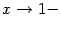 (и
(и 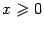 ) имеем
) имеем  , поэтому
, поэтому 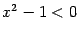 и
и  , так что
, так что 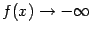 при
при 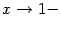 . Вследствие чётности функции получаем также, что
. Вследствие чётности функции получаем также, что 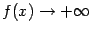 при
при 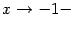 и
и 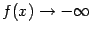 при
при  .
.
Найдём теперь наклонные асимптоты. Вычисляя параметры 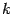 и
и 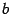 по формулам (7.2) и (7.3), получаем:
по формулам (7.2) и (7.3), получаем:
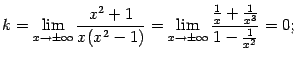
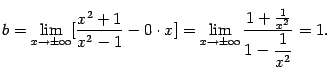
Таким образом, асимптоты при  и при
и при 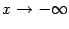 совпадают и имеют уравнение
совпадают и имеют уравнение 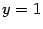 .
.
Суммируя сказанное, мы можем представить себе, что график функции ведёт себя примерно так:

Рис.7.14.График функции 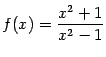
|
|
Дата добавления: 2014-01-15; Просмотров: 1135; Нарушение авторских прав?; Мы поможем в написании вашей работы!