Теорема Моода

При организации контроля качества следует учитывать теорему Моода. Пусть из партии объёма N берётся выборка объёма n. Количество несоответствующих изделий в партии D есть случайная величина, которая с разной вероятностью может, в принципе, принимать любое значение из диапазона от 0 (ни одного несоответствующего изделия в партии) до N (все изделия в партии несоответствующие). Для числа несоответствий в партии как для любой случайной величины существует закон распределения (производственный процесс как генератор случайных чисел, генерирует числа несоответствий в партии по определённому в вероятностном смысле закону), т.е. каждому значению D в партии можно сопоставить вероятность Р(D = i), где iÎ 0…N. Следовательно, существует математическое ожидание и дисперсия числа несоответствий в партии:

M[D] =;

D[D] =.

Теорема Моода утверждает:

Коэффициент корреляции r между числом несоответствий в выборке d и числом несоответствий в непроверенном остатке партии (D – d) есть величина

положительная: r > 0, если > 1 (т.е. если D[D] > M);

равная нулю: r = 0, если = 1 (т.е. если D[D] = M);

отрицательная: r < 0, если ≤ 1 (т.е. если D[D] < M),

где М = M[D] (1 - ).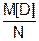

Таким образом, теорема Моода показывает, в каких случаях, при каком законе распределения выборочный контроль имеет смысл. Действительно, если корреляция как стохастическая связь между числом несоответствий в выборке и в непроверенном остатке партии отсутствует (r = 0) или отрицательная (r < 0), проводить выборочный контроль не имеет смысла, поскольку в этих случаях он не даёт никакой полезной информации. Выборочный контроль имеет смысл только в случае, когда r > 0, т.е. когда D[D] > M.

ПРИМЕР. Закон несоответствующих изделий в партии соответствует закону Бернулли (биноминальное распределение): Р = D/N = const. Тогда:

M[D] = N×P; D[D] = N×P(1 – Р) и М = N×P(1 – NP/N) = N×P(1 – Р).

Следовательно, = 1, т.е. проводить выборочный контроль в этом случае нет смысла. (Дело в том, что, если доля несоответствующих изделий в партии Р нам известна и она постоянна от партии к партии, то выборочный контроль никакой дополнительной информации относительно качества партии не даёт. Остаётся только констатировать, что в партиях число несоответствующих изделий D = N×P (где Р = const) и либо принимать эти партии, если это число меньше значения, установленного в договоре между поставщиком и потребителем, либо проводить сплошной контроль с отбраковкой несоответствующих изделий перед поставкой партии потребителю и дорабатывать технологический процесс производства с целью уменьшения значения Р до приемлемого уровня).

1. Уместен ли выборочный контроль в случае распределения Пуассона?

2. Уместен ли выборочный контроль в случае, когда про распределение несоответствующих изделий в партии ничего не известно?

Дата добавления: 2014-01-15