Выборочный контроль и проверка статистических гипотез

В курсе «Теория вероятностей и математическая статистика» рассматриваются процедуры проверки статистических гипотез с точки зрения общей теории принятия решений в условиях неопределённости. Очевидно, что контроль качества выборочными методами является частным случаем принятия решения в условиях недостатка информации о свойствах партии, поскольку в нашем распоряжении имеются данные только о части продукции – выборке, по которым необходимо сделать надёжное заключение о соответствии или несоответствии всей партии. В общем виде, при контроле качества продукции основная или нулевая гипотеза формулируется следующим образом:

Н₀: { продукция или партия изделий соответствует установленным в НТД требованиям } против альтернативной гипотезы Н₁: { продукция или партия изделий не соответствует требованиям }.

Стандартные методы контроля качества, о которых мы в основном и будем вести речь, разработаны для групповых показателей качества. Для альтернативных показателей это уровень несоответствий в партии, задаваемый в виде доли (или процента) несоответствующих единиц продукции или в виде числа несоответствий на 100 единиц продукции. Для количественных признаков все стандарты по приёмочному контролю качества разработаны для проверки требования в виде доли несоответствующих изделий в партии при условии нормального закона распределения признака качества. В качестве групповых показателей качества могут использоваться и такие характеристики партии как математическое ожидание и дисперсия (или стандартное отклонение). Причина, по которой в стандартах используется именно доля несоответствий в том, что этот показатель является информативно более ёмким, чем m или s². В самом деле, если необходимо проконтролировать партию изделий, количественный признак качества которой y должен находиться в пределах от а до b (изделие годное, если а £ y £ b), то при нормальном распределении признака y в соотношение для доли несоответствующих изделий q по (2.7) (см. так же рисунок 2.2) входят оба групповых показателя m и s², т.е. показатель q автоматически учитывает оба параметра распределения признака качества.

Таким образом, выражая нулевую гипотезу через численный параметр (групповой показатель), мы переходим от «вербальной» (словесной) формулировки гипотезы к параметрической, т.е. представляем смысловое ядро нулевой гипотезы через ограничение на параметры, которые можно тем или иным способом вычислить или оценить по выборке:

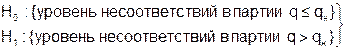для стандартных методов контроля

или для нестандартных методов, когда требования к качеству партии в НТД установлены, например, в виде: «партия соответствует требованиям и может быть поставлена потребителю, если m_нн £ m_п £ m_нв»]:

1) Н₀: {m_нн £ m_п £ m_нв} против Н₁: { m_п < m_нн OR m_п > m_нв};

2) Н₀: {s²_п £ s²_н} против Н₁: {s²_п > s²};

(где индекс «н» относится нормированному значению, а индекс «п» - к значению в партии).

1. Почему требования к среднему значению (мат. ожиданию) в партии может быть в виде как одностороннего, так и двустороннего ограничения, а требование к дисперсии или к стандартному отклонению целесообразно задавать только в виде одностороннего ограничения сверху?

2. Как связано требование к дисперсии с требованием к стандартному отклонению? Почему с точки зрения статистики правильнее задавать требование к дисперсии, а не к стандартному отклонению?

Примечание. В ГОСТе Р 50779.21 показано каким образом правильно строить и проверять гипотезы относительно математического ожидания и дисперсии (стандартного отклонения) генеральной совокупности.

После представления нулевой гипотезы в параметрическом виде нужно выбрать подходящую тестовую статистику, принимающую различные значения в зависимости от степени адекватности (соответствия) выборочных значений и предположения, сформулированного в нулевой (основной) гипотезе. Чтобы эта статистика могла служить критерием принятия или непринятия исходной гипотезы необходимо, чтобы она обладала определёнными свойствами. В общей теории проверки статистических гипотез эти свойства определены понятием «достаточная статистика». Достаточная статистика – это функция от выборочных значений, содержащая в наиболее сжатом виде всю информацию о распределении генеральной совокупности и её параметрах, и которая позволяет смысловую нагрузку числового параметра нулевой гипотезы представить в вероятностно-статистической форме. (В книге /1/ достаточная статистика сформулирована в виде скалярной функции g(x) (где х ={x₁, x₂, x₃, …, x_n} – вектор выборочных значений), которая названа «контрольной величиной», заменяющей выборку. В лекциях по «Теории вероятностей и математической статистике» достаточная статистика представлена в виде критерия К(x)).

Например, известно (строго доказано), что распределение выборочного среднего , рассчитываемого по выборке объёма n из нормально распределённой генеральной совокупности, также принадлежит к нормальному закону распределения, но с параметрами (m; s²/n), т.е. определяется параметрами m и s² распределения генеральной совокупности. Следовательно, вероятность того, что значение выборочного среднего примет то или иное конкретное значение полностью определяется параметрами той совокупности, из которой берётся выборка. Но верно и «обратное» утверждение: если получено конкретное значение выборочного среднего, то параметры генеральной совокупности, из которой была взята выборка, должны быть такими, чтобы вероятность полученного конкретного значения выборочного среднего была достаточно высока. Таким образом, выборочное среднее может служить критерием адекватности предположения, сформулированного в виде гипотезы Н₀ и фактическими значениями в выборке и, следовательно, вероятность полученного значения выборочного среднего можно принять за меру степени адекватности предположения о верности нулевой гипотезы. Очевидно, что вероятность получения любого значения выборочного среднего легко рассчитывается, если «встать» на позицию нулевой гипотезы, что и позволяет принять выборочное среднее в качестве тестовой статистики при проверке различных предположений о параметрах нормально распределённой генеральной совокупности. (Существует, так называемый «критерий факторизации» в виде теоремы Неймана-Фишера, который не только позволяет проверять обладает ли та или иная статистика свойством достаточности, но и «подсказывает» как её находить.)

В методах приёмочного контроля качества тестовые статистики построены на основе функционального оператора в виде суммы:

выборочное среднее =;

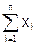выборочная дисперсия S =;

«отношения Стьюдента» t = 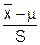, которое подчиняется распределению Стьюдента с n-1 степенью свободы;

«дисперсионного отношения» c²=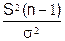, которое подчиняется распределению Пирсона c² с n-1 степенью свободы.

При проверке альтернативных признаков качества практически всегда используется сумма несоответствий в выборке, вероятность конкретного значения которой можно вычислить, используя, например, модель в виде гипергеометрического распределения, исходя из «верности» предположения о числе несоответствий или доли несоответствий q =D/N в контролируемой совокупности, т.е. в партии (см. раздел 2.3).

Поскольку тестовая статистика является скалярной функцией g(x) от векторного аргумента – выборочных значений, то все её возможные значения можно разделить на две области: область с большой вероятностью и область с малой вероятностью. Деление это условно в смысле того, что считать малой, а что большой вероятностью. Ответственность за то, какие значения вероятности считать малыми, а какие большими, берёт на себя стандарт или разработчик нестандартной методики контроля. Та область, вероятность попадания в которую достаточно мала, принимается за критическую область (область CR) и называется «областью отклонения нулевой гипотезы». Действительно, если значение тестовой статистики, полученное по выборке в предположении верности нулевой гипотезы, попадает в критическую область, т.е. в область малых вероятностей, то это, прежде всего, может означать, неверность предположений, сделанных в нулевой гипотезе, которую в этом случае следует отклонить в пользу альтернативной гипотезы Н₁. Значение вероятности, которое соответствует критической области называется «уровнем значимости», а про те значения тестовой статистики, которые попадают в эту область говорят, что они «значимо» отличаются от тех, которые должны быть при верности Н₀.

Однако в критическую область пусть и с малой вероятностью могут попасть значения тестовой статистики и при верности нулевой гипотезы. Следовательно, уровень значимости есть ни что иное, как риск первого рода, т.е. вероятность отклонения верной нулевой гипотезы. Аналогично, если Н₀ не верна, но тестовая статистика тем не менее попадает в область принятия этой гипотезы, и, естественно, ложная нулевая гипотеза принимается, то тем самым совершается ошибка второго рода. При приёмочном контроле качества выборочными методами риском первого рода является вероятность отклонения партии (отказ от поставки её потребителю), если она на самом деле соответствует требованиям к её качеству. Риск второго рода – вероятность принятия партии (поставка потребителю), если она на самом деле не соответствует требованиям к её качеству.

При приёмочном контроле качества имеется более или менее надёжная информация только о части продукции – о выборке, представленной в виде тестовой статистики g(x). О партии в целом в лучшем случае имеется только косвенная информация (например, в виде данных от контрольных карт технологических операций). Возникает вопрос о том, насколько чувствителен тот или иной план контроля к тому, что параметры распределения контролируемого признака качества от партии к партии вдруг «поплыли» (стали непредсказуемым образом изменяться). Ответ на этот вопрос даёт основная характеристика плана выборочного контроля, которая называется «мощность критерия» или тесно связанная с ней функция «оперативной характеристики». Мощность критерия – это вероятность отклонения нулевой гипотезы как функция от параметра q, к которому сведена нулевая гипотеза в параметрической форме. Математически мощность критерия определяется следующим образом:

G(q) = P((g(x) Î CR)ïq) = {Вероятность того, что значение тестовой статистики g(x) попадёт в критическую область CR отклонения Н₀ как функция от контролируемого параметра q}

Таким образом, мощность критерия есть вероятность отклонения партии (попадание тестовой статистики g(x) в критическую область) в зависимости от конкретного значения параметра q. Если для принятия Н₀ требуется выполнение соотношения q = q₀, то для мощности критерия должно выполняться равенство:

G(q = q₀) = a,

где a – заданное значение риска первого рода.

Обобщая это соотношение на все возможные значения параметра q, можно сделать вывод, что в общем случае мощность критерия есть по сути дела функция риска первого рода от контролируемого в рамках нулевой гипотезы параметра q.

Поскольку, по определению G(q) есть вероятность отклонения партии, то альтернативная к ней вероятность принятия партии определяется соотношением:

L(q) = 1 - G(q) = P((g(x) Ï CR)ïq) = {Вероятность того, что значение тестовой статистики g(x) не попадёт в критическую область CR отклонения Н₀ как функция от параметра q}

Функция L(q) называется функцией оперативной характеристики. Естественно, при q = q₀ должно выполняться L(q = q₀) = b, и вообще, оперативная характеристика есть функция ошибки второго рода от контролируемого в рамках нулевой гипотезы параметра q.

Из определения функций L(q) и G(q) видно, что при любом одном и том же значении параметра q, они связаны между собой простым соотношением:

L(q) + G(q) = 1

или a(q) + b(q) = 1.

При приёмочном контроле качества риски первого и второго рода назначаются при разных значениях q. В этом случае:

a(q = q₀) + b(q =q₁) ¹ 1,

где q₀ – значение параметра q, при котором риск первого рода должен быть не менее заданного значения a;

q₁ – значение параметра q, при котором риск второго рода (вероятность принятия не верной нулевой гипотезы) должен быть не более установленного значения b.

В качестве примера рассмотрим случай проверки автомата по дозированию жидкости, описанный в разделе «Статистика» курса «Теория вероятностей и математическая статистика». Этот пример будем рассматривать с точки зрения контроля качества автомата по параметру точности дозировки у.

Изготовитель (поставщик) автоматов договаривается с покупателем (потребителем) о том, что поставке подлежат только такие автоматы, у которых математическое ожидание дозы составляет m_у = 0,5 л, при этом вероятность поставки автомата с m_у = 0,48 л должна быть не более 0,01 (b(m_у = 0,48) ≤ 0,01). На основе анализа технологических возможностей производства «высокие договаривающиеся стороны» принимают к сведению, что показатель качества – индивидуальная доза, имеет нормальный закон распределения со стабильной и известной дисперсией s = 0,02 л. (случай m = var, s = const см. раздел 2.2). Поскольку, показатель качества не сводится к доле несоответствующих изделий (автоматов), то поставщик не может воспользоваться стандартным планом выборочного контроля и вынужден самостоятельно разработать надёжную методику контроля с учётом как интересов потребителя (риска потребителя b), так и собственных интересов (собственного риска a, т.е. риска забраковать годный (исправный) автомат). В терминах проверки статистических гипотез задача ставится следующим образом:

Разработать критерий проверки (план выборочного контроля) нулевой гипотезы Н₀:{m = m₀} против альтернативной Н₁:{m < m₀}. Причём риск отклонить Н₀, когда она верна, т.е. при m ≥ m₀, должен быть не более a (например, a = 0,05). Риск принять Н₀ при m = m₁, должен быть не более b = 0,01. В качестве тестовой статистики естественно принять выборочное среднее =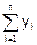нескольких контрольных доз. Требуется определить такой план выборочного контроля (найти объём выборки n и критическое значение у_кр), который обеспечит выполнение рисков потребителя b и поставщика a.

Решение:

1) условие обеспечения рисков поставщика и потребителя означает, что оперативная характеристика плана контроля должна проходить не ниже точки (m = m₀, 1 - a) и не выше точки ((m = m₁, b). Для первой точки: вероятность отклонения партии при m = m₀ должна быть не более a = 0,05 или, соответственно, вероятность приёмки не менее 1-a = 0,95; для второй точки – вероятность приёмки партии при m = m₁ должна быть не более b = 0,01;

2) учитывая, что выборочное среднее из нормально распределённой генеральной совокупности так же распределено нормально с параметрами (m; s²/n), выражение для оперативной характеристики будет следующим:

L(m) = P( Ï CR ïm) = P( ≥ у_крïm) = 1 – ; (3.2)

3) для m = m₀ и m = m₁ должны выполняться соотношения:

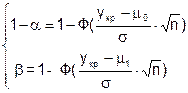
или, переходя к квантилям:

(3.3)

т.е. получаем систему двух уравнений с двумя неизвестными у_кр и n, которые легко определяются:

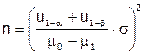и у_кр = 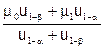(3.4)

4) подставляя в полученные соотношения исходные параметры m₀ = 0,5, m₁ = 0,48, a = 0,05, b = 0,01, получим:

= 15,76» 16; (3.5)

у_кр = = 0,4917; (3.6)

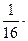
5) методика контроля сводится к получению 16-ти контрольных доз и вычислению выборочного среднего =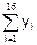, где y_i – i-я контрольная доза (i=1,2,…,16);

6) правило принятия решения следующее:

если среднее 16-ти контрольных доз будет больше или равно y_кр = 0,4917, то автомат соответствует требованиям по точности дозы и его можно поставлять потребителю;

если среднее 16-ти контрольных доз будет меньше y_кр = 0,4917, то автомат не соответствует требованиям по точности дозы и его нельзя поставлять потребителю;

7) ОХ полученного плана выборочного контроля можно построить по формуле (3.2) для любых m, подставив вместо y_кр и n, рассчитанные по (3.5) и (3.6) значения:

L(m) = P( ≥ у_крïm) = 1 – ==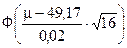 Ф[(m - 0,4917)×200).

График оперативной характеристики представлен на рис. 3.2.

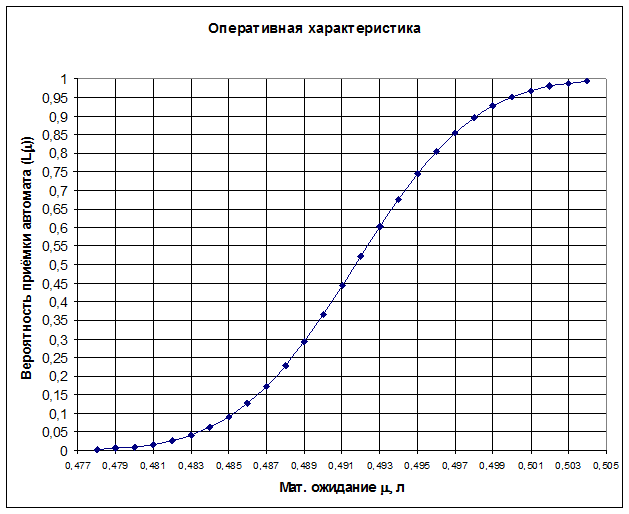
Рисунок 3.2

Обратить внимание на 3 момента:

1) при определении объёма выборки по (3.5) округление следует выполнять до большего целого числа (Почему?);

2) при вычислении у_кр следует пользоваться формулой (3.4), хотя при расчёте по любой из формул (3.3) и использовании дробного значения n (без округления) должны получаться те же значения у_кр, что и по (3.4) (Докажите это);

3) по точкам на оси ординат графика ОХ можно определить как вероятность приёмки партии для любого значения m, так и вероятность браковки (отклонения) партии (Представьте схематично, как будет выглядеть график мощности критерия данного плана контроля).

Дата добавления: 2014-01-15