
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Спеціальні бінарні відношення
Нехай 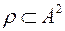 ,
, 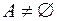 .
.
Означення. Відношенням еквівалентності називається бінарне відношення 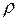 на множині
на множині , якщо воно рефлексивне, симетричне і транзитивне, тобто:
, якщо воно рефлексивне, симетричне і транзитивне, тобто:
1) 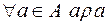 ;
;
2) 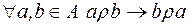 ;
;
3) 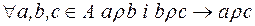 .
.
Відношення еквівалентності є узагальненням відношення = на між числами або множинами. Часто позначається спеціальним символом 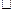 .
.
Приклади:
1. Відношення рівності на будь-якій числовій множині.
2. Відношення подібності на множині плоских трикутників.
3. Відношення ‘‘мати ту саму остачу від ділення на 7’’ на множині  .
.
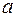 множини
множини  називається множина всіх елементів множини
називається множина всіх елементів множини  , які еквівалентні
, які еквівалентні 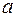 . Позначається
. Позначається  .
. 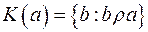 . Приклад. 1. Відношення рівності на множині
. Приклад. 1. Відношення рівності на множині  породжує наступні класи еквівалентності: для будь-якого
породжує наступні класи еквівалентності: для будь-якого 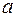
 , тобто кожен клас еквівалентності складається з одного елемента.2. Клас еквівалентності, породжений парою цілих чисел
, тобто кожен клас еквівалентності складається з одного елемента.2. Клас еквівалентності, породжений парою цілих чисел  , який задається співвідношенням
, який задається співвідношенням  , визначає одне раціональне число. Означення. Розбиттям непорожньої множини
, визначає одне раціональне число. Означення. Розбиттям непорожньої множини  називається сукупність таких її непорожніх підмножин
називається сукупність таких її непорожніх підмножин 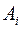 , які не перерізаються (
, які не перерізаються (  ), а в об’єднанні складають всю множину
), а в об’єднанні складають всю множину  (
(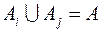 ). Приклад. 1.
). Приклад. 1. 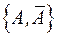 – розбиття універсуму.2.
– розбиття універсуму.2.  – розбиття універсуму.3.
– розбиття універсуму.3. 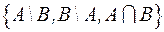 – розбиття множини
– розбиття множини  .Розбиття визначається однозначно і частини розбиття породжують особливий вид відношень, які поводять себе так, як відношення "=" між числами або множинами, тобто розбиття породжує відношення еквівалентності.Має місце Теорема. Сукупність всіх класів еквівалентності є розбиттям множини
.Розбиття визначається однозначно і частини розбиття породжують особливий вид відношень, які поводять себе так, як відношення "=" між числами або множинами, тобто розбиття породжує відношення еквівалентності.Має місце Теорема. Сукупність всіх класів еквівалентності є розбиттям множини  . Справедливе і обернене: Нехай
. Справедливе і обернене: Нехай 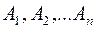 – довільне розбиття множини
– довільне розбиття множини  і для будь-яких елементів
і для будь-яких елементів 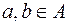 задане бінарне відношення
задане бінарне відношення  належать одному й тому ж класу розбиття. Тоді
належать одному й тому ж класу розбиття. Тоді 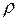 є відношенням еквівалентності. Означення. Множина всіх класів еквівалентності деякої множини
є відношенням еквівалентності. Означення. Множина всіх класів еквівалентності деякої множини  , утворених за відношенням еквівалентності
, утворених за відношенням еквівалентності 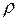 , називається фактормножиною множини
, називається фактормножиною множини  за даним відношенням еквівалентності. Позначається
за даним відношенням еквівалентності. Позначається 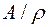 . Фактормножина
. Фактормножина 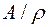 визначає розбиття множини
визначає розбиття множини  на підмножини, які попарно не перерізаються – на класи еквівалентності.З поняття рівності між числами випливає більш широке поняття відношення еквівалентності на множинах. За аналогією нерівності також можуть бути використані як моделі для більш широкого класу відношень – відношень порядку на множинах.
на підмножини, які попарно не перерізаються – на класи еквівалентності.З поняття рівності між числами випливає більш широке поняття відношення еквівалентності на множинах. За аналогією нерівності також можуть бути використані як моделі для більш широкого класу відношень – відношень порядку на множинах. Означення. Відношенням нестрогого порядку називається бінарне відношення 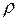 на множині
на множині , якщо воно рефлексивне, антисиметричне і транзитивне, тобто:
, якщо воно рефлексивне, антисиметричне і транзитивне, тобто:
1) 
2)  ;
;
3) 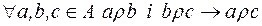 .
.
Відношення нестрогого порядку часто позначається спеціальним символом 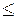 .
.
Означення. Відношенням строгого порядку називається бінарне відношення 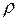 на множині
на множині , якщо воно антирефлексивне, асиметричне і транзитивне, тобто
, якщо воно антирефлексивне, асиметричне і транзитивне, тобто
1) 
2)  ;
;
3)  .
.
Відношення строгого порядку часто позначається спеціальним символом 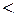 .
.
Означення. Множина  , на якій задане відношення порядку, називається цілком впорядкованою, якщо будь-які два елементи з
, на якій задане відношення порядку, називається цілком впорядкованою, якщо будь-які два елементи з  знаходяться в цьому відношенні і частково впорядкованою в противному випадку.
знаходяться в цьому відношенні і частково впорядкованою в противному випадку.
Приклади:
1. 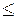 і
і 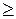 – відношення нестрогого порядку для чисел;
– відношення нестрогого порядку для чисел; 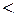 і
і 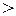 – відношення строгого порядку. Обидва відношення цілком впорядковують множини
– відношення строгого порядку. Обидва відношення цілком впорядковують множини  і
і  .
.
 відношення нестрогого включення
відношення нестрогого включення  задає нестрогий частковий порядок, а відношення строгого включення
задає нестрогий частковий порядок, а відношення строгого включення  задає строгий частковий порядок. Перевіримо властивості відношення нестрогого включення
задає строгий частковий порядок. Перевіримо властивості відношення нестрогого включення  :
: 1) рефлексивність:  ;
;
2) антисиметричність:  ;
;
3) транзитивність:  .
.
Означення. Відношенням лінійного порядку називається зв’язне відношення нестрогого порядку, тобто
1) 
2)  ;
;
3) 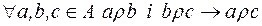 .
.
4) 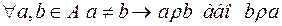 .
.
Означення. Відношенням строгого лінійного порядку називається зв’язне відношення строгого порядку, тобто
1) 
2)  ;
;
3)  .
.
4) 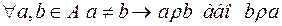 .
.
Означення. Множина  , на якій задане відношення лінійного порядку, називається лінійно впорядкованою.
, на якій задане відношення лінійного порядку, називається лінійно впорядкованою.
Означення. Відношення називається відношенням толерантності, якщо воно рефлексивне, симетричне, але не транзитивне.
Означення. Відношення називається відношенням домінування, якщо воно антирефлексивне, асиметричне і для нього може не виконуватися властивість транзитивності.
|
Дата добавления: 2014-01-11; Просмотров: 1811; Нарушение авторских прав?; Мы поможем в написании вашей работы!