Струны. Формула Даламбера

Тема 4. УРАВНЕНИЕ КОЛЕБАНИЙ БЕСКОНЕЧНОЙ

Найти решение, удовлетворяющее условиям

Задачи для самостоятельного решения.

1. Привести к каноническому виду уравнение

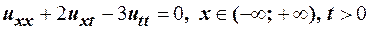
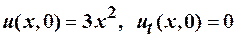
Ответ: .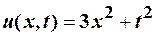

Задача Коши для уравнения колебаний

бесконечной струны. Вывод формулы Даламбера.

Рассмотрим задачу с начальными условиями для неограниченной струны:

, (4.1)

, . (4.2)

Функция задает начальное отклонение струны от положения равновесия, - начальную скорость.

Введём новые переменные: , .

В результате такой замены уравнение приводится к виду

. (4.3)

Интегрируя (4.3) по , получим

,

где - некоторая дифференцируемая функция одной переменной. Интегрируя последнее равенство ещё раз теперь по при фиксированном значении , получим:

. (4.4)

Таким образом, функция , определяемая формулой (4.4), представляет общее решение уравнения (4.3).

Следовательно, функция

(4.5)

является общим интегралом уравнения (4.1).

Определим и таким образом, чтобы удовлетворялись начальные условия:

где и - постоянные. Из полученных равенств находим:

(4.6)

Подставляя в (4.5) найденные значения и , получим:

. (4.7)

Формулу (4.7) называют формулой Даламбера.

Функция , определяемая формулой Даламбера,

представляет процесс распространения начального отклонения и начальной скорости.

Функция описывает полуволну, распространяющуюся вправо, - влево от начального профиля, причём скорости движения этих волн равны параметру .

Выводы: общее решение задачи Коши – это суперпозиция двух волн , одна из которых

распространяется налево со скоростью а, а вторая – направо с той же скоростью. При этом

,

,

где обозначено .

Рассмотрим частные случаи.

1) Допустим, что начальная скорость равна нулю:

.

В этом случае отклонение выразится формулой

(4.8)

и является суммой левой и правой бегущих волн.

Начальная форма каждой волны определяется функцией , равной половине начального отклонения.

2) Допустим, что начальное отклонение равно нулю:

.

В этом случае отклонение выразится формулой

, (4.9)

и представляет возмущение струны, создаваемое начальной скоростью.

Пример 1. Рассмотрим распространение начального отклонения, заданного в виде равнобедренного треугольника. Такой начальный профиль можно получить, если оттянуть струну в середине отрезка .

На рис. 4.1 показаны последовательные положения струны через промежутки времени .

Рис. 4.1.

Задача Коши для неоднородного уравнения

колебаний.

Рассмотрим неоднородное уравнение колебаний струны

, , (4.10)

, , . (4.11)

Используя метод редукции, представим решение в виде

,

Задача А Задача B

Решение задачи можно найти по формуле Даламбера (4.7).

Для нахождения найдем функцию , являющейся решением вспомогательной задачи Коши:

.

Решение вспомогательной задачи Коши можно найти по формуле Даламбера, только если заменить на :

.

Лемма. Решением задачи является функция

.

Доказательство. Очевидно, что .

.

Из этого равенства и условий на функцию следует:

.

Покажем, что удовлетворяет уравнению.

Вычислим вторые частные производные:

.

.

Из полученных соотношений следует, что

.

Лемма доказана.

Подставляя выражения , , окончательно запишем решение задачи Коши для неоднородного волнового уравнения:

(4.12)

Дата добавления: 2014-01-15