
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило знаходження частинних похідних
|
|
|
|
При знаходженні частинної похідної  обчислюють звичайну похідну функції однієї змінної
обчислюють звичайну похідну функції однієї змінної 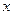 , вважаючи змінну
, вважаючи змінну  сталою, а при знаходженні похідної
сталою, а при знаходженні похідної  сталою вважається змінна
сталою вважається змінна 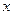 .
.
Тому частинні похідні знаходяться за формулами і правилами обчислень похідних функцій однієї змінної.
Частинна похідна 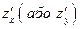 характеризує швидкість зміни функції в напрямі осі
характеризує швидкість зміни функції в напрямі осі 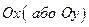 .
.
Геометричний зміст частинної похідної: 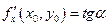 , де
, де 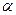 – кут між віссю
– кут між віссю 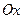 і дотичною, проведеною до кривої
і дотичною, проведеною до кривої  в точці
в точці  .
.
Аналогічно, 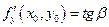 , де
, де  – кут між віссю
– кут між віссю  і дотичною, проведеною до кривої
і дотичною, проведеною до кривої  в точці
в точці  .
.
Для функції 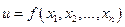 n змінних можна знайти n частинних похідних
n змінних можна знайти n частинних похідних  , де
, де  ,
,
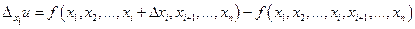 .
.
Щоб знайти частинну похідну 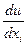 , треба знайти звичайну похідну функції
, треба знайти звичайну похідну функції 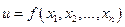 по змінній
по змінній  , вважаючи решту змінних сталими.
, вважаючи решту змінних сталими.
Якщо існує частинна похідна по змінній 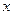 від функції
від функції 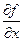 , то її називають частинною похідною другого порядку від функції
, то її називають частинною похідною другого порядку від функції 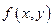 по змінній
по змінній 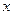 і позначають
і позначають  .
.
Якщо існує частинна похідна по змінній  від функції
від функції 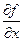 , то її називають мішаною частинною похідною другого порядку від функції
, то її називають мішаною частинною похідною другого порядку від функції 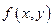 і позначають
і позначають 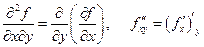 .
.
Для функції двох змінних 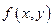 розглядають чотири похідні другого порядку
розглядають чотири похідні другого порядку 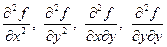 .
.
Якщо існують частинні похідні від частинних похідних другого порядку, то їх називають частинними похідними третього порядку функції 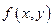 , їх вісім:
, їх вісім:
 .
.
Теорема (про мішані похідні)
Якщо функція 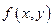 визначена разом зі своїми похідними
визначена разом зі своїми похідними 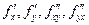 в деякому околі точки
в деякому околі точки 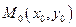 , причому
, причому 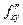 та
та  неперервні в точці
неперервні в точці 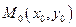 , то в цій точці
, то в цій точці  .
.
Приклад. Знайти частинні похідні першого та другого порядку функції  .
.

3. Диференційовність функції
Нехай функція  визначена в деякому околі точки
визначена в деякому околі точки 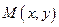 . Виберемо прирости
. Виберемо прирости 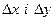 так, щоб точка
так, щоб точка 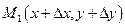 належала розглядуваному околу і знайдемо повний приріст функції в точці
належала розглядуваному околу і знайдемо повний приріст функції в точці 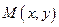 :
:
 .
.
Функція 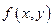 називається диференційовною в точці
називається диференційовною в точці  , якщо її повний приріст в цій точці можна подати у вигляді
, якщо її повний приріст в цій точці можна подати у вигляді
|
|
|
 ,
,
де 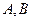 – дійсні числа, які не залежать від
– дійсні числа, які не залежать від  ,
,
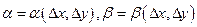 – нескінченно малі функції при
– нескінченно малі функції при 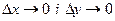 .
.
Властивості функції двох змінних:
Теорема 1 (неперервність диференційовної функції)
Якщо функція  диференційовна в точці
диференційовна в точці  , то вона неперервна в цій точці.
, то вона неперервна в цій точці.
Теорема 2 (існування частинних похідних диференційовної функції)
Якщо функція  диференційовна в точці
диференційовна в точці 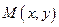 , то вона має в цій точці похідні
, то вона має в цій точці похідні  та
та  і
і 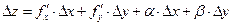 .
.
Теорема 3 (достатні умови диференційовності)
Якщо функція 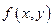 має частинні похідні в деякому околі точки
має частинні похідні в деякому околі точки  і ці похідні неперервні в точці
і ці похідні неперервні в точці  , то функція
, то функція 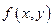 диференційовна в точці
диференційовна в точці  .
.
Наслідок (з теореми 2 і теореми 3)
Щоб функція 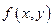 була диференційовною в точці необхідно, щоб вона мала в цій точці частинні похідні і достатньо, щоб вона мала в цій точці неперервні похідні.
була диференційовною в точці необхідно, щоб вона мала в цій точці частинні похідні і достатньо, щоб вона мала в цій точці неперервні похідні.
4. Повний диференціал функції. Диференціали вищих порядків
Якщо функція  диференційовна в точці
диференційовна в точці  , то її повний приріст в цій точці можна подати у вигляді:
, то її повний приріст в цій точці можна подати у вигляді:  , де
, де 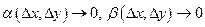 при
при  .
.
Повним диференціалом  диференційовною в точці
диференційовною в точці  функції
функції  називається лінійна відносно
називається лінійна відносно  та
та  частина повного приросту цієї функції в точці
частина повного приросту цієї функції в точці  , тобто
, тобто 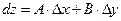 .
.
Диференціалами незалежних змінних 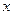 та
та  назвемо прирости цих змінних
назвемо прирости цих змінних  , тоді повний диференціал можна записати:
, тоді повний диференціал можна записати:

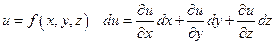
Приклад 1. Знайти повний диференціал функції  .
.

Повний диференціал функції  називають диференціалом першого порядку.
називають диференціалом першого порядку.
Диференціал другого порядку визначають за формулою  .
.
Тоді, якщо функція 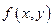 має неперервні частинні похідні, то
має неперервні частинні похідні, то
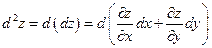 або
або 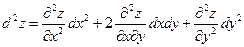 .
.
Символічно це записують  .
.
Диференціал третього порядку  .
.
Диференціал  порядку
порядку 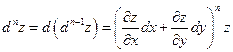 .
.
Приклад 2. Знайти диференціал другого порядку функції  .
.

5. Похідна складеної функції. Повна похідна
Нехай  – функція двох змінних
– функція двох змінних 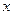 та
та  , кожна з яких, в свою чергу, є функцією незалежної змінної
, кожна з яких, в свою чергу, є функцією незалежної змінної  :
:  , тоді функція
, тоді функція  є складеною функцією змінної
є складеною функцією змінної  .
.
|
|
|
Теорема (похідна складеної функції)
Якщо функції  диференційовні в точці
диференційовні в точці  , а функція
, а функція  диференційовна в точці
диференційовна в точці 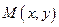 , то складена функція
, то складена функція  також диференційовна в точці
також диференційовна в точці  . Похідну цієї функції знаходять за формулою
. Похідну цієї функції знаходять за формулою 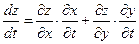 .
.
Якщо  , де
, де  ,то
,то 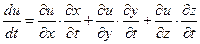 .
.
Якщо  , а
, а 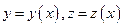 , то
, то 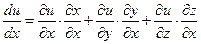 , а оскільки
, а оскільки  , то
, то  – формула для обчислення повної похідної.
– формула для обчислення повної похідної.
Приклад 3. Знайти  функції
функції 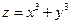 , якщо
, якщо  .
.
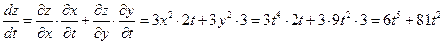
Розглянемо загальний випадок. Нехай  – функція двох змінних
– функція двох змінних 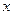 та
та  , які, в свою чергу, залежать від змінних
, які, в свою чергу, залежать від змінних 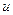 та
та  :
: 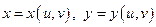 , тоді функція
, тоді функція  є складеною функцією незалежних змінних
є складеною функцією незалежних змінних 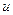 та
та  , а змінні
, а змінні 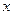 та
та  – проміжні.
– проміжні.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 16782; Нарушение авторских прав?; Мы поможем в написании вашей работы!