Кинематика движения материальной точки по окружности

Плоское движение. Вращательное движение.

Плоским называется движение, при котором траектории точек тела лежат в параллельных плоскостях. Движение тела, в этом случае, полностью определяется движением одного из его сечений в какой либо из параллельных плоскостей (см. рисунок). Частным случаем плоского движения является вращательное движение. При вращательном движении точки тела, находящиеся на прямой, называемой осью вращения — неподвижны. Остальные точки твердого тела движутся по окружностям в плоскостях перпендикулярных оси вращения.

Любое плоское движение можно изобразить в виде суммы (т. е. наложений) двух движений: поступательного движения центра инерции тела и вращательного движения вокруг оси, проходящей через центр инерции нормально плоскостям, в которых происходит вращение точек тела. Примером плоского движения является катящийся по поверхности цилиндр. При вращательном движении все точки движутся по окружностям, поэтому предварительно рассмотрим кинематику движения материальной токи по окружности.

Если материальная точка движется по окружности, то её положение при заданном радиусе окружности вполне определяется углом, φ, который составляет радиус-вектор 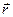, проведённый из центра окружности с осью отсчёта ox. Зависимость 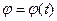полностью задаёт движение материальной точки по окружности радиуса R. Угол поворота φ измеряется в радианной мере.

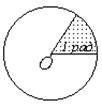
Углом в 1 радиан называют такой центральный угол, длинна дуги которого равна её радиусу. Чтобы узнать угол Δ φ в радианной мере, надо узнать сколько раз радиус R укладывается в дуге окружности Δ S: . Единица измерения радиан не имеет размерности.

Угол в 1 оборот равен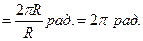

Чтобы определить дугу окружности надо её радиус умножить на центральный угол в радианной мере: .

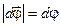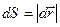Бесконечно малый угол поворота — векторная величина, направленный перпендикулярно плоскости вращения и связан с направлением вращения правовинтовой системой. При этом угол поворота связан с дугой dS и радиусом вращения r соотношением . Учитывая, что , получим 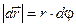. Вектора , , образуют правовинтовую систему, тогда

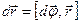. (1)

Быстроту вращения материальной точки по окружности характеризует угловая скорость. Вектор угловой скорости 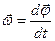направлен в ту же сторону что и , т. е. по оси вращения и связан с вращением правовинтовой системой. Модуль вектора угловой скорости 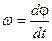, а единица измерения . Разделив обе части уравнения (1) на , получим .

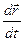— скорость движения материальной точки по траектории (линейная скорость) , направленная по касательной к траектории движения,

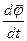— вектор угловой скорости 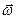. Тогда, . Так как угол между векторам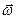и и 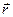равен 90°, то .

Если радиус-вектор 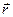проводить не из центра окружности, а из любой точки взятой на оси вращения, то при вращении точки по окружности радиус-вектор 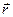будет вращаться по коничкской поверхности, или, как говорят, радиус-вектор 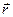будет прецессировать, а уравнение прецессии будет иметь вид:

,

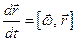где 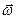— вектор угловой скорости прецессии радиус-вектора .

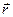Модуль вектора 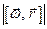равен 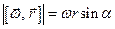, а учитывая, что 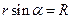, получим что 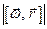это есть модуль линейной скорости материальной точки вращающейся по окружности радиуса.

По уравнению вида , можно судить, что вектор будет прецессировать с угловой скоростью равной вектору .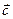

Быстроту изменения угловой скорости 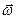характеризует угловое ускорение:

. Представив вектор угловой скорости в ви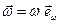де (где — единичный вектор в направлении вектора 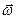), запишем .

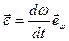Из этого соотношения видно, что вектор углового ускорения 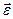сонаправлен с 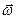, если модуль угловой скорости увеличивается (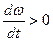) и противоположен 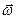, если модуль угловой скорости уменьшается (). Модуль углового ускорения , а единица измерения .

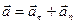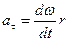Найдём связь ускорения движения материальной точки по траектории с угловыми величинами. Вектор полного ускорения . Тангенциальное ускорение . Учитывая, что , получим или 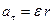. В векторной форме .

Нормальное ускорение. Учитывая, что , получим 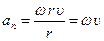, или в векторной форме 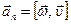. Запишем модуль нормального ускорения только через угловую скорость .

Дата добавления: 2014-01-20