Некоторые свойства z-преобразования

I. Линейность. Есл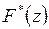и и 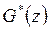, то для любых комплексных постоянных 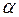и

.

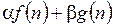
II. Теорема запаздывания (первая теорема смещения).

Если 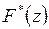, то для любого целого справедливо преобразование

,

III. Теорема опережения (вторая теорема смещения).

Если 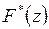, то для любого целого справедливо преобразование

.

IV. Дифференцирование изображения. Справедливо соотношение

,

В частности, .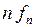

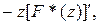
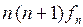
V. Изображение суммы. Если 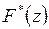, то .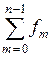

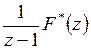VI. Теорема подобия. Если , то справедливо соотношение

, где .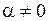

VII. Теорема о свертке оригиналов - последовательностей. Пусть , , 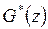тогда справедливо соотношение

.

Для того, чтобы по известному изображению 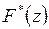найти оригинал можно:

1) воспользоваться таблицей, после разбиения дроби 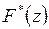на сумму простейших дробей;

2) в случае, когда 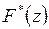есть правильная рациональная дробь относительно 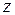, функцию 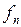можно найти по формуле

,

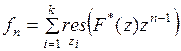где сумма берется по всем полюсам функции .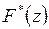

Решение разностных уравнений

Разностью первого порядка решетчатой функции называется величина, обозначаемая как , и равная .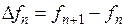

Разностью второго порядка 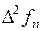называется величина, определяемая как .

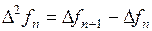Разностью 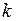-го порядка называется величина

.

, где .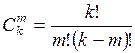

Теорема (о 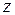-преобразовании разности). Пусть 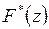. Тогда 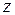-преобразование разностей равны

,

.

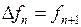
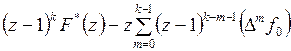Р азностным уравнением 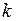-го порядка называется уравнение вида

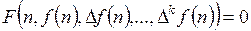
или

,

где – решетчатая функция.

Рассмотрим процедуру решения линейного неоднородного разностного уравнения:

.

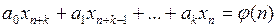1) Применяем к обеим частям уравнения дискретное преобразование Лапласа

,

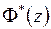
и, учитывая, что

,

,

...

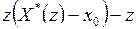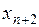
получим линейное алгебраическое уравнение относительно изображения .

2) Разрешив полученное уравнение относительно , возвращаемся назад к оригиналу – последовательности. Общее решение будет содержать неопределенные константы , которые фиксируются, исходя из начальных условий.

Задания к разделу 14.

Пользуясь определением, найти изображение 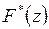для следующих функций:

14.1.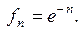

14.2. .

14.3.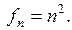

Используя свойства дискретного преобразования Лапласа, найти изображения следующих функций:

14.4.

14.5.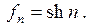

14.6.

14.7.

Пользуясь теоремой об изображении суммы, найти сумму:

14.8.

14.9.

Найти оригиналы для следующих изображений:

14.10.

14.11.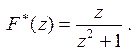

С помощью дискретного преобразования Лапласа решить линейные разностные уравнения:

14.12.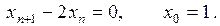

14.13.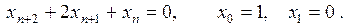

14.14.

14.15.

14.16.

14.17.

14.18.

РАЗДЕЛ 15. Вариационное исчисление

Если каждой функции 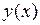из некоторого множества поставлено в соответствие некоторое число J, то говорят, что на этом множестве задан функционал .

Приведем примеры функционалов.

1. Длина плоской кривой, заданной уравнением , :

.

2. Стоимость проезда по дорогам, имеющим вид кривых, соединяющих пункты А и В.

Основная задача вариационного исчисления – исследование функционалов на экстремум и отыскание тех функций, на которых этот экстремум достигается, например:

1. Из всех кривых плоскости, соединяющих точки А и В, найти ту, которая имеет наименьшую длину.

2. Из всех линий найти ту, по которой материальная точка быстрее всего соскальзывает под действием силы тяжести из точки А в точку В (задача о брахистохроне).

Простейшая задача вариационного исчисления

Рассмотрим функционал

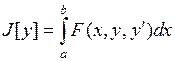, (1)

где – дважды непрерывно дифференцируемая функция.

Граничные точки допустимых кривых будем считать закрепленными:

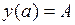, . (2)

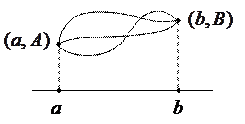Простейшая задача вариационного исчисления ставится так: среди всех функций 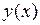(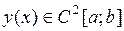) и удовлетворяющих условиям (2), найти ту, которая доставляет экстремум функционалу (1). Эта кривая удовлетворяет уравнению Эйлера

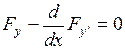(3)

Здесь ; .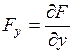

Решения (интегральные кривые) уравнения Эйлера называются экстремалями.

Итак, граничная задача, которой должна удовлетворять функция 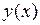, доставляющая экстремум функционалу (1) с граничными условиями (2) выглядит следующим образом:

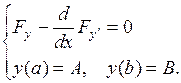(4)

Данная краевая задача может иметь единственное решение, может иметь множество решений или не иметь ни одного.

Частные случаи уравнения Эйлера.

1. F не зависит от : .

Уравнение Эйлера (3) в этом случае принимает вид:

.

Это уравнение является алгебраическим и определяет одну или конечное число кривых, которые могут и не удовлетворять граничным условиям.

2. F зависит лишь от : .

В этом случае экстремалями является семейство прямых линий

,

где 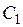и – произвольные постоянные, определяемые из граничных условий (2).

Задания к разделу 15.

В следующих примерах найти расстояния между данными кривыми на указанных интервалах.

15.1.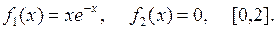

15.2.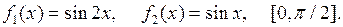

15.3.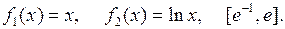

Найти экстремали следующих функционалов:

15.4.

15.5. ; ; .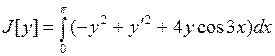

15.6. ; ; .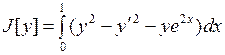

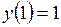15.7. ; ; .

15.8. ; ; .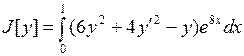

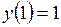15.9.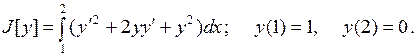

15.10.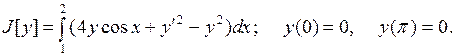

15.11.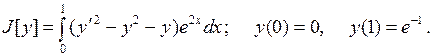

15.12.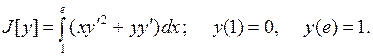

15.13.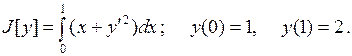

15.14.

15.15.

15.16.

15.17. Задача о положении равновесия тяжелой однородной нити под действием силы тяжести. Среди всех плоских линий длины , концы которых лежат в заданных точках 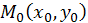и , найти ту, у которой ордината центра тяжести минимальна.

Найти экстремали в следующих изопериметрических задачах.

15.18.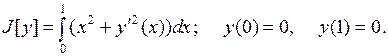

при условии

15.19. Найти минимум интеграла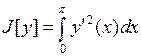

при условии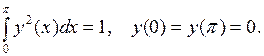

15.20. Найти кратчайшее расстояние между точками и , лежащими на поверхности .

15.21. Найти расстояние между параболой и прямой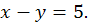

15.22. Найти расстояние от точки 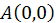до кривой y.

15.23. Найти кратчайшее расстояние от точки до эллипса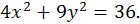

15.24. Найти кратчайшее расстояние от точки до параболы

15.25. Найти кратчайшее расстояние от точки до поверхности

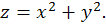
ЛИТЕРАТУРА

1. Специальные математические методы и функции: учебно-методическое пособие по одноименной дисциплине для студентов специальности 1-36 04 02 «Промышленная электроника» днев. и заоч. форм обучения./ А. А. Бабич, Л. Д. Корсун, А. В. Емелин. - Гомель: ГГТУ им. П. О. Сухого, 2010. - 195 с.

2. Методические указания к контрольным заданиям по курсу «Специальные математические методы и функции» для студентов заочной формы обучения специальности 1-36 04 02 «Промышленная электроника»/ А. А. Бабич, Л. Д. Корсун, А. В. Емелин. - Гомель: ГГТУ им. П. О. Сухого, 2011. - 53 с.

3. Деч, Г. Руководство к практическому применению преобразования Лапласа и z-преобразования/ Г. Деч. - Москва: Наука, 1971. - 288 с.

4. Краснов, М.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Учеб. пособие для втузов./ М.Л. Краснов, А.И. Киселев, Г.И. Макаренко - М.: Наука, 1981. – 302с.

5. Краснов, М.Л. Сборник задач по обыкновенным дифференциальным уравнениям: Учеб. пособие для втузов./ М.Л. Краснов, А.И. Киселев, Г.И. Макаренко - М.: Наука, 1981.

6. Ефимов, А. В. Сборник задач по математике для втузов.: Учебное пособие. / В. А. Болгов, А. В. Ефимов, А. Ф. Каракулин и др./ под ред. А.В. Ефимова и Б.П. Демидовича. – Москва: Наука, 1986. - Ч.2. Специальные разделы математического анализа. – 386 с.

7. Ефимов, А. В. Сборник задач по математике для втузов.: Учебное пособие/ Э. А. Вуколов, А. В. Ефимов, В. Н. Земсков и др./ под. Ред. А.В. Ефимова. - Москва: Наука, 1990. - Ч.4. Методы оптимизации. Уравнения в частных производных. Интегральные уравнения – 304 с.

8. Коллатц, Л. Задачи на собственные значения с техническими приложениями./ Л. Коллатц. – Москва: Наука, 1968. - 504 с.

Дата добавления: 2014-01-20