Использование пределов для сравнения порядка роста двух функций

Несмотря на то что без строгих определений множеств О, Q, W нельзя обойтись при доказательстве их абстрактных свойств, они редко используются при сравнении порядков роста двух конкретных функций. Дело в том, что существует более удобный метод выполнения этой оценки, основанный на вычислении предела отношения двух рассматриваемых функций. Может существовать три основных

случая:

Для двух первых случаев для двух последних а для второго 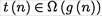. Методы основанные на вычислении пределов более удобны, чем рассмотренные выше, основанные на определении множеств. При рассмотрении след. примеров будем пользоваться правилом Лопиталя 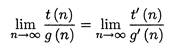и формулой Стирлинга

Пример 1. Сравните порядки роста функций n(n - 1)/2 и n².

Поскольку предел равен положительной константе, обе функции имеют одинаковый порядок роста, что записывается как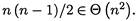

Пример 2. Сравните порядки роста функций log₂n и .

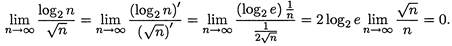
Поскольку предел равен нулю, функция log₂n имеет меньший порядок роста, чем . (Так как 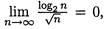, то для этого случая можно использовать так называемую форму записи "с маленькой о": . В отличие от прописной греческой "О" при анализе алгоритмов строчная "о" используется довольно редко.)

Пример 3. Сравните порядки роста функций n! и 2ⁿ. Воспользовавшись формулой Стирлинга, получим:

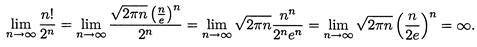
Следовательно, хотя функция 2ⁿ растет очень быстро, функция n! растет еще быстрее, что записывается так: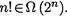

Основные классы эффективности.

Хотя в основах анализа алгоритмов к одному классу относят все функции, чей порядок роста одинаков с точностью до постоянного множителя, существует бесконечное множество подобных классов. Например, порядок роста показательной функции аⁿ зависит от значения основания а. Поэтому временную эффективность большого количества алгоритмов можно отнести всего к нескольким классам. Эти классы, их названия, а также некоторые пояснения, приведены в таблице в соответствии с возрастанием их порядка роста.

Дата добавления: 2014-01-20