Линеаризация уравнений, нелинейных относительно факторных переменных

Нелинейные относительно оцениваемых параметров

y=a₀ x^a1 (степенная)

y=a₀ a₁^x (показательная)

y=e^a0+a1*x(экспоненциальная)

Первый класс функций обычно сводится к уравнениям множественной линейной регрессии путем замены переменных.

Например, рассмотрим расчет параметров следующего уравнения:

y=a₀ + a₁x + a₂x² (уравнение парной квадратической регрессии или просто параболы).

Обозначим x=x₁; x²=x₂

И получим уравнение линейной двухфакторной регрессии y=a₀ + a₁x₁+ a₂x_2, для которого ранее (в лекции №10) уже была рассмотрена система нормальных уравнений.

Система уравнений для расчета параметров двухфакторной линейной регрессии y=a₀ + a₁x₁+ a₂x₂ имеет вид:

a₀n+ a₁ ∑x₁+a₂ ∑x₂=∑y

a₀∑x₁ + a₁ ∑x²₁+a₂ ∑x₁x₂=∑yx₁ (11.1)

a₀∑x₂+ a₁ ∑x₁x₂+a₂∑x₂² =∑yx₂

Если в системе (1) выполнить обратную замену переменных (заменить x₁ на x, а x₂ на x²) то мы получим систему (2) для расчета параметров уравнения парной квадратической регрессии y=a₀ + a₁x + a₂x²

a₀n+ a₁ ∑x+a₂ ∑x²=∑y

a₀∑x_n + a₁ ∑x²+a₂ ∑x³=∑yx (11.2)

a₀∑x²+ a₁ ∑x³+a₂∑x⁴ =∑yx²

Точно так же можно определить системы нормальных уравнений для других нелинейных зависимостей. Например, построим систему нормальных уравнений для расчета параметров гиперболы y= a₀ + a₁/x

Выполняя замену переменных 1/x=z, получаем обычное линейное уравнение y=a₀+a₁z и соответствующую ему систему нормальных уравнений:

a₀+a₁Σz=Σy

a₀Σz+a₂Σz²=Σyz (11.3)

Подставляя в систему (11.3) вместо z переменную 1/x получаем систему (11.4) нормальных уравнений для расчета параметров гиперболы:

na₀+a₁∑1/x=∑y

a₀∑1/x+a₁∑1/x²=∑y/x (11.4)

Такое уравнение регрессии (в виде гиперболы) часто используется для описания различных экономических процессов, например, если a₂>0, то классическим примером такой зависимости будет так называемая кривая Филлипса.

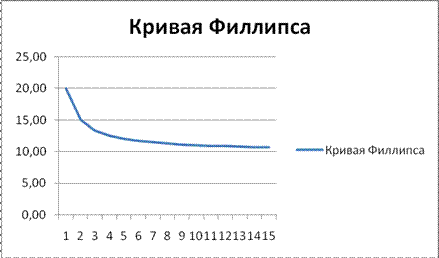
В конце 50-х ХХ в. английский экономист Филлипс установил (на основе статистики за 100 лет) такую (обратную) зависимость между уровнем безработицы и приростом средней заработной платы.

Если a₂<0, то гипербола имеет вид:

Такая кривая известна в экономической теории под названием «Кривая Энгеля». Такой зависимостью хорошо описывается взаимосвязь между долей расходов и покупку товаров длительного пользования в общей сумме потребительских расходов и величиной доходов населения.

Эту закономерность вывел в 1857 году немецкий статистик Э.Энгель.

Для описания “кривой Энгеля”, т.е. монотонно возрастающей функциис заданным пределом насыщения, может использоваться не только гипербола. Экономисты Уоркинг (1943г.) и Лизер (1964г.) использовали для описания “кривой Энгеля” полулогарифмическую функцию y= a₀+a₁ln x.

Чтобы рассчитать параметры такого уравнения регрессии, строится система:

na₀+a₁∑ln x =∑y

a₀∑ln x +a₁∑(ln x)² =∑y ln x (11.5)

Линеаризация второго класса функций (нелинейных по оцениваемым параметрам).

Второй класс функций приводится к линейному виду путём специальных процедур линеаризации. Наиболее часто используют логарифмирование.

Однако эта процедура применима не ко всем функциям.

Некоторые уравнения (которые в эконометрике называют нелинейными, но внутренне линейными уравнениями) легко приводятся к линейному виду путём логарифмирования.

Например, рассмотрим уравнение степенной функции y=a₀ x^a₁

Логарифмируя, получаем ln y = ln a₀ + a₁ ln x

Затем заменяем переменные:

y₁=ln y

x₁= ln x

y₁ = ln a₀ + a₁ x₁

Пользуясь методом наименьших квадартов, находим параметры этого уравнения, т.е. ln a₀ и a₁

Затем рассчитываем параметр a₀ = e^{ln a0}

При использовании таких процедур линеаризации, которые затрагивают преобразование зависимой переменной, необходимо проверять выполнение предпосылок метода наименьших квадратов (МНК), так как они могут нарушаться при преобразовании.

Например, для линейных уравнений регрессии обычно выполняется S (y – y_x)=0 – это одна из предпосылок МНК. Иными словами, сумма отклонений фактических значений у от расчётных, равна 0.

Напомним, что расчётные значения y_x - это те, которые рассчитаны по уже построенному уравнению регрессии, т.е. y_x =a₀ + a₁x

В нелинейных уравнениях регрессии эта сумма может отличаться от 0, так как после логарифмирования мы применяем МНК к логарифмам переменных, то есть должно соблюдаться условие:

å(ln y – ln y_x) =0, но при этом вообще говоря S (y – y_x) ¹ 0

Это будет нарушением одной из предпосылок, на которых основано использование МНК.

Поэтому при построении нелинейных уравнений регрессии обычно осуществляют последующую проверку исходных предпосылок МНК. Более подробно процедуры, используемые для такой проверки, изучаются в дисциплине «Эконометрика».

Дата добавления: 2014-01-20