Кинематическое уравнение движения материальной точки

Системы отсчета

Для описания движения тел в зависимости от условий конкретных задач используют разные физические модели. Простейшей моделью является материальная точка – тело, массой и размерами которого в условиях данной задачи можно пренебречь. Вопрос о том, можно ли данное конкретное тело рассматривать как материальную точку, зависит не от размеров тела, а от условий задачи. Например, изучая движение Земли по орбите вокруг Солнца, можно считать ее материальной точкой, но нельзя делать этого в задачах о движении тел по ее поверхности.

Положение материальной точки в пространстве определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. Однако движение тел происходит не только в пространстве, но и во времени. Поэтому для описания движения необходимо определять время. Совокупность тел отсчета и отсчитывающих время часов образует систему отсчета.

Для количественного описания движения с системой отсчета связывают систему координат (начало координат, как правило, помещают в тело отсчета). Простейшая прямоугольная система координат – декартова. В декартовой системе координат положение точки А можно определить, задав числа 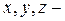декартовы координаты точки – или вектор – радиус-вектор точки А (рис. 1.1.1).

Радиус-вектор связан с декартовыми координатами соотношением:

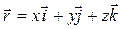, (1.1.1)

где 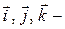единичные векторы прямоугольной системы координат.

Модуль (численное значение) радиуса-вектора равен:

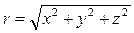. (1.1.2)

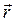При движении материальной точки ее координаты и радиус-вектор изменяются с течением времени. Поэтому для описания движения необходимо указать вид функциональной зависимости всех трех ее координат от времени:

(1.1.3)

либо зависимость от времени радиуса-вектора точки:

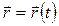. (1.1.4)

Три скалярных уравнения 1.1.3 или эквивалентное им векторное уравнение 1.1.4 называют кинематическим уравнением движения материальной точки.

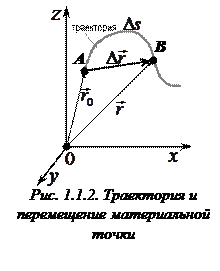Траекторией материальной точки называют линию, описываемую в пространстве точкой при ее движении. В зависимости от формы траектории, различают прямолинейное и криволинейное движение.

Рассмотрим движение материальной точки вдоль произвольной траектории (рис.1.1.2). Отсчет времени начнем с момента, когда точка находилась в положении А. Пусть материальная точка переместилась из положения А в положение В. Расстояние между точками А и В, отсчитанное вдоль траектории, называется длиной пути и является скалярной функцией времени.

Рисунок 1.2.

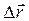Вектор , проведенный из начального положения движущейся точки в её положение в данный момент времени, называется перемещением. Перемещение равно приращению радиуса-вектора движущейся точки. Т.е., если начальное положение точки характеризуется радиусом-вектором , а конечное 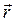, то: .

Длина пути – величина скалярная и неотрицательная, а потому ее нельзя сравнивать с перемещением 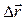, представляющим собой вектор. Сравнивать можно только и модуль перемещения 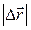. Очевидно, что 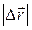. Только при прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения 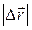равен пройденному пути .

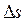Пример 1.1.1. Мотоциклист проехал треть окружности кольцевого трека радиусом . Каковы длина пройденного пути и модуль перемещения мотоциклиста?

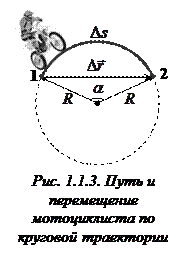Дано: Решение:

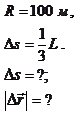Поскольку длина дуги окружности 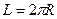, то .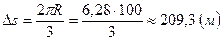

Модуль перемещения мотоциклиста из точки 1 в точку 2 (рис. 1.1.3) найдем из треугольника, образованного радиусами окружности 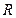и вектором перемещения 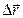. По теореме косинусов, с учетом того, что , получим .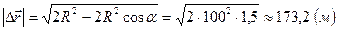

Ответ: , .

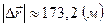Дата добавления: 2014-01-20