
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорение и его составляющие
|
|
|
|
Чаще всего приходится иметь дело с движением, в котором вектор скорости не остается постоянным, а меняется как по модулю, так и по направлению.
Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Пусть вектор 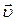 задает скорость материальной точки в положении А в момент времени
задает скорость материальной точки в положении А в момент времени 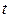 . За время
. За время 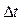 движущаяся точка перешла в положение B и приобрела скорость
движущаяся точка перешла в положение B и приобрела скорость 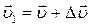 , отличающуюся от
, отличающуюся от 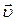 как по модулю, так и по направлению (рис. 1.3.1). Перенесем вектор
как по модулю, так и по направлению (рис. 1.3.1). Перенесем вектор 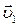 в точку А и найдем вектор изменения скорости
в точку А и найдем вектор изменения скорости  .
.
 Средним ускорением неравномерного движения называется векторная величина, равная отношению изменения скорости
Средним ускорением неравномерного движения называется векторная величина, равная отношению изменения скорости  к тому интервалу времени, за который это изменение произошло:
к тому интервалу времени, за который это изменение произошло:
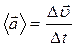 . (1.3.1)
. (1.3.1)
Вектор 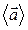 совпадает по направлению с вектором изменения скорости.
совпадает по направлению с вектором изменения скорости.
Мгновенным ускорением называется величина, равная пределу, к которому стремится среднее ускорение материальной точки:
 . (1.3.2)
. (1.3.2)
Таким образом, мгновенное ускорение – векторная величина, равная первой производной скорости по времени.

Пример 1.3.1. Уравнение движения точки по прямой имеет вид: 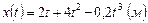 . Найти: 1) среднюю путевую скорость за промежуток времени от
. Найти: 1) среднюю путевую скорость за промежуток времени от 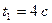 до
до  ; 2) мгновенную скорость и модуль мгновенной скорости в указанные моменты времени; 3) среднее ускорение за промежуток времени от
; 2) мгновенную скорость и модуль мгновенной скорости в указанные моменты времени; 3) среднее ускорение за промежуток времени от 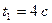 до
до  ; 4) мгновенное ускорение и модуль мгновенного ускорения в указанные моменты времени.
; 4) мгновенное ускорение и модуль мгновенного ускорения в указанные моменты времени.

 Решение:
Решение:
1)  Средняя путевая скорость находится по формуле 1.2.2:
Средняя путевая скорость находится по формуле 1.2.2:
 .
.
Найдем положения движущейся точки в указанные моменты времени:  (м),
(м),
 (м).
(м).
Тогда 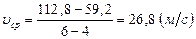 .
.
2) При прямолинейном движении мгновенная скорость в любой момент времени (формула 1.2.4): 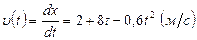 .
.
Модуль мгновенной скорости в указанные моменты времени:
|
|
|
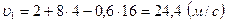 ,
, 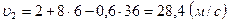 .
.
3) Модуль среднего ускорения (формула 1.3.1):
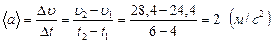 .
.
4) Мгновенное ускорение в любой момент времени (формула 1.3.2):
 .
.
Модуль мгновенного ускорения в указанные моменты времени:
 ,
, 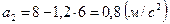 .
.
Ответ: 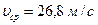 ,
, 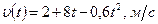 ,
,  ,
, 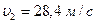 ,
, 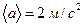 ,
,  ,
, 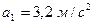 ,
, 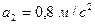 .
.

Разложим вектор изменения скорости  на две составляющие: вдоль направления мгновенной скорости
на две составляющие: вдоль направления мгновенной скорости  и перпендикулярно этому направлению
и перпендикулярно этому направлению  , то есть по касательной к траектории движения и нормали к траектории:
, то есть по касательной к траектории движения и нормали к траектории:
 .
.
Тогда 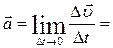
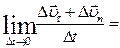
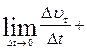
 ,
,
где вектор 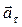 направлен по касательной к траектории, характеризует быстроту изменения скорости по модулю и называется тангенциальным ускорением; вектор
направлен по касательной к траектории, характеризует быстроту изменения скорости по модулю и называется тангенциальным ускорением; вектор  направлен к центру кривизны траектории, характеризует быстроту изменения скорости по направлению и называется нормальным ускорением.
направлен к центру кривизны траектории, характеризует быстроту изменения скорости по направлению и называется нормальным ускорением.
Численные значения тангенциального и нормального ускорений соответственно равны:
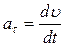 ,
, 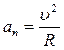 , (1.3.3)
, (1.3.3)
где 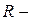 радиус окружности, которая в окрестности данной точки совпадает с траекторией.
радиус окружности, которая в окрестности данной точки совпадает с траекторией.
Мгновенное ускорение 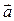 также называют полным ускорением. Численное значение полного ускорения:
также называют полным ускорением. Численное значение полного ускорения:
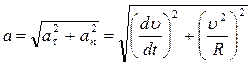 . (1.3.4)
. (1.3.4)
Зная зависимость ускорения от времени 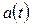 , можно найти зависимость скорости от времени
, можно найти зависимость скорости от времени
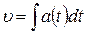 .
.

Пример 1.3.2. Машина идет по закругленному шоссе. Зависимость радиуса-вектора от времени задана уравнением: 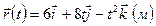 . Найти:1) мгновенную скорость машины и значение скорости в момент времени
. Найти:1) мгновенную скорость машины и значение скорости в момент времени 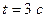 ; 2) тангенциальное и нормальное ускорение в указанный момент времени; 3) радиус кривизны шоссе.
; 2) тангенциальное и нормальное ускорение в указанный момент времени; 3) радиус кривизны шоссе.
 Дано: Решение:
Дано: Решение:
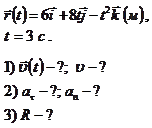 1) Мгновенная скорость
1) Мгновенная скорость 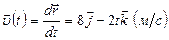 .
.
 Учитывая, что
Учитывая, что 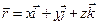 , а
, а 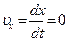 ;
; 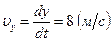 ;
; 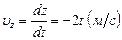 и
и 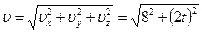 , подставив
, подставив 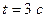 , получим значение скорости
, получим значение скорости  .
.
2) Полное ускорение 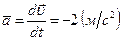 – ускорение постоянно по величине, а знак «–» указывает, что движение машины замедленное (модуль скорости уменьшается).
– ускорение постоянно по величине, а знак «–» указывает, что движение машины замедленное (модуль скорости уменьшается).
Тангенциальное ускорение 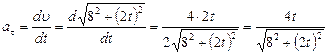 .
.
При 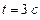 ,
, 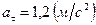 .
.
По 1.3.4 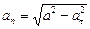 , получим в момент времени
, получим в момент времени 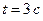
 .
.
3) Радиус кривизны окружности по 1.3.3 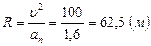 .
.
 Ответ:
Ответ: 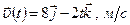 ,
, 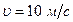 ,
, 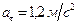 ,
, 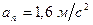 ,
, 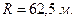
Если ускорение тела не зависит от времени и остается постоянным в процессе движения 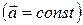 , то движение называется равнопеременным (при этом
, то движение называется равнопеременным (при этом  и траектория движения не обязательно прямолинейная).
и траектория движения не обязательно прямолинейная).
|
|
|
При равнопеременном движении скорость 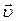 тела изменяется с течением времени по закону
тела изменяется с течением времени по закону
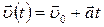 , (1.3.5)
, (1.3.5)
где 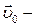 скорость в начальный момент времени.
скорость в начальный момент времени.
В свою очередь, зависимость 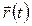 имеет вид:
имеет вид:
 , (1.3.6)
, (1.3.6)
где 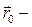 начальный радиус-вектор тела.
начальный радиус-вектор тела.
Величины 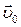 и
и  представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы
представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы 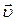 и
и 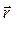 .
.
При координатном способе описания равнопеременного движения векторным уравнениям 1.3.5 и 1.3.6 соответствуют следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы координат:
 (1.3.7)
(1.3.7) 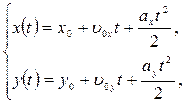 (1.3.8)
(1.3.8)
где  и
и  начальные абсцисса и ордината тела при
начальные абсцисса и ордината тела при  ,
,  и
и 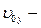 проекции
проекции
начальной скорости  тела на координатные оси,
тела на координатные оси,  и
и  проекции вектора ускорения на оси
проекции вектора ускорения на оси 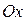 и
и 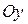 соответственно. В принципе, формулы 1.3.5 и 1.3.6 или равносильные им системы 1.3.7 и 1.3.8 позволяют решить любую задачу на движение тела с постоянным ускорением.
соответственно. В принципе, формулы 1.3.5 и 1.3.6 или равносильные им системы 1.3.7 и 1.3.8 позволяют решить любую задачу на движение тела с постоянным ускорением.
Наглядным примером равнопеременного движения является движение тела в поле тяготения Земли. Для решения задач в этом случае надо заменить в формулах 1.3.7 и 1.3.8 ускорение 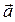 на ускорение свободного падения
на ускорение свободного падения 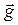 , сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяготения Земли.
, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяготения Земли.
Примечание: во всех примерах, если в условиях не оговорено иное, будем считать ускорение свободного падения  равным
равным 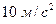 .
.
 Пример 1.3.3. Стрела выпущена из лука вертикально вверх с башни высотой
Пример 1.3.3. Стрела выпущена из лука вертикально вверх с башни высотой  со скоростью
со скоростью  . У основания башни находится ров глубиной
. У основания башни находится ров глубиной 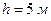 . Пренебрегая сопротивлением воздуха, определить: время подъема
. Пренебрегая сопротивлением воздуха, определить: время подъема 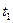 на максимальную высоту и максимальную высоту подъема
на максимальную высоту и максимальную высоту подъема 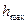 ; время полета
; время полета  стрелы до падения на дно рва, скорость
стрелы до падения на дно рва, скорость 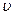 стрелы в момент падения и путь, который пролетела стрела за это время.
стрелы в момент падения и путь, который пролетела стрела за это время.
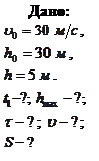
 Решение:
Решение:
Поскольку движение происходит только в вертикальном направлении, то достаточно одной координатной оси  .
.
Совместим начало отсчета с точкой нахождения лука (рис. 1.3.2).

 Начальные условия движения стрелы:
Начальные условия движения стрелы:
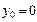 ,
, 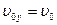 .
.
Проекция ускорения стрелы на ось 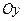 в отсутствии сопротивления воздуха равна
в отсутствии сопротивления воздуха равна  , т.к. вектор
, т.к. вектор  направлен вертикально вниз противоположно направлению координатной оси.
направлен вертикально вниз противоположно направлению координатной оси.
Вторые уравнения систем 1.3.7 и 1.3.8 с учетом начальных условий имеют вид: 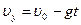 и
и 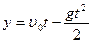 .
.
|
|
|
Пусть при 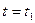 стрела находится в наивысшей точке подъема. Это значит, что
стрела находится в наивысшей точке подъема. Это значит, что 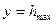 и
и 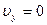 (стрела из точки 0 будет подниматься вверх до тех пор, пока ее скорость не станет равной нулю).
(стрела из точки 0 будет подниматься вверх до тех пор, пока ее скорость не станет равной нулю).
Получаем  откуда
откуда 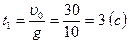 и
и 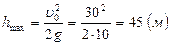 .
.
Пусть при 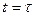 стрела упала в ров. В этот момент
стрела упала в ров. В этот момент 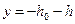 и уравнение движения имеет вид:
и уравнение движения имеет вид:
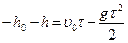 .
.
Откуда для  получаем
получаем 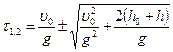 , где первое слагаемое – время подъема, второе – время падения. Отрицательный корень физического смысла не имеет, следовательно, время полета стрелы
, где первое слагаемое – время подъема, второе – время падения. Отрицательный корень физического смысла не имеет, следовательно, время полета стрелы
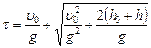
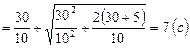 .
.
Уравнение 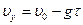 с учетом найденного значения
с учетом найденного значения  имеет вид
имеет вид
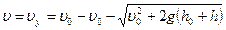

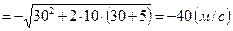 ,
,
т.е. скорость стрелы в момент падения направлена вертикально вниз – ее проекция на 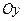 отрицательна.
отрицательна.
Путь 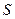 , пройденный стрелой за время полета, складывается из двух участков: подъема до высшей точки траектории и падения с высшей точки траектории в ров:
, пройденный стрелой за время полета, складывается из двух участков: подъема до высшей точки траектории и падения с высшей точки траектории в ров:
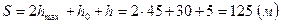 .
.
Ответ: 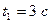 ;
; 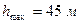 ;
; 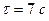 ;
; 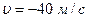 ;
;  .
.
Пример 1.3.4. Два тела брошены вертикально вверх с поверхности земли из одной точки вслед друг за другом с интервалом времени  , с одинаковыми начальными скоростями
, с одинаковыми начальными скоростями  . Пренебрегая сопротивлением воздуха, определить, через сколько времени они
. Пренебрегая сопротивлением воздуха, определить, через сколько времени они
«встретятся»? Прокомментировать решение для  .
.
 Дано: Решение:
Дано: Решение:

 Направим ось
Направим ось 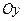 вертикально вверх, начало отсчета поместим в точку бросания. Отсчет времени будем вести с момента бросания первого тела. Начальные условия движения тел: 1)
вертикально вверх, начало отсчета поместим в точку бросания. Отсчет времени будем вести с момента бросания первого тела. Начальные условия движения тел: 1) 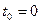 ,
,  ,
,  ; 2)
; 2) 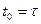 ,
, 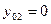 ,
,  . Проекции ускорений тел при отсутствии сопротивления воздуха равны:
. Проекции ускорений тел при отсутствии сопротивления воздуха равны: 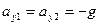 . Уравнения движения тел в проекциях на ось
. Уравнения движения тел в проекциях на ось 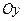 с учетом начальных условий имеют вид:
с учетом начальных условий имеют вид: 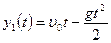 ,
, 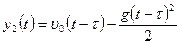 .
.
Условие «встречи»: 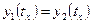 , то есть
, то есть 
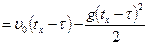 .
.
Решая это уравнение относительно  , находим
, находим  .
.
Проанализируем полученное выражение при  .
.
Время полета тела, брошенного вертикально (пример 1.3.3) вверх, до наивысшей точки подъема равно 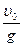 , т.е. общее время полета равно
, т.е. общее время полета равно 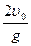 . Если
. Если  , то
, то 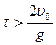 . Это означает, что сначала упадет на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания.
. Это означает, что сначала упадет на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания.
Ответ: 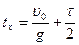 .
.
 Пример 1.3.5. Мяч бросили с башни высотой
Пример 1.3.5. Мяч бросили с башни высотой 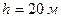 над поверхностью земли, сообщив ему начальную скорость
над поверхностью земли, сообщив ему начальную скорость  , направленную горизонтально. Пренебрегая сопротивлением воздуха, определить 1) время полета
, направленную горизонтально. Пренебрегая сопротивлением воздуха, определить 1) время полета  мяча до его падения на землю; 2) дальность
мяча до его падения на землю; 2) дальность  полета мяча; 3) скорость
полета мяча; 3) скорость 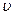 мяча в момент падения; 4) радиус
мяча в момент падения; 4) радиус 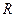 кривизны траектории мяча через
кривизны траектории мяча через 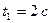 после начала движения.
после начала движения.
|
|
|
 Дано: Решение:
Дано: Решение:

 Направим оси прямоугольной системы координат так, как показано на рис. 1.3.3. Начало отсчета поместим на поверхности земли под точкой бросания. Начальные условия:
Направим оси прямоугольной системы координат так, как показано на рис. 1.3.3. Начало отсчета поместим на поверхности земли под точкой бросания. Начальные условия:
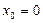 ,
,  ,
, 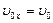 ,
, 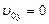 .
.
Проекции ускорения мяча на оси координат при отсутствии сопротивления воздуха равны:
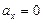 ,
,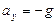 .
.
Запишем системы уравнений 1.3.7 и 1.3.8 с учетом этих значений:
 (1)
(1) 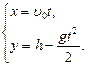 (2)
(2)
Пусть при 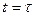 мяч упал на землю. Это означает, что
мяч упал на землю. Это означает, что 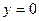 ,
, 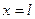 и уравнения системы (2) принимают вид:
и уравнения системы (2) принимают вид:  Решая их, находим
Решая их, находим 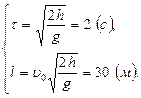
В момент падения на землю система уравнений (1) принимает вид: 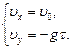
С учетом найденного значения  получим
получим 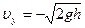 , следовательно, скорость мяча в момент падения на землю будет равна:
, следовательно, скорость мяча в момент падения на землю будет равна:
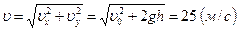 .
.
Направление вектора скорости в любой момент времени определяется углом  , который вектор
, который вектор 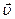 составляет с горизонтом, причем
составляет с горизонтом, причем
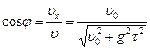 .
.
Полное ускорение при движении мяча в поле тяготения Земли всегда равно 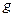 и направлено вертикально вниз. Поэтому
и направлено вертикально вниз. Поэтому  .
.
Из рис. 1.3.3 видно, что 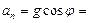
 . Учитывая, что
. Учитывая, что 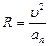 , а полная скорость
, а полная скорость 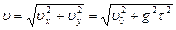 , находим радиус кривизны траектории в любой момент времени:
, находим радиус кривизны траектории в любой момент времени: 
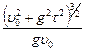 .
.
В момент времени 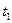 после начала движения
после начала движения 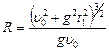
 .
.
Ответ: 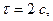
 ,
, 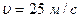 ,
,  .
.
Пример 1.3.6. Снаряд выпущен из пушки с начальной скоростью  под углом
под углом 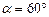 к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время подъема снаряда на максимальную высоту
к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время подъема снаряда на максимальную высоту 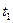 ; 2) наибольшую высоту подъема снаряда
; 2) наибольшую высоту подъема снаряда 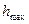 ; 3) дальность полета снаряда
; 3) дальность полета снаряда 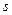 ; 4) время полета
; 4) время полета  до момента падения снаряда на землю; 5) скорость
до момента падения снаряда на землю; 5) скорость 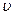 в момент его падения на землю; 6) радиус
в момент его падения на землю; 6) радиус 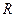 кривизны траектории снаряда в ее наивысшей точке; 7) уравнение траектории снаряда.
кривизны траектории снаряда в ее наивысшей точке; 7) уравнение траектории снаряда.
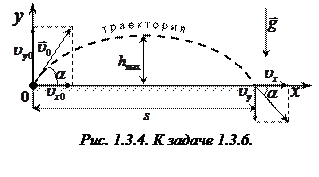
 Решение:
Решение:
 Направим оси прямоугольной системы координат так, как показано на рис. 1.3.4. Начало отсчета
Направим оси прямоугольной системы координат так, как показано на рис. 1.3.4. Начало отсчета 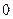 поместим в точку бросания. Начальные условия движения снаряда таковы:
поместим в точку бросания. Начальные условия движения снаряда таковы:
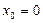 ,
, 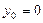 ,
, 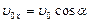 ,
,  .
.
При отсутствии сопротивления воздуха  ,
,  . С учетом этих значений системы уравнений 1.3.7 и 1.3.8 примут вид:
. С учетом этих значений системы уравнений 1.3.7 и 1.3.8 примут вид:
 (1)
(1) 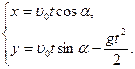 (2)
(2)
Пусть при 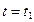 снаряд достиг максимальной высоты. В этот момент
снаряд достиг максимальной высоты. В этот момент  ,
, 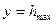 .
.
Тогда вторые уравнения обеих систем примут вид:
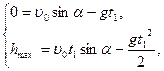 откуда
откуда 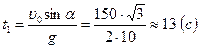 ,
,
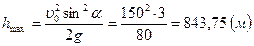 .
.
Пусть при 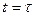 снаряд упал на землю. В этот момент
снаряд упал на землю. В этот момент 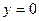 ,
,  .
.
Тогда система (2) будет иметь вид:  откуда
откуда
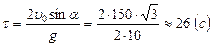 и
и  .
.
Скорость снаряда в любой момент времени равна 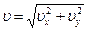 . Учитывая, что в момент падения на землю система (1) примет вид
. Учитывая, что в момент падения на землю система (1) примет вид
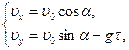 подставим в нее найденное значение
подставим в нее найденное значение  :
: 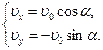
Таким образом, скорость снаряда в момент падения его на землю будет равна
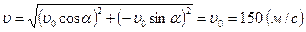 .
.
Радиус кривизны траектории снаряда в наивысшей точке траектории 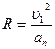 , где
, где  скорость в наивысшей точке траектории. Учитывая, что в наивысшей точке траектории
скорость в наивысшей точке траектории. Учитывая, что в наивысшей точке траектории 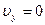 и
и  , получаем
, получаем 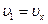 и
и
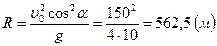 .
.
Уравнение траектории можно получить, исключив из системы (2) время 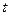 :
:
 .
.
График траектории представляет собой участок параболы, ветви которой направлены вниз.
Ответ: 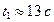 ,
, 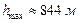 ,
, 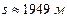 ,
,  ,
,  ,
,  ,
,  .
.

|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1067; Нарушение авторских прав?; Мы поможем в написании вашей работы!