
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения импульса. Центр масс системы
|
|
|
|
Совокупность материальных точек и тел, рассматриваемых как единое целое, называется механической системой.
Силы взаимодействия между материальными точками механической системы называют внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называют внешними. Механическая система тел, на которую не действуют внешние силы, называют замкнутой (изолированной).
Рассмотрим механическую систему, состоящую из  тел, масса и скорость которых соответственно равны
тел, масса и скорость которых соответственно равны  и
и 
Пусть  равнодействующая всех приложенных к данному телу внутренних сил,
равнодействующая всех приложенных к данному телу внутренних сил, 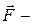 равнодействующая приложенных к данному телу внешних сил. Запишем второй закон Ньютона для каждого из
равнодействующая приложенных к данному телу внешних сил. Запишем второй закон Ньютона для каждого из  тел механической системы:
тел механической системы:
 .
.
Сложим почленно эти уравнения:
 .
.
Согласно третьему закону Ньютона силы, действующие между телами системы,
равны и противоположно направлены, поэтому геометрическая сумма внутренних сил равна нулю и 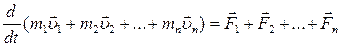 .
.
Векторная сумма импульсов тел, входящих в систему, 

 , называется импульсом системы. Таким образом,
, называется импульсом системы. Таким образом,
 (2.5.1)
(2.5.1)
Следовательно, закон изменения импульса гласит: скорость изменения импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В замкнутой системе 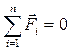 , поэтому
, поэтому 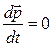 и, следовательно,
и, следовательно, 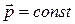 .
.
Последнее выражение является законом сохранения импульса: импульс замкнутой системы есть величина постоянная, т.е. не изменяется с течением времени.
Хотя закон сохранения импульса получен как следствие законов Ньютона, он справедлив не только в классической физике, но и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). В силу своей универсальности закон сохранения импульса является фундаментальным законом природы. Отметим, что импульс сохраняется и для незамкнутой системы, если геометрическая сумма внешних сил равна нулю.
|
|
|
Задачу на закон сохранения импульса рекомендуется решать по следующему алгоритму:
1. Сделать чертеж. На чертеже указать направление скорости движения тел, входящих в систему.
2. Записать закон сохранения импульса в векторной форме 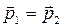 , где
, где  импульс системы тел до взаимодействия,
импульс системы тел до взаимодействия,  импульс системы тел после взаимодействия.
импульс системы тел после взаимодействия.
3. Выбрать направление координатных осей Ох и Оу и спроецировать на них записанное ранее векторное уравнение.
4. Решить полученное уравнение (систему уравнений).
 |
Пример 2.5.1. На железнодорожной платформе, движущейся по инерции со скоростью 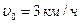 , укреплено орудие. Масса платформы с орудием
, укреплено орудие. Масса платформы с орудием  . Ствол орудия направлен в сторону движения платформы. Снаряд массой
. Ствол орудия направлен в сторону движения платформы. Снаряд массой 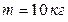 в
в  ылетает из ствола под углом
ылетает из ствола под углом  к горизонту. Определите скорость
к горизонту. Определите скорость 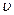 снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в
снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в 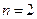 раза.
раза.

 Решение:
Решение:
 По закону сохранения импульса
По закону сохранения импульса  . В проекции на ось Ох, расположенную горизонтально (рис. 2.5.1), получаем:
. В проекции на ось Ох, расположенную горизонтально (рис. 2.5.1), получаем:  , откуда
, откуда  и
и  .
.
Ответ:  .
.

В классической механике Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс.
Центром масс системы (или центром инерции) называется воображаемая точка C, положение которой характеризуется распределением масс этой системы.
Ее радиус-вектор равен:
 , (2.5.2)
, (2.5.2)
где  и
и  масса и радиус-вектор
масса и радиус-вектор  -ой материальной точки, входящей в систему,
-ой материальной точки, входящей в систему,
 число материальных точек,
число материальных точек, 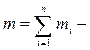 масса системы. Учитывая, что
масса системы. Учитывая, что 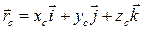 , координаты центра масс системы
, координаты центра масс системы
 ,
, 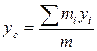 ,
,  . (2.5.3)
. (2.5.3)
Скорость центра масс системы 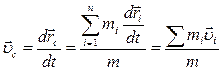 .
.
Учитывая, что  , а
, а 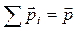 , где
, где 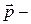 импульс системы,
импульс системы,
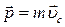 .
.
Таким образом, импульс системы равен произведению массы системы на скорость ее центра масс. Подставим это выражение во второй закон Ньютона:
 .
.
Следовательно, центр масс движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует результирующая внешних сил, приложенных к системе.
|
|
|
Для замкнутой системы 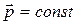 , следовательно,
, следовательно, 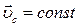 . Таким образом, центр масс замкнутой системы либо движется прямолинейно и равномерно, либо покоится(теорема о движении центра масс).
. Таким образом, центр масс замкнутой системы либо движется прямолинейно и равномерно, либо покоится(теорема о движении центра масс).
 Пример 2.5.2. Шесть маленьких шариков массами
Пример 2.5.2. Шесть маленьких шариков массами  ,
, 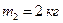 ,
, 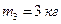 ,
, 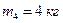 ,
, 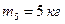 и
и  закреплены на невесомом стержне на равных расстояниях
закреплены на невесомом стержне на равных расстояниях  друг от друга. На каком расстоянии от середины стержня находится центр масс системы?
друг от друга. На каком расстоянии от середины стержня находится центр масс системы?
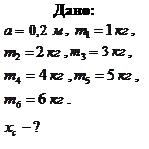
 Решение:
Решение:
Поместим начало координат в центр стержня.
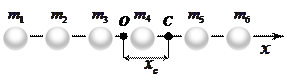

Координата центра масс (по формуле 2.5.3):
 .
.
Координаты шариков равны:


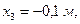
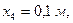

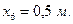
Следовательно,  .
.
Ответ: 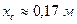 .
.
Пример 2.5.3. Материальные точки массой  каждая расположены в
каждая расположены в 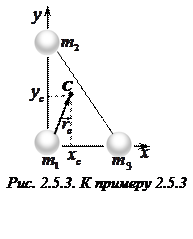 вершинах треугольника со сторонами
вершинах треугольника со сторонами 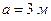 ,
,  и
и 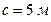 . Найти положение центра масс системы.
. Найти положение центра масс системы.

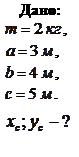 Решение:
Решение:
 Введем систему координат. Начало координат совместим с одной из точек. Данный треугольник является прямоугольным (рис. 3.5.3). Частица
Введем систему координат. Начало координат совместим с одной из точек. Данный треугольник является прямоугольным (рис. 3.5.3). Частица  имеет координаты
имеет координаты 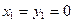 , частица
, частица 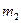 имеет координаты
имеет координаты 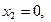
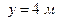 , частица
, частица  имеет координаты
имеет координаты  .
.
Координаты центра масс (по формуле 2.5.3)
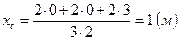 ,
, 
Ответ: координаты точки  .
.
Пример 2.5.4. Определить положение центра масс од 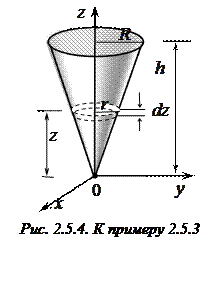 нородного конуса высотой
нородного конуса высотой  .
.

 Решение:
Решение:
 Выберем систему координат так, чтобы начало отсчета совпадало с вершиной конуса, а ось
Выберем систему координат так, чтобы начало отсчета совпадало с вершиной конуса, а ось  была направлена вдоль оси симметрии. При этом
была направлена вдоль оси симметрии. При этом 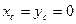 . Центр масс будет располагаться на оси симметрии.
. Центр масс будет располагаться на оси симметрии.
Пусть конус имеет радиус основания 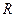 . Чтобы найти координату
. Чтобы найти координату  , разобьем конус на бесконечное число цилиндров малой высотой
, разобьем конус на бесконечное число цилиндров малой высотой  .
.
Масса каждого такого цилиндра равна 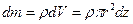 , где
, где 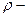 плотность вещества однородного конуса. Получаем
плотность вещества однородного конуса. Получаем  .
.
Из подобия треугольников, образованных образующей конуса, осью  и радиусами
и радиусами 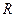 и
и  , получаем:
, получаем:  , следовательно,
, следовательно, 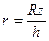 и
и  .
.
Масса конуса  , поэтому
, поэтому  .
.
 Ответ:
Ответ:  .
.
Глава 3. Работа и энергия
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1998; Нарушение авторских прав?; Мы поможем в написании вашей работы!