Четность перестановок

Дискриминантом называется многочлен от n переменных . Квадрат дискриминанта является симметрическим многочленом. Следовательно, при перестановке переменных может меняться только знак дискриминанта.

Определение 4.4. Перестановка f называется четной, если она не меняет знак дискриминанта (то есть 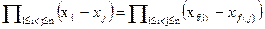), и нечетной в противном случае.

Свойство 4.4. Четность произведения перестановок зависит от четности сомножителей. Произведение перестановок одинаковой четности всегда четно, а произведение перестановок разной четности – нечетно.

Выполнение перестановки сводится к последовательному выполнению перестановок сомножителей. Следовательно, знак перестановки равен произведению знаков сомножителей.

Определение 4.5. Перестановка, меняющая только два соседних по порядку номера, называется инверсией. Инверсия имеет вид (i-i+1).

Свойство 4.5. Инверсия является нечетной перестановкой.

Применив инверсию к дискриминанту, видим, что поменяется знак только у единственного сомножителя 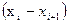. Следовательно, дискриминант меняет знак.

Определение 4.6. Для перестановки f определим число нарушений порядка как число всех пар, для которых i<j и f(i)>f(j).

Например, при 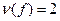так как существуют только две пары на которых нарушается порядок. Это 1,2 (f(1)=3>f(2)=1) и 1,3 (f(1)>f(3)=2).

Теорема 4.1.Перестановка f представима в виде произведения инверсий.

Доказательство проведем индукцией по
. Для существует единственная перестановка 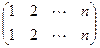. Если 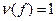, то перестановка сама является инверсией. Пусть утверждение теоремы верно при 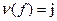. Покажем его справедливость при 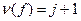. Найдем номер i для которого f(i)>f(i+1) (существование такого i очевидно). Перестановка (i-i+1)f имеет j нарушений порядка. По предположению индукции, эта перестановка представима в виде произведения j инверсий . Из полученного равенства, умножив слева на (i-i+1), находим 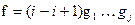. Перестановка f представлена в виде произведения j+1 инверсий, тем самым теорема доказана.

Из теоремы вытекает, что четность перестановки совпадает с четностью числа нарушений порядка в ней.

Определение 4.7. Перестановка, меняющая только два элемента, называется транспозицией.

Лемма 4.2. Транспозиция является нечетной перестановкой.

Рассмотрим транспозицию (i-j), где i<j. Число нарушений порядка этой транспозиции равно 2(j-i)-1, всегда нечетное число.

Лемма 4.3. Четность цикла длины k равна четности числа k-1.

Доказательство проведем индукцией по длине цикла k. При k=2 утверждение доказано в предыдущей лемме. Пусть утверждение леммы верно при k-1. Покажем его справедливость для цикла длины k. Из равенства следует, что четность цикла длины k равна четности цикла длины k-1 плюс 1, то есть четности k-1.

Определение 4.8. Сумма длин независимых циклов минус количество циклов называется декрементом перестановки.

Разложив перестановку в произведение независимых циклов, определим её чётность.

Теорема 4.2. Четность перестановки равна ее декременту.

Дата добавления: 2014-01-20