Свойства определителя

Разберем свойства определителей.

Замену строк матрицы на ее столбцы назовем операцией транспонирования и обозначим через .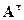

Свойство 5.1. Определитель матрицы не меняется при ее транспонировании.

Доказательство. 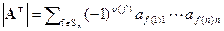. Упорядочив сомножители в каждом слагаемом по возрастанию номеров строк, получим 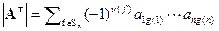, где g обратная перестановка к f. Поскольку их произведение четная перестановка, то четность f и g совпадают и 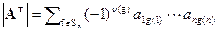. Когда f пробегает все перестановки, то g пробегает все перестановки. От перестановки слагаемых сумма не меняется, поэтому .

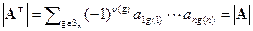Свойство 5.2. При перестановке двух строк определитель матрицы изменит знак.

Доказательство. Пусть матрица B получена из матрицы A перестановкой строк с номерами I и j. Транспозицию (i-j) обозначим через 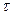. Имеет место равенство 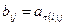. Выразим определитель матрицы B через элементы матрицы A 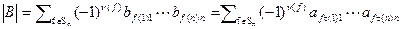. Учитывая равенство 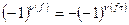и тот факт, что когда f пробегает всё множество перестановок 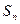, то 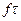тоже пробегает все множество перестановок выводим требуемое свойство.

Свойство 5.3. Если матрица имеет две одинаковые строки, то ее определитель равен 0.

Доказательство. При перестановке одинаковых строк матрица не меняется, а значит, не изменится её определитель. По доказанному ранее, определитель должен поменять знак. Выполнение этих условий возможно в единственном случае, определитель равен нулю.

Свойство 5.4. Определитель не изменится, если к строке прибавить другую строку умноженную на число.

Доказательство. Пусть матрица B получена из матрицы A прибавлением к строке i строки j, умноженной на число c. Выразим определитель матрицы B через элементы матрицы A 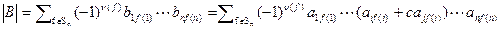. Раскроем скобки и переставим слагаемые, получим 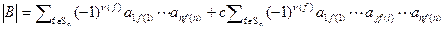. Сумма 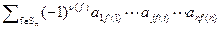является определителем матрицы, у которой две строки равны (I и j), и, значит, равна нулю. Таким образом, .

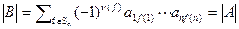Свойство 5.5. Определитель треугольной матрицы равен произведению диагональных элементов.

Доказательство. Пусть матрица A имеет верхнее треугольный вид, т.е 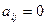при i<j. Определитель матрицы равен 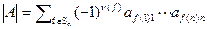. Если 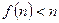, то 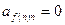, поэтому в сумме ненулевое слагаемое только при 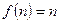. Поскольку 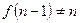, то аналогично рассуждая, получаем 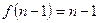. И так далее. В результате, сумма содержит только одно ненулевое слагаемое, соответствующее тожественно перестановке, и, значит 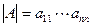. Если матрица имеет нижнее треугольный вид, то транспонированием приведём её к верхнее треугольному виду, а потом применим Свойство 5.5.

Поскольку при транспонировании определитель матрицы не меняется, а преобразования со строками становятся преобразованиями со столбцами, то тем самым установлено

Свойство 5.6 Определитель матрицы

1. изменит знак при перестановке столбцов

2. равен нулю, если имеется два одинаковых столбца

3. не изменится при прибавлении к столбцу другого столбца, умноженного на число.

Дата добавления: 2014-01-20