Формула полной вероятности

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса.

Пусть событие А может наступить при условии появления одного из несовместных событий Н ₁, Н ₂,…, Н_n, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности Р (А / Н ₁), Р (А / Н ₂), …,Р (А / Н_n) события А. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий Н ₁, Н ₂,…, Н_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р (А) = Р (Н ₁) Р (А / Н ₁) + Р (Н ₂) Р (А / Н ₂) +...... + Р (Н_n) Р (А / Н_n) = 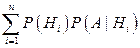.(3.6)

Формулу (3.6) называют «формулой полной вероятности».

Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий Н ₁, Н ₂,…, Н_n. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий Н ₁ А, Н ₂ A,..., Н_nА. Пользуясь для вычисления вероятности события А теоремой сложения, получим

Р (А) = Р (Н ₁ А) + Р (Н ₂ А) +...... + Р (Н_nА). (3.7)

Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем

Р (Н ₁ А) = Р (Н ₁) Р (А / Н ₁); Р (Н ₂ А) = Р (Н ₂) Р (А / Н ₂);…, Р (Н_nА) = Р (Н_n) Р (А / Н_n).

Подставив правые части этих равенств в соотношение (3.7), получим формулу полной вероятности

Р (А) = Р (Н ₁) Р (А / Н ₁) + Р (Н ₂) Р (А / Н ₂)+...... + Р (Н_n) Р (А / Н_n).

Отметим, что в формуле (3.6) события Н ₁, Н ₂,…, Н_n обычно называют гипотезами; они исчерпывают все возможные предположения (гипотезы) относительно исходов как бы первого этапа опыта, событие А – один из возможных исходов второго этапа.

Пример. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.

Решение. Обозначим через А событие «извлеченная деталь стандартна». Деталь может быть извлечена либо из первого набора (событие Н ₁), либо из второго (событие Н ₂). Вероятность того, что деталь вынута из первого набора, Р (Н ₁) = 1/2. Вероятность того, что деталь вынута из второго набора, Р (Н ₂) = 1/2. Условная вероятность того, что из первого набора будет извлечена стандартная деталь, Р (А / Н ₁) = 0,8. Условная вероятность того, что из второго набора будет извлечена стандартная деталь, Р (А / Н ₂) = 0,9.

Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна

Р (А) = Р (Н ₁) Р (А / Н ₁) + Р (Н ₂) Р (А / Н ₂) = 0,5•0,8 +0,5 0,9 = 0,85.

Пример. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.

Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа». Из второй коробки могла быть извлечена либо стандартная лампа (событие Н ₁), либо нестандартная (событие Н ₂).

Вероятность того, что из второй коробки извлечена стандартная лампа, Р (Н ₁) =9/10. Вероятность того, что из второй коробки извлечена нестандартная лампа, Р (Н ₂) = 1/10.

Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна Р (А / Н ₁) = 19/21. Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна Р (А / Н ₂) = 18/21.

Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна

.

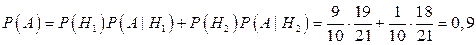Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Решение. Вероятность того, что выстрелы производит первый, второй или третий стрелок равна 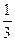. Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка:

- для второго стрелка: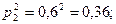

- для третьего стрелка:

Искомая вероятность равна:

.

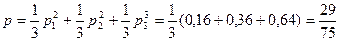Пример. Из урны, содержащей 3 белых и 2 черных шара, наугад вынимают 2 шара и перекладывают в другую урну, содержащую 4 белых и 4 черных шара. Какова вероятность вынуть белый шар при случайном выборе одного шара из второй урны после перекладывания?

Решение. Эта задача решается обычно с помощью формулы полной вероятности. Пусть А – событие, означающее отбор белого шара. Определим полную группу событий в соответствии с возможными результатами перекладывания: H ₁ = {Б, Б}, H ₂ = {Б, Ч} + {Ч, Б}, H ₃ = {Ч, Ч}. Здесь первая буква в фигурных скобках указывает цвет шара, который был вынут из первой урны, а вторая буква – цвет второго шара. Термин «наугад» означает, что вероятность вынкть шар определенного цвета равна отношению числа шаров этого цвета к общему числу шаров в урне. В таком случае, в соответствии с формулой условной вероятности, Р (второй шар белый | первый шар белый)× Р (первый шар белый) 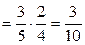. Аналогично, 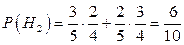и . Условные вероятности события А вычисляются в соответствии с числом белых шаров во второй урне после добавления в нее двух шаров из первой урны: Р (А / Н ₁) = 6/10, Р (А / Н ₂) = 5/10, Р (А / Н ₃) = 4/10. Формула полной вероятности дает

.

Замечание. Следует обратить особое внимание на пространство W элементарных исходов в этой задаче, - ошибочно считать, что W имее всего два элемента Б и Ч. Наш эксперимент состоял не только в отборе шара из второй урны – перед этим производился слычайный отбор бвух шаров из первой урны, и результат этого отбора влиял на условную вероятность выбора белого шара. Пространство W в действительности состоит из восьми элементов

ББ.Б БЧ.Б ЧБ.Б ЧЧ.Б

ББ.Ч БЧ.Ч ЧБ.Ч ЧЧ.Ч

Здесь первые две буквы до точки указывают цвет шаров, вынутых из первой урны, а буква после точки – цвет шара, вынутого из второй урны после перекладывания. Вычисления, проводимые в таком пространстве W, представляют собой суммирование вероятностей элементарных исходов, указанных в первой строке.

Следующая задача иллюстрирует недоразумения, которые могут возникнуть из-за неправильной спецификации пространства элементарных исходов.

Пример. Экспериментатор располагает двумя парами шаров одинакового цветового состава БЧ и БЧ. Из каждой пары наугад выбирается по одному шару и бросается в урну, где лежит белый шар. Из трех шаров в урне наугад отбирается один. какова веротяность того, что вынут белый шар?

Решение. Снова находимся в ситации, связанной с применением флормулы полной вероятности, где полная группа событий соотносится с возможным составом урны: H ₁ = БББ (в урне 3 белых шара), H ₂ = ББЧ + БЧБ (в урне 2 белых), H ₃ = БЧЧ (в урне 1 белый). Поскольку вероятность выбора шара определенного цвета из каждой пары равна 1/2 и выбор в каждой паре осуществляется независимо от результата выбора в другой, то вероятности событий из полной группы вычисляются просто: , 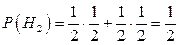. Условные вероятности отбора белого шара при каждом фиксированном составе урны равны Р (А / Н ₁) = 1, Р (А / Н ₂) = 2/3, Р (А / Н ₃) = 1/3. Теперь, используя формулу полной вероятности, находим 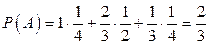. Если игнорировать процесс случайного формирования состава урны и считать, что мы имеем дело с двухточечным пространством элементарных исходов W = {Б, Ч}, то приходим к парадоксальному выводу: состав урны всегда один и тот же – два белых и один черный!

Нетрудно понять, что в этой задаче пространство элементарных исходов то же, что и в предыдущей задаче (дополнительный белый шар фиксирован и его можно не учитывать при определении W), и наши вычисления Р (А) состоят в суммировании вероятностей элементарных исходов первой строки в таблице, представляющей пространство W.

Дата добавления: 2014-01-20