Свойства математического ожидания

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

М (С) = С.

Доказательство. Будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью р = 1. Следовательно,

М (С) = С× 1 = C.

Замечание. Определим произведение постоянной величины С на дискретную случайную величину X как дискретную случайную СХ, возможные значения которой равны произведениям постоянной С на возможные значения X; вероятности возможных значений СХ равны вероятностям соответствующих возможных значений X. Например, если вероятность возможного значения х ₁ равна p ₁, то вероятность того, что величина СХ примет значение Cx ₁, также равна р ₁.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

М (СХ) = СМ (X).

Доказательство. Пусть случайная величина X задана законом распределения вероятностей:

X	x 1	x 2	…	хn
р	р 1	р 2	…	рn

Учитывая замечание 1, напишем закон распределения случайной величины СХ:

СX	Сx 1	Сx 2	…	Схn
р	р 1	р 2	…	рn

Математическое ожидание случайной величины СХ:

М (СХ) = Сx ₁ р ₁ + Сx ₂ р ₂ + …+ Сx_nр_n = С (x ₁ р ₁ + x ₂ р ₂ + …+ x_nр_n) = СМ (Х).

Итак,

М (СХ) = СМ (X).

Замечание 2. Прежде чем перейти к следующему свойству, укажем, что две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Замечание 3. Определим произведение независимых случайных величин X и Y как случайную величину XY, возможные значения которой равны произведениям каждого возможного значения X на каждое возможное значение Y; вероятности возможных значений произведения XY равны произведениям вероятностей возможных значений сомножителей. Например, если вероятность возможного значения x ₁ равна р ₁ и вероятность возможного значения у ₁ равна g₁, то вероятность возможного значения х ₁ у ₁ равна р ₁g₁.

Заметим, что некоторые произведения x_iy_j могут оказаться равными между собой. В этом случае вероятность возможного значения произведения равна сумме соответствующих вероятностей. Например, если х ₁ у ₂ = х ₃ у ₅, то вероятность х ₁ у ₂ (или, что то же, х ₃ у ₅) равна р ₁g₂ + р ₃g₅.

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M (XY) = M (X) M (Y).

Доказательство. Пусть независимые случайные величины X и Y заданы своими законами распределения вероятностей (для упрощения выкладок ограничимся малым числом возможных значений. В общем случае доказательство аналогичное):

X	x 1	x 2	Y	у 1	у 2
р	р 1	р 2	g	g1	g2

Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все возможные значения X на каждое возможное значение Y; в итоге получим х ₁ у ₁, х ₁ у ₂, х ₂ у ₁ и х ₂ у ₂. Учитывая замечание 3, напишем закон распределения XY, предполагая для простоты, что все возможные значения произведения различны (если это не так, то доказательство проводится аналогично):

XY	х 1 у 1	х 1 у 2	х 2 у 1	х 2 у 2
р	р 1g1	р 2g1	р 1g2	р 2g2

Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

,

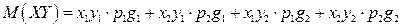или

,

Итак, M (XY) = M (X)× M (Y).

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Например, для трех случайных величин имеем:

.

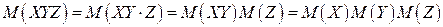Для произвольного числа случайных величин доказательство проводится методом математической индукции.

Пример. Независимые случайные величины X и Y заданы следующими законами распределения:

X				Y
p	0,6	0,1	0,3	p	0,8	0,2

Найти математическое ожидание случайной величины XY.

Решение. Найдем математические ожидания каждой из данных величин:

M (X) = 5×0,6 + 2×0,1 +4×0,3 = 4,4;

М (Y) = 7×0,7 + 9×0,2 = 7,4.

Случайные величины X и Y независимые, поэтому искомое математическое ожидание

M (XY) = M (X)× M (Y) = 4,4×7,4 = 32,56.

Замечание 4. Определим сумму случайных величин X и Y как случайную величину X + Y, возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений X + Y для независимых величин X и Y равны произведениям вероятностей слагаемых; для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

Заметим, что некоторые суммы х + у могут оказаться равными между собой. В этом случае вероятность возможного значения суммы равна сумме соответствующих вероятностей. Например, если x ₁ + y ₂ = x ₃ + y ₅ и вероятности этих возможных значений соответственно равны р ₁₂ и р ₃₅, то вероятность x ₁ + y ₂ (или, что то же, x ₃ + y ₅) равна р ₁₂ + р ₃₅.

Следующее ниже свойство справедливо как для независимых, так и для зависимых случайных величин.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

М (X + Y) = М (X) + М (Y).

Доказательство. Пусть случайные величины X и Y заданы следующими законами распределения (ограничимся лишь двумя возможными значениями каждой из величин. В общем случае доказательство аналогичное):

X	x 1	x 2	Y	у 1	у 2
р	р 1	р 2	g	g1	g2

Составим все возможные значения величины X + Y. Для этого к каждому возможному значению X прибавим каждое возможное значение Y; получим x ₁ + y ₁, x ₁ + y ₂, x ₂ + y ₂и x ₂ + y ₂. Предположим для простоты, что эти возможные значения различны (если это не так, то доказательство проводится аналогично), и обозначим их вероятности соответственно через р ₁₁, р ₁₂, р ₂₁ и р ₂₂.

Математическое ожидание величины X + Y равно сумме произведений возможных значений на их вероятности:

,

или

, (6.4)

Докажем, что р ₁₁ + р ₁₂= p ₁. Событие, состоящее в том, что X примет значение х ₁ (вероятность этого события равна р ₁), влечет за собой событие, которое состоит в том, что X + Y примет значение x ₁ + y ₁ или x ₁ + y ₂ (вероятность этого события по теореме сложения равна р ₁₁ + р ₁₂), и обратно. Отсюда и следует, что р ₁₁ + р ₁₂= p ₁. Аналогично доказываются равенства

р ₂₁ + р ₂₂= p ₂, р ₁₁ + р ₂₁= g ₁и р ₁₂ + р ₂₂= g ₂.

Подставляя правые части этих равенств в соотношение (6.4), получим

,

или окончательно

М (X + Y) = М (X) + М (Y).

Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

Например, для трех слагаемых величин имеем

.

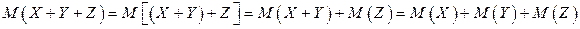Для произвольного числа слагаемых величин доказательство проводится методом математической индукции.

Пример. Производится 3 выстрела с вероятностями попадания в цель, равными p ₁ = 0,4; p ₂ = 0,3 и р ₃=0,6. Найти математическое ожидание общего числа попаданий.

Решение. Число попаданий при первом выстреле есть случайная величина x ₁, которая может принимать только два значения: 1 (попадание) с вероятностью p ₁ = 0,4 и 0 (промах) с вероятностью q = 1 – 0,4 = 0,6. Математическое ожидание числа попаданий при первом выстреле равно вероятности попадания, т.е. M (X ₁) = 0,4. Аналогично найдем математические ожидания числа попаданий при втором и третьем выстрелах: M (X ₂) = 0,3, M (X ₃) = 0,6.

Общее число попаданий есть также случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов:

X = X ₁ + X ₂ + X ₃.

Искомое математическое ожидание находим по теореме о математическом, ожидании суммы:

М (X) = M (X ₁ + X ₂ + X ₃) = M (X ₁) + M (X ₂) + M (X ₃) = 0,4 + 0,3+0,6=1,3 (попаданий).

Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение. Обозначим число очков, которое может выпасть на первой кости, через X и на второй – через Y. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5 и 6, причем вероятность каждого из этих значений равна 1/6.

Найдем математическое ожидание числа очков, которые могут выпасть на первой кости:

.

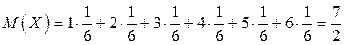Очевидно, что и М (Y) = 7/2. Искомое математическое ожидание

М (X + Y) = М (X) + М (Y) = 7/2 + 7/2 =7.

Дата добавления: 2014-01-20