Свойства функции распределения

Свойство 1. F (х) ограничена, то есть значения функции распределения принадлежат отрезку [0, 1]:

0 £ F (х) £ 1.

Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2. F (х) – неубывающая функция на R, т.е.

F (x ₂) ³ F (x ₁), если х ₂ > х ₁.

Доказательство. Пусть х ₂ > х ₁. Событие, состоящее в том, что X примет значение, меньшее х ₂, можно подразделить на следующие два несовместных события:

1) X примет значение, меньшее х ₁, с вероятностью Р (X < х ₁);

2) X примет значение, удовлетворяющее неравенству х ₁£ X < х ₂, с вероятностью Р (х ₁£ X < х ₂). По теореме сложения имеем

.

Отсюда

.

или

. (9.1)

Так как любая вероятность есть число неотрицательное, то F (x ₂) – F (x ₁) ³ 0, или F (x ₂) ³ F (x ₁), что и требовалось доказать.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

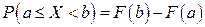. (9.2)

Это важное следствие вытекает из формулы (9.1), если положить х ₂ = b и x ₁ = a.

Рис. 9.2

Пример. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0, 2):

Р (0 < Х < 2) = F (2) – F (0).

Решение. Так как на интервале (0, 2), по условию, F (x) = x /4 + 1/4, то

Итак, Р (0< X < 2)= 1/2.

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Действительно, положив в формуле (9.2) а = х ₁, b = х ₁ + D х, имеем

.

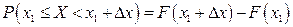Устремим D х к нулю. Так как X – непрерывная случайная величина, то функция F (x) непрерывна. В силу непрерывности F (х) в точке x ₁ разность также стремится к нулю; следовательно, Р (X = х ₁) = 0. Используя это положение, легко убедиться в справедливости равенств

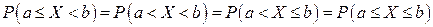(9.3)

Например, равенство 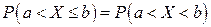доказывается так:

.

Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот фак полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство нулю вероятности Р (X = х ₁) означает, что событие X = х ₁ невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений; в частности, это значение может оказаться равным х ₁.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F (x) = 0 при х £ а; 2) F (x) = 1 при х ³ b.

Доказательство. 1) Пусть х ₁ £ а. Тогда событие X < х ₁ невозможно (так как значений, меньших х ₁, величина X по условию не принимает) и, следовательно, вероятность его равна нулю.

2) Пусть х ₂ ³ b. Тогда событие X < х ₂ достоверно (так как все возможные значения X меньше х ₂) и, следовательно, вероятность его равна единице.

Свойство 4. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

.

Свойство 5. F (x) непрерывна слева, то есть

.

Всякая функция F (x), обладающая свойствами 1 – 5, может быть функцией распределения некоторой случайной величины. Заметим, что формула (9.2) справедлива и для н.с.в., и для д.с.в.

С помощью функции распределения можно вычислить вероятность события { X ³ x }:

. (9.4)

Можно дать более точное определение н.с.в.

Определение. Случайную величину Х называют непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

Функция распределения д.с.в. имеет вид

. (9.5)

Здесь суммирование ведется по всем i, для которых x_i < x. Равенство (9.5) непосредственно вытекает из определения (*).

Дата добавления: 2014-01-20