Градиент скалярного поля потенциала. Градиентом потенциала в точке А(x,y,z) назовем производную функции U по линии, направленной в точке А вдоль вектора нормали :

Градиентом потенциала в точке А(x,y,z) назовем производную функции U по линии, направленной в точке А вдоль вектора нормали :

. (1.15)

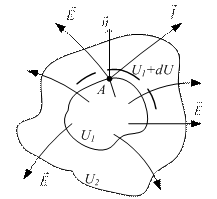
Градиент потенциала – это вектор, направленный в каждой точке перпендикулярно эквипотенциальной поверхности, т.е. в направлении вектора напряженности поля , рис. 1.4.

а) б)

Рис. 1.4. Эквипотенциальные поверхности (a), к определению градиента и
производной по направлению (б)

По абсолютной величине градиент потенциала равен скорости изменения потенциала в направлении .

Функцию называют производной по направлению.

Производные потенциала в точке А по направлению каждой из координатных осей x, y и z соответственно равны:

, ,

.

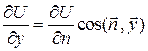Очевидно, что эти производные по направлениям x, y, z, равны проекциям градиента,

, (1.16)

где

, , .

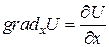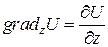По абсолютной величине

. (1.17)

На основании формулы (1.14)

, ,

и

. (1.18)

Таким образом, установлен очень важный факт, заключающийся в том, что напряженность электрического поля равна градиенту потенциала с обратным знаком. Расписывая это выражение по координатам, находим, что

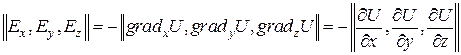, (1.19)

или

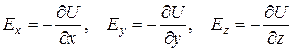. (1.20)

Учитывая, что , получим:

. (1.21)

С учетом (3.12) также получим:

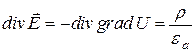, (1.22)

или

. (1.23)

Последнее уравнение называют уравнением Пуассона. В развернутом виде

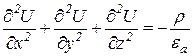. (1.24)

Если в исследуемом объеме отсутствуют заряды, то

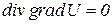, (1.25)

или

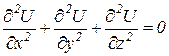. (1.26)

Это уравнение называют уравнением Лапласа.

Полученные уравнения позволяют решить следующую очень важную задачу. Как, зная распределение зарядов в некоторой области определить напряженности полей E_x, E_y, E_z в каждой точке пространства с координатами x, y, z. Из анализа выражения (1.21) следует, что решить непосредственно уравнение

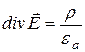
относительно трех неизвестных E_x, E_y, E_z нельзя.

Однако можно решить дифференциальные уравнения в частных производных Пуассона относительно одной неизвестной – потенциала U, а затем найти составляющие поля из формул (1.20). Что касается уравнения Лапласа, то, казалось бы, что при отсутствии зарядов его нет смысла рассматривать. Однако его решения очень важны тогда, когда можно задать граничные условия. В этом случае оно дает единственное решение для свободного пространства, если заданы значения полей на некоторой границе.

Дата добавления: 2014-01-20