Лекция №16. Отражение и преломление плоских волн на плоской границе раздела двух сред

Отражение и преломление плоских волн на плоской
границе раздела двух сред

Границу раздела двух сред считают плоской, если соотношение между неровностями ее поверхности и длиной волны удовлетворяет критерию Релея,

.

Пусть на границу раздела двух сред с электрофизическими параметрам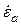и и падает плоская волна под углом 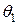. Плоский фронт падающей волны перпендикулярен направлению падения, рис. 16.1. Пусть отраженная волна движется в пока неизвестном направлении , а преломленная – в направлении .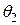

Рис. 16.1. Плоская волна на границе раздела двух сред

Пусть также волна имеет вертикальную поляризацию, т.е. вектор лежит в вертикальной плоскости .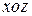

Для гармонического колебания плоскую падающую волну в комплексной форме можно записать в виде

,

,

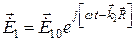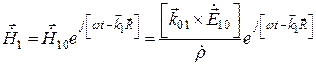где ,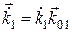

,

,

, ,

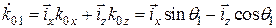– векторное произведение векторов 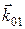и .

В выражениях (16.1), (16.2) множитель как общий для всех формул, описывающих гармонические колебания, можно опустить. Определяя волновые вектора в проекциях и, учитывая тот факт, что

,

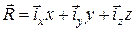запишем выражения для комплексных амплитуд полей падающей, преломленной и отраженной волн

,

,

,

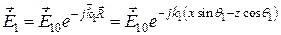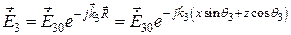где

, , ,

, , .

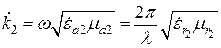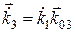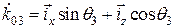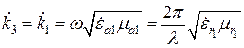Выражения в круглых скобках в экспонентах в формулах (16.4 - 16.6) с учетом знаков равны расстояниям от точек А, В, и С с текущими координатами 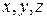до точки 0, рис. 16.1.

Магнитные компоненты полей с точностью до множителя 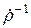также определяются формулами (16.4 - 16.6), т.е.

,

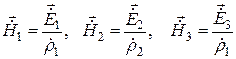где

, .

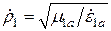Коэффициенты отражения и преломления будем находить, привлекая данные о граничных условиях.

Так на границе тангенциальные составляющие электрического и магнитного полей удовлетворяют условиям

,

.

Тогда при подстановке в (16.4 - 16.5) и учете этих граничных условий имеем:

,

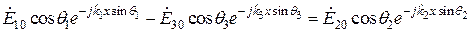Это равенство должно выполняться для любого значения 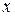. Это возможно лишь в случае, когда

.

Естественно, что из выполнения этого равенства следует выполнение такого равенства

.

Так как в верхней среде , то из (16.13) следует, что

,

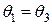т.е. угол падения равен углу отражения. Из этого же уравнения (16.13), т.е. из равенства следует, что

,

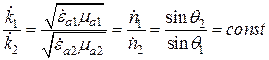где – показатель преломления среды.

Соотношения (16.15), (16.16) называют законами Снеллиуса.

Учитывая граничные условия (16.10) для магнитных компонент находим, соответствующие результирующие поля на границе. При этом также учитываем, что вектор 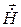перпендикулярен плоскости падения 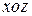и параллелен границе раздела. В соответствии с правилом правого винта, относительно направления распространения, приходим к выводу, что и в падающей, и в отраженной, и в преломленной волнах вектор 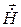направлен в одну сторону (от плоскости чертежа к читателю).

Поступая так же, как и при получении формул (16.11 - 16.14) находим, что на границе

,

или

.

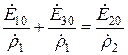Тогда имеем такую пару уравнений (совместно с (16.14))

,

,

решая которую, находим коэффициенты отражения и преломления для колебаний вертикальной поляризации

,

.

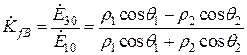Эти коэффициенты называют коэффициентами отражения и преломления Френеля.

Для определения этих коэффициентов отражения Френеля, т.е. для решения системы (16.18), (16.19), умножим уравнение (16.18) на 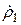, а (16.19) - на 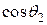. Тогда получим

,

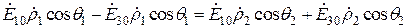или

,

.

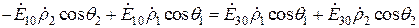Отсюда находим, что коэффициент отражения Френеля для электрических полей вертикальной поляризации равен (16.20), т.е.,

.

Пусть . Тогда учитывая, что в соответствии с (16.16)

,

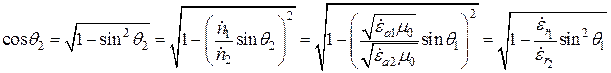находим, что

,

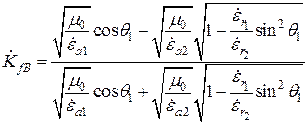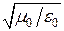т.к. , то на множитель числитель и знаменатель можно сократить. Тогда

.

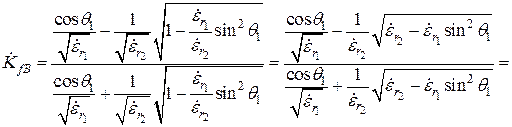
Точно также нетрудно получить формулы для коэффициентов отражения и преломления Френеля для колебаний горизонтальной поляризации

,

.

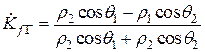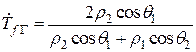В частности, при ,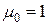

,

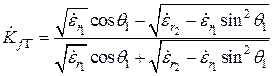при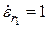

,

.

Эти коэффициенты имеют важнейшее значение при решении различных практических задач распространения радиоволн.

Зависимости модулей коэффициентов отражения Френеля от в случае чисто диэлектрической среды и среды с проводимостью показаны на рис. 16.2 и рис. 16.3 соответственно.

Рис. 16.2. Зависимости модулей коэффициентов отражения Френеля от .
Случай чисто диэлектрической среды.

Рис. 16.3. Зависимости модулей коэффициентов отражения Френеля от .
Случай среды с проводимостью.

На этих рисунках показаны графики зависимостей коэффициентов отражения для колебаний горизонтальной и вертикальной поляризаций для двух типов поверхностей с различными свойствами.

Угол, при котором коэффициент отражения волн вертикальной поляризации равен нулю, называют углом полного внутреннего преломления или углом Брюстера. При падении волн под этим углом на поверхность отраженная волна отсутствует, поле полностью уходит под поверхность и имеет место лишь преломленная волна. Величина этого угла зависит от величины диэлектрической проницаемости. Чем больше , тем больше этот угол.

Дата добавления: 2014-01-20